搅拌槽内蕴含着丰富的非稳态流体流动行为，使得槽内流体在相当大的时间和空间尺度上存在着流动形态发生随机脉动的现象，如流动信号中压力脉动信号的随机脉动。其实，静止流体受到搅拌桨旋转的激励作用而产生流动，具有随机非平稳、时频及局部特性。这种多样流动行为的存在，增加了流动信号研究的困难程度，难以为搅拌反应器内气液混合行为的认识以及工程应用与放大提供支撑。

虽然流体混沌混合具有初始敏感性，但搅拌反应器内流体被诱发进入混沌时，流场中湍流涡旋串级或碰撞以及流体多尺度结构的形成、运移和演化过程所引起的速度变化并不是瞬间的，它会影响将来的速度场，进而影响流场界面结构，造成湍流的记忆性。这一方面可以引入分数阶系统的Navier-Stokes 方程来描述流场中流体颗粒结构自转或其他颗粒间的相互作用。目前，已知的分数阶系统有分数阶Lorenz 系统、分数阶Duffing 系统、分数阶Liu 系统以及分数阶Chen 系统等，它们都可以描述流场中复杂的非线性动力学行为。对这些分数阶自治系统的研究表明，当系统的阶数低于3 阶时，体系中就存在着混沌行为。例如，对处于混沌状态的分数阶Newton-Leipnik 系统，随着阶数的下降，系统表现出逆Hopf 分岔过程，双重吸引子（见图2.5）将会突变成单吸引子（见图2.6）。对具有分数阶阻尼的Vander-Pol 系统，当阶数小于1时，系统表现出周期运动、拟周期运动以及混沌运动。分数阶Wien 电桥振荡器对某些合理的增益值，在任意分数阶次下，都能产生极限环行为。对分数阶Rössler 系统以及超Rössler 系统，当阶数分别低于2.4 和3.8 时，相应系统出现混沌以及超混沌现象（见图2.7）。这些研究结果打破了人们对经典自治系统中出现混沌现象的规律认知，同时表明，分数阶动力系统往往描述体系中较为复杂的动力学行为。

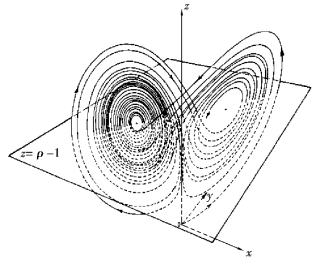
图2.5　双重吸引子

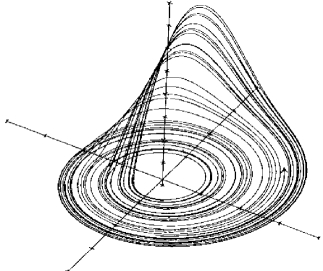
图2.6　单吸引子

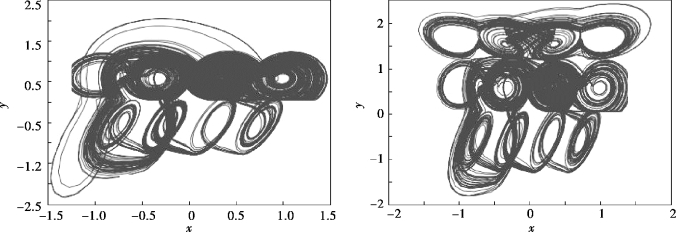
图2.7　多混沌吸引子

（1）信号处理方法

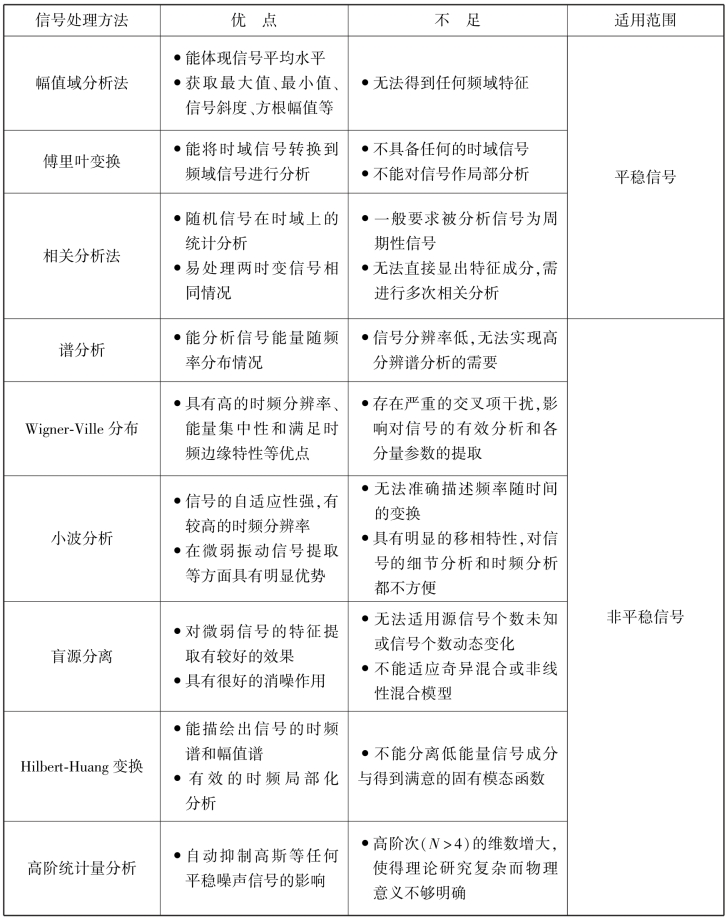
目前，关于信号特征方面的研究开展了诸多探索。信号处理的方法有很多，依据其信号的平稳性与否，大致可分为两类。对于平稳信号的处理来讲，主要包括幅值域分析法、傅里叶变换、相关分析法及谱分析。对于非稳信号的处理来讲，主要包含Wigner-Ville 分布、小波分析、盲源分离、Hilbert-Huang 变换及高阶统计量分析等。上述信号处理方法的应用范围及其优缺点见表2.1。

表2.1　各类信号处理方法的优缺点及其适用范围

（2）分数阶傅里叶变换

针对时变非平稳信号的时频局部特性，学者们提出分数阶傅里叶变换（fractional Fourier transform，FRFT）的解决方法，并利用时频平面旋转的思路对其进行物理解释。实质上，分数阶傅里叶变换具有明显的时频旋转特性，随着变换阶次从0 到1 的连续变化，能够将从时域到频域变化过程中所有特征呈现出来，它是一种介于时域与频域之间的信号分析方法（见图2.8）。自1996 年Ozaktas 等提出一种计算FRFT 的离散算法以来，FRFT 在信号领域的应用研究不断受到广大学者的关注。

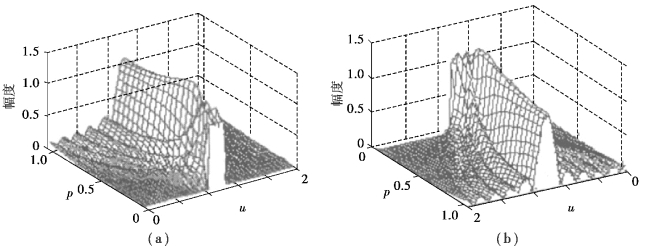
图2.8　矩形脉冲信号的分数阶傅里叶变换

分数阶傅里叶变换的定义为

其中

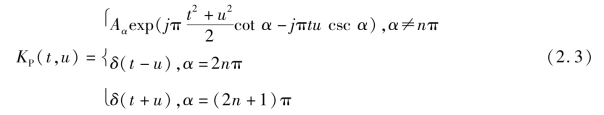
式中，α=pπ/2，p 为分数阶傅里叶变换的阶数，α 为旋转角度，f（t）为被分析的连续信号表达式，Fp（u）表示变换阶数为p 分数阶傅里叶变换形式，KP（t，u）表示分数阶傅里叶变换的核函数，t 为时间。

（3）分数阶傅里叶变换的基本性质

作为一种广义的傅里叶变换方式，分数阶傅里叶变换具有传统傅里叶变换所不具备的一些基本性质。

1）叠加性

分数阶傅里叶变换作为一种变换手段，满足叠加原理，即Hα（u）和Gα（u）分别满足函数f（t）和g（t）的分数阶傅里叶变换，则有

2）旋转相加性

函数f（t）的分数阶傅里叶变换具有旋转相加性，即

3）结合性

对于旋转角度α，β，γ 的3 个分数阶傅里叶变换来讲，即

4）连续性

对于两个旋转角度α1 和α2 的分数阶傅里叶变换来讲，有

5）自成像性(www.daowen.com)

在式（2.7）中，当令c2α=2π 时，则有

6）逆运算性质

分数阶傅里叶变换算子具有逆运算特性，即

7）酉性

数阶傅里叶变换算子具有酉性，具体表达为

8）Parseval 准则

在帕塞瓦尔准则中，设Fα（u）和Gα（u）分别表示f（t）和g（t）函数的分数阶傅里叶变换，则有

（4）分数阶傅里叶变换运算的性质

分数阶傅里叶变换运算的基本性质是其应用的基础，所谓性质是指信号在时域或分数域发生了某种运算之后，在分数域发生相应的变化规律，这些规律也有相应的物理概念。在许多通信与信号处理系统中都需要借助其性质的运用及其运算原理。

1）时间倒置特性

若Fα（u）=Fα [f（t）]（u），则

2）共轭特性

若Fα（u）=Fα [f（t）]（u），则

3）尺度变换特性

若Fα（u）=Fα [f（t）]（u），则

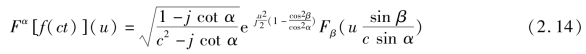
式中，β=arctan（c2tan α）。

4）时移特性

若Fα（u）=Fα [f（t）]（u），则

5）频移特性

若Fα（u）=Fα [f（t）]（u），则

6）微分特性

若Fα（u）=Fα [f（t）]（u），则

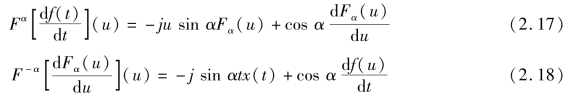
7）积分特性

若Fα（u）=Fα [f（t）]（u），则有

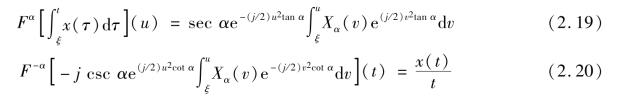
分数阶傅里叶变换是由传统傅里叶变换演变而来的，傅里叶变换的大多数性质也同样适用于分数阶傅里叶变换，详细的变换过程推导见文献[152，153]。分数阶傅里叶变换是通过角度α 在时频面的旋转，从而实现时频信号特征的提取。这种变换行为与信号的时频分布有直接关系，也是该变换实现物理意义表述的关键。正是基于以上优势，利用分数阶傅里叶变换对搅拌反应器内流动信号进行时频域内的全局及局部特征分析，以期为搅拌反应器内流体混合行为的理解提供深入的认识。