1.表达式化简的意义和最简标准

（1）表达式化简的意义

数字逻辑电路是按照表达式的运算结构连接成的，而一种逻辑功能可以有多种结构的表达式。

【例4-4】由真值表写出的或运算表达式

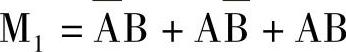
由或运算定义写出的表达式

M₂=A+B

两个表达式对应的逻辑图如图4-13所示。

前面已证明两个表达式的逻辑功能是等效的，选择结构最简单的表达式制作电路，可以提高电路运行的速度及可靠性，还能降低制作成本。因此，表达式化简是逻辑电路设计过程中不可忽视的环节。

（2）表达式最简标准

把结构复杂的表达式转换为结构最简单的表达式叫做表达式化简，也叫逻辑函数化简。与或表达式的最简标准是：乘积项个数最少；每个乘积项中的变量个数最少。

2.表达式化简方法

（1）表达式化简方法的实质

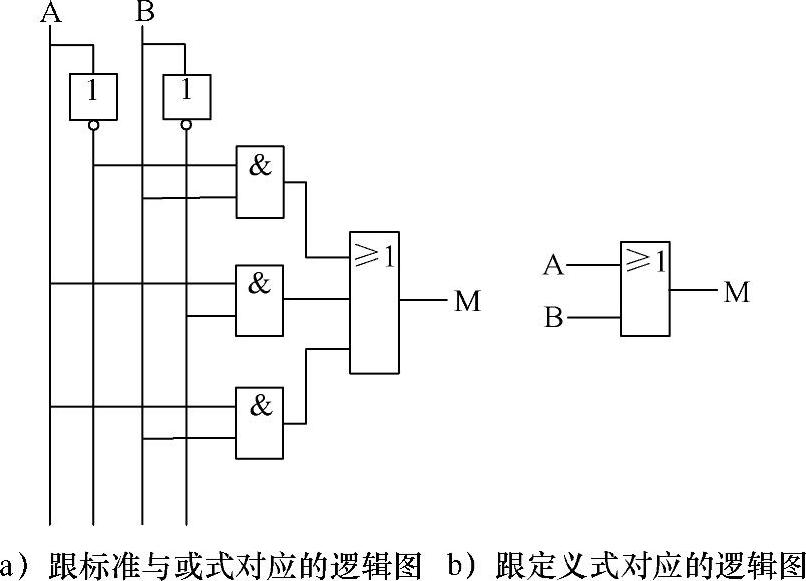
图4-13 或逻辑的两种表达式对应的逻辑图

逻辑代数把“只有1个变量互补、其他因子相同的两个乘积项”称为逻辑相邻项（简称为相邻项）。

一对相邻项相或，利用

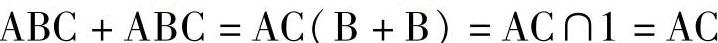
的原理，消去其中的互补变量，合并为一个新的乘积项，达到减少乘积项个数和乘积项中变量个数的化简效果。

通过反复结组合并、不断消除变量、减少乘积项，直到乘积项都不相邻、无变量可消时，表达式就可能被化到最简了。

（2）公式法

完全用表达式实现化简叫做公式法化简。

【例4-5】对或运算的标准与或式进行化简：

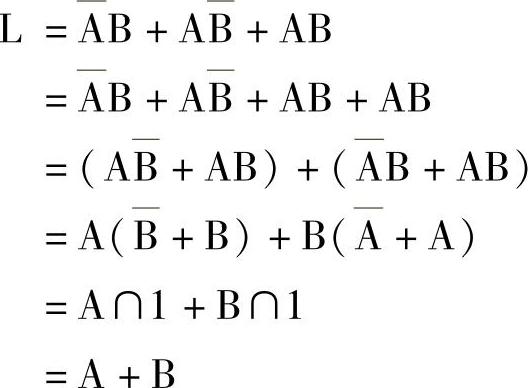
用公式法对一般结构的与或式化简时，需要将其变换为标准与或式，再结组化简，如：

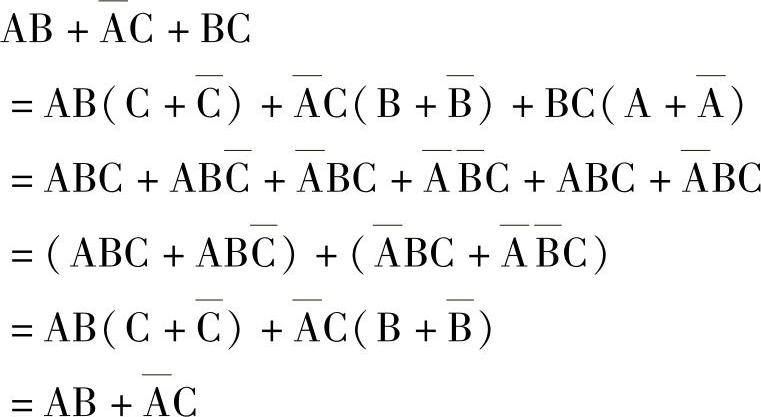
（3）图形法

1）卡诺图：用真值表转换成的化简工具叫卡诺图，卡诺图的本质还是真值表，是变量取值采用特殊排序方式的矩阵形真值表。

卡诺图和真值表一样，跟标准与或表达式有严格的对应关系。卡诺图中的方格，既对应全部变量的各取值组合及函数值，又对应最小项。

图4-14所示分别为二变量卡诺图、三变量卡诺图和四变量卡诺图，它们由表4-13、表4-14、表4-15所示真值表变换结构方式而成。

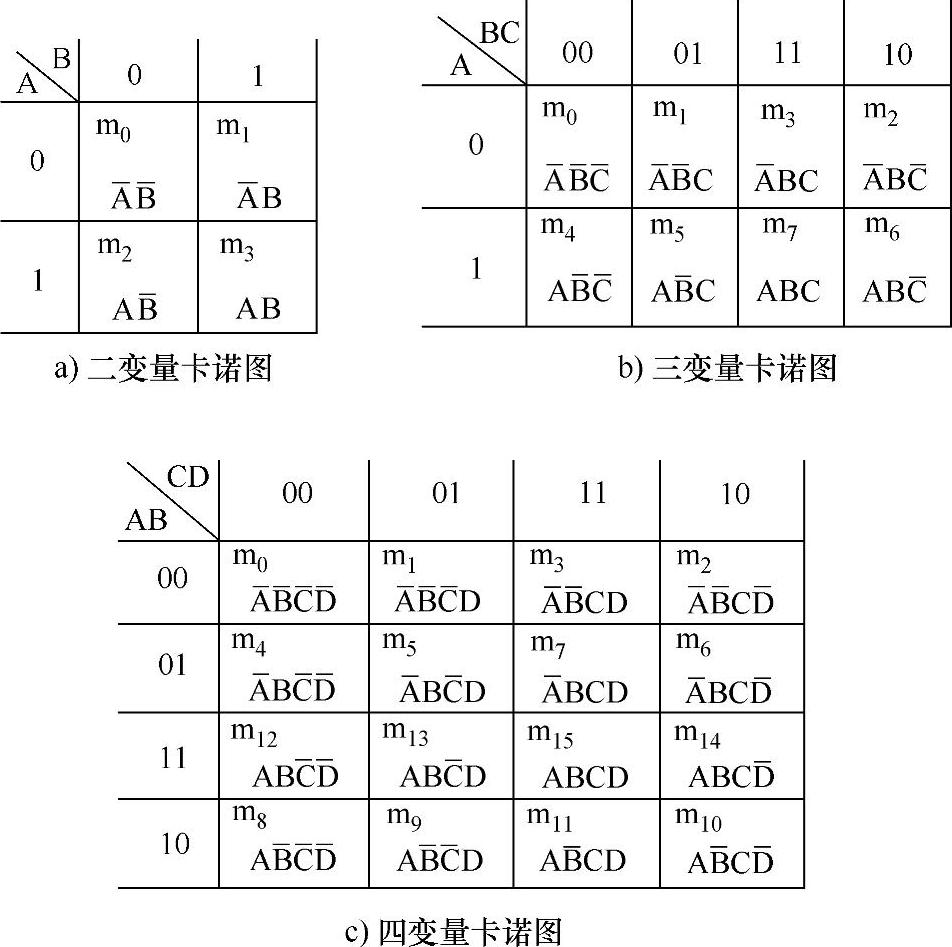
图4-14 二、三、四变量卡诺图

制作一个逻辑函数的卡诺图，可依据函数的标准与或式直接填制。为使卡诺图内容简洁，习惯上只填一种函数值。【例4-6】制作函数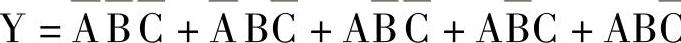的卡诺图。

这个函数表达式已经是标准与或式，可按其中包含的最小项直接填制卡诺图。具体步骤如下：

第1步，画出三变量空白卡诺图。

第2步，按表达式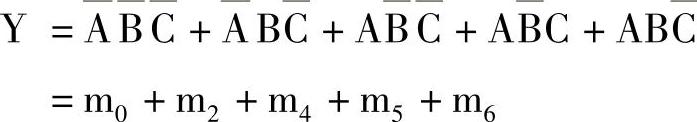

在卡诺图的相应空格中填写1，得到的卡诺图如图4-15所示。

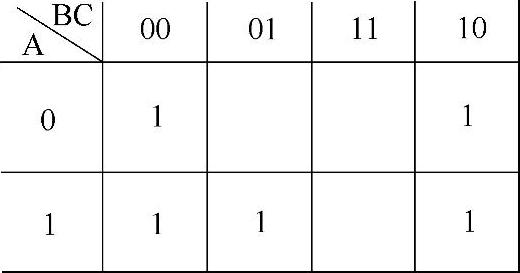
图4-15 例4-6的卡诺图

卡诺图跟真值表一样，是与函数的标准与或表达式相对应的，制作卡诺图之前通常将函数表达式转换为标准与或式，再填制卡诺图。

【例4-7】制作函数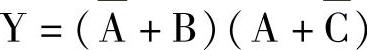的卡诺图

第1步，先将函数表达式转换为标准与或式：

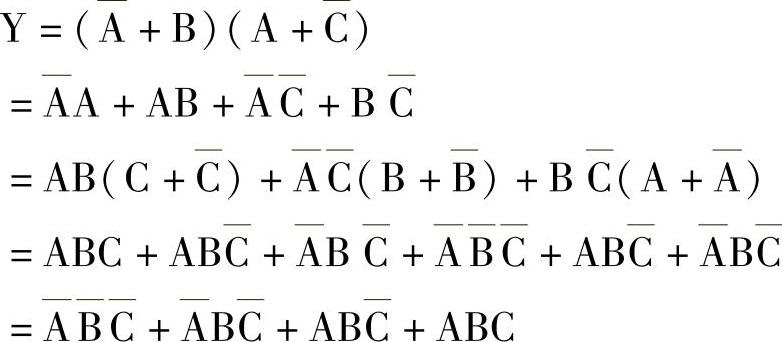
第2步，画出三变量空白卡诺图，然后在4个最小项所在的方格中填入1，如图4-16所示。

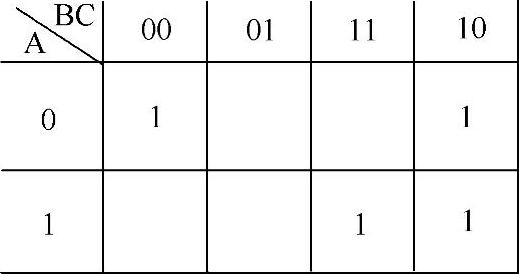
图4-16 例4-7的卡诺图

由一般与或式直接填制卡诺图，称为倒化简法。

【例4-8】制作函数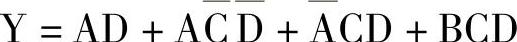的卡诺图。

先按表达式中变量个数画出四变量空白卡诺图，再在图中找出含有表达式中各乘积项为因子的最小项对应的方格，并填入1，如图4-17所示。

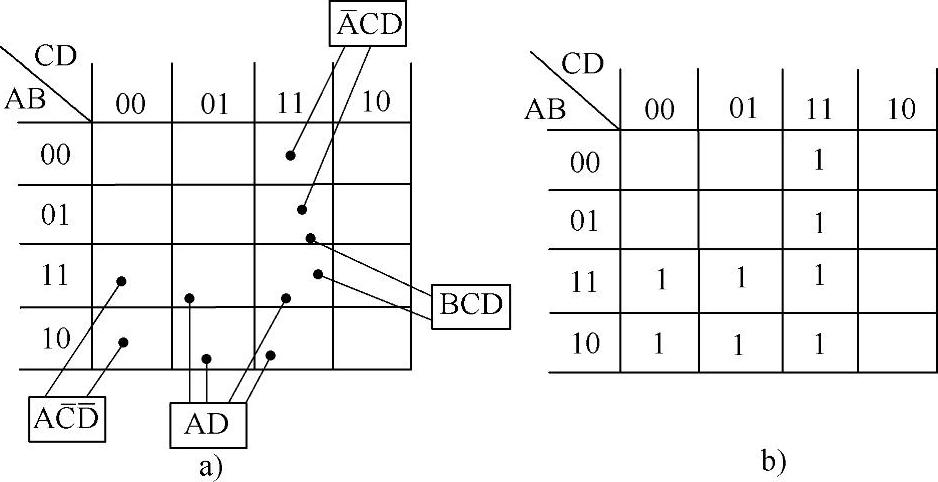
图4-17 例4-8的卡诺图(www.daowen.com)

2）图形法化简：利用卡诺图化简叫图形法化简。

卡诺图的特殊结构使最小项之间逻辑相邻关系转化为位置相邻，把最小项之间的可合并化简关系直观化，并使化简操作简单化。

用公式法化简，需要反复结组合并，如：

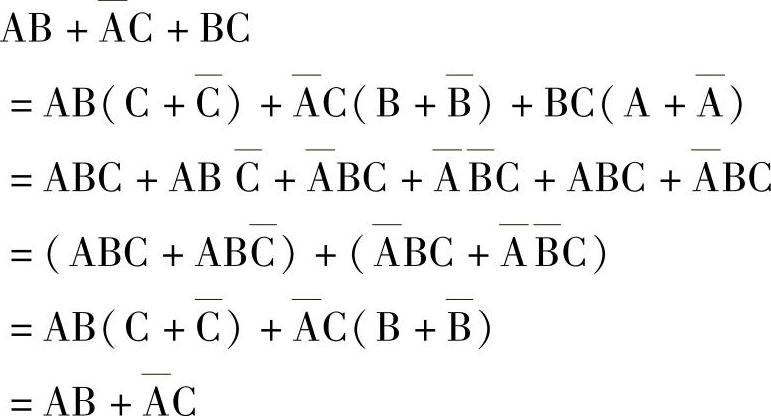
若用图形化简，只是在卡诺图上画两个圈（称为圈项），就能得到函数化简后的最简与或表达式，既直观又简单，如图4-18所示。

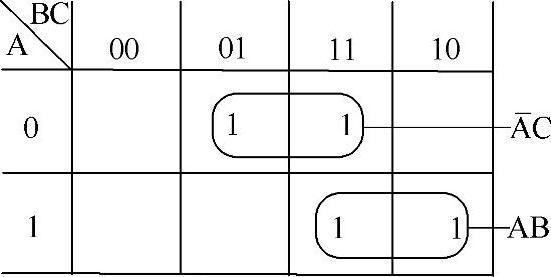
图4-18 AB+AC+BC的卡诺图化简

3）圈项规则：用卡诺图圈项化简，被圈的必须是相邻的同值方格（所以卡诺图中只填一种值），方格数为2的整数幂。

2¹（2）个相邻最小项相或，可消去其中的互反变量，合并为一个乘积项，如图4-19所示。

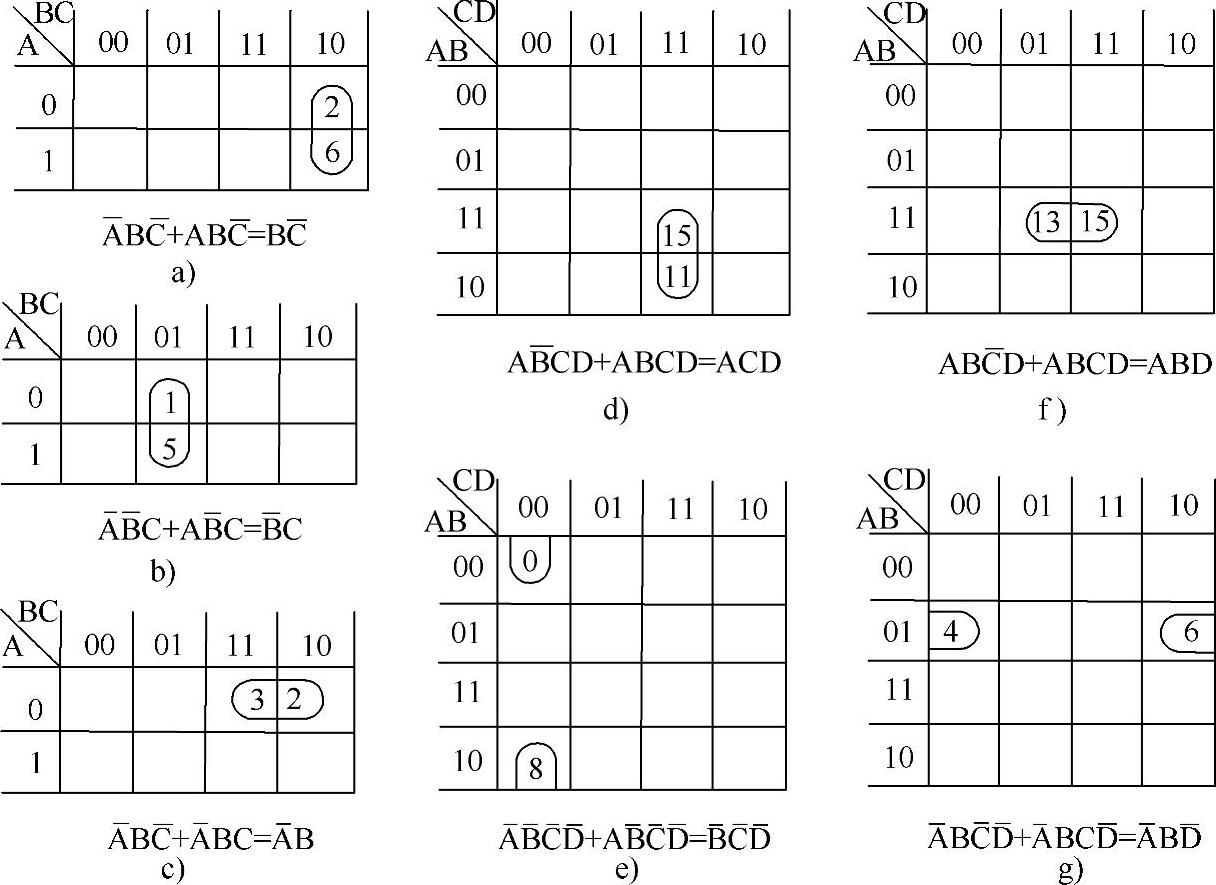
图4-19 两个相邻项合并的类型

2²（4）个相邻最小项相或，可消去其中的互反变量，合并为一个乘积项，如图4-20所示。

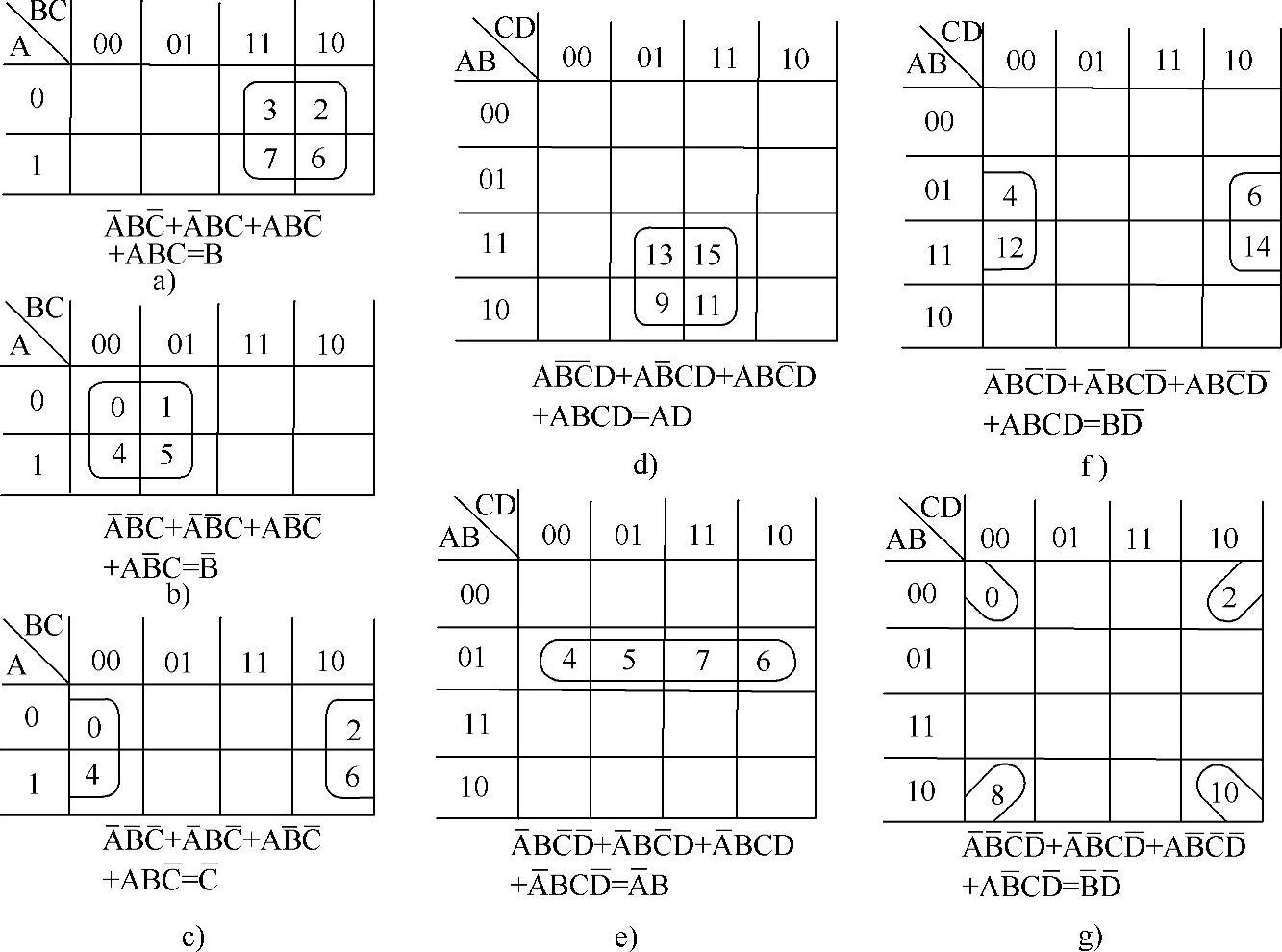
图4-20 4个相邻项合并的类型

2³（8）个相邻最小项相或，可消去其中的3个互反变量，合并为一个乘积项，如图4_-21所示。

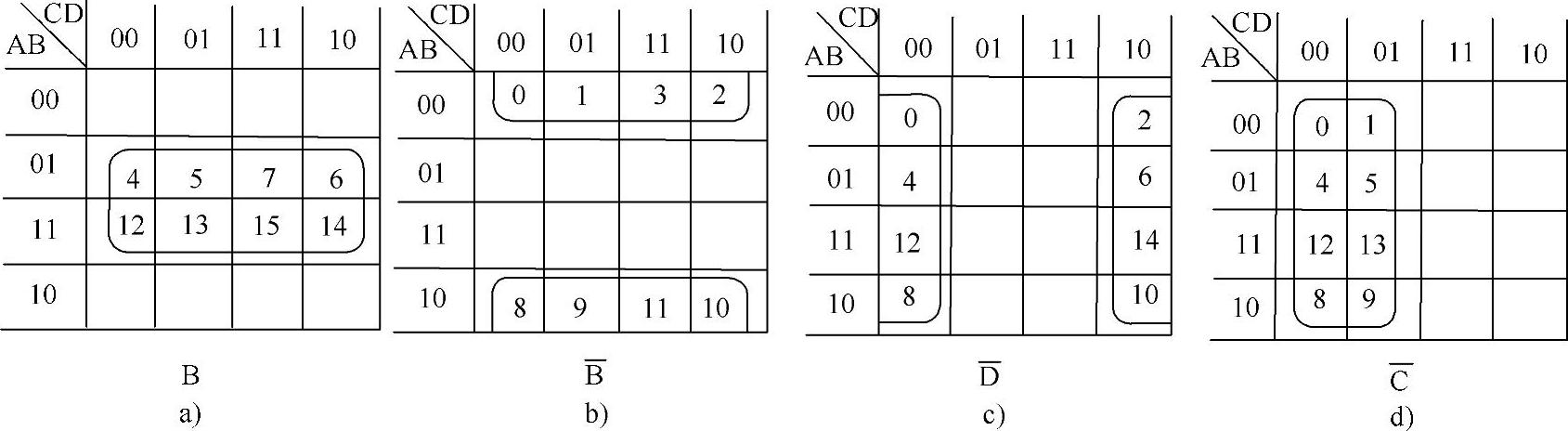
图4-21 8个相邻项合并的类型

4）用卡诺图化简表达式的步骤：

①将表达式变换为标准与或式，做出逻辑函数的卡诺图；

②确定最小项之间的相邻结组关系，在图中画出圈项线，并写出每个圈项的合并结果；

③将各圈项得到的新乘积项相加，写出化简后的与或表达式。

最小项的相邻项数量等于变量个数。在化简时，一个最小项可参与多组合并，或运算的重叠律A=A+A说明一项多用是合法的。

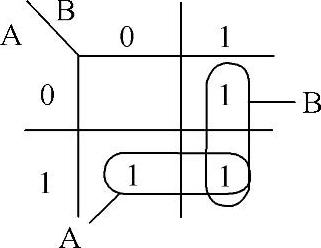
图4-22 或运算标准与或式的化简

或运算的重叠律在图形法化简中表现为一个最小项可参与多个圈项合并的化简方法，目的在于使化简一次达到最简。上式的图形化简如图4-22所示。

图形化简的圈项合并时要遵循“能大不小”的原则，充分利用或运算的重叠律，使圈项范围达到最大，可确保化简能一次达到最简的结果。【例4-9】用卡诺图化简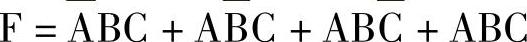，如图4-23所示。

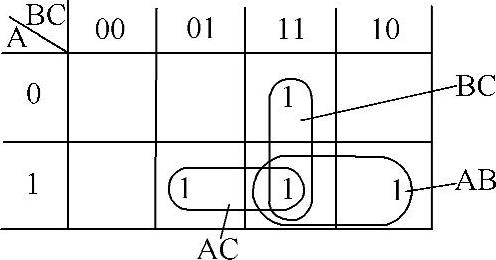
图4-23 例4-9的卡诺图

化简结果：F=AB+BC+AC“能大不小”的规则不是绝对的，要因题而异。

【例4-10】化简特例，如图4-24所示。

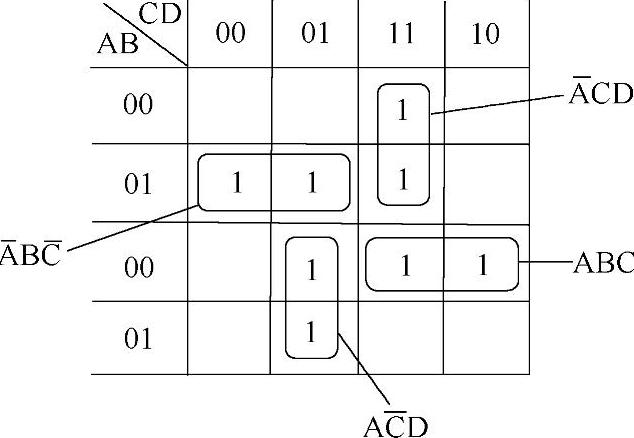
图4-24 不能大范围圈项的特例

对于具有约束项或无关项的函数，有约束项的再用ϕ或×标出约束项的位置，可借助约束项（或无关项）把表达式化简得更简单。【例4-11】利用约束项化简，函数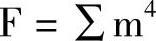（2，3，4，5，6，7，11，14）的约束项条件是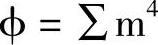：（9，10，13，15）。

化简如图4-25所示。

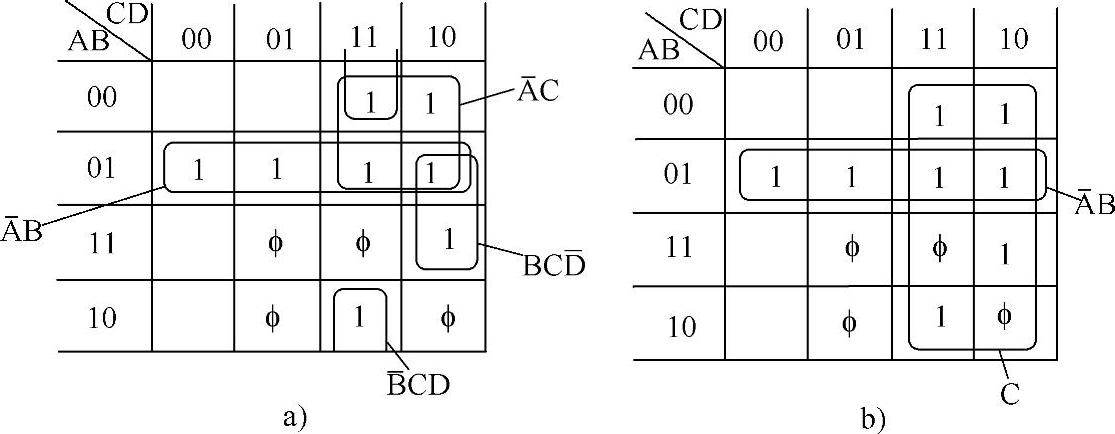
图4-25 例4-11的卡诺图

图4-25a所示为不考虑约束条件的化简结果：AC+AB+BC D+BCD。

图4-25b所示为利用约束条件的化简结果：。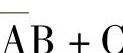

图4-26所示为三例未达最简的化简圈项以及正确圈项方法对照。

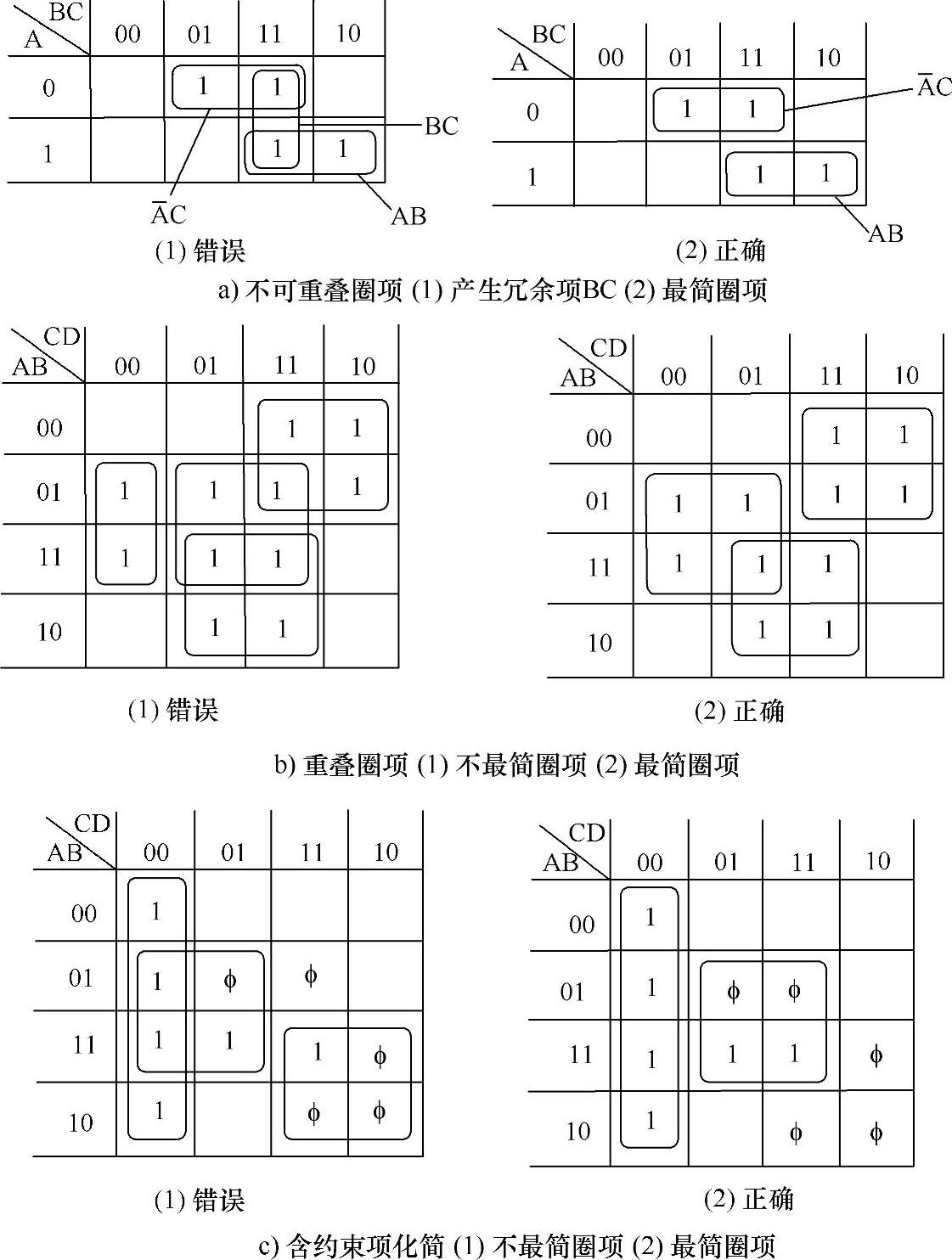
图4-26 不最简的圈项及对照

在可以化简的逻辑函数中，有一部分函数的最简结果不是唯一的，如图4-27所示。

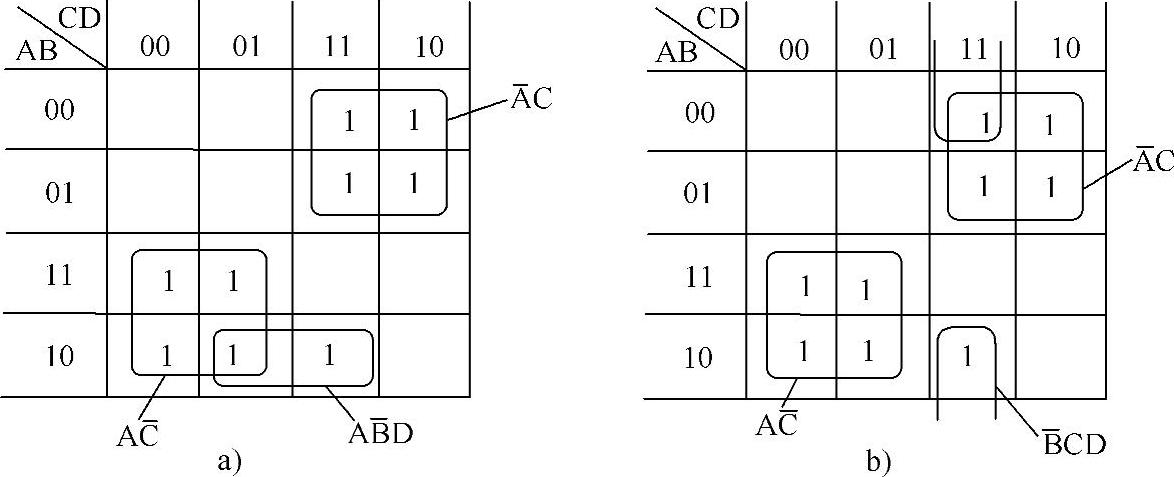
图4-27 最简结果不唯一的化简实例

利用反函数化简也是图形法化简的常用手段。

【例4-12】用卡诺图推证摩根定理。设F=AB，则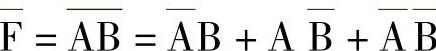。用卡诺图对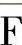化简，如图4-28所示。所以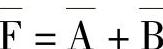，即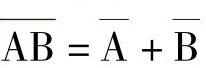

卡诺图化简法常用在不多于5个变量的逻辑函数的化简（本书未用五变量卡诺图）。在数字电路的实际制作中，电路的主体结构通常选用集成电路成品，需要制作者设计的只是一些较简单的辅助性电路，用以解决各芯片之间的匹配问题，信号数量少，公式法和图形法的化简手段都适用。

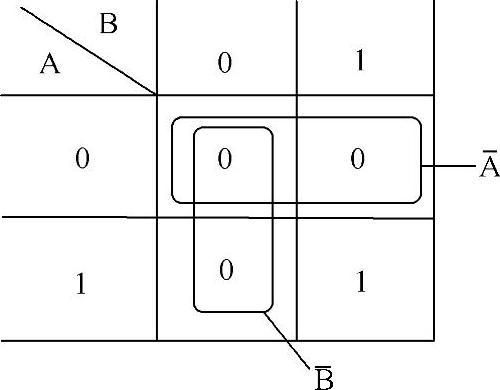
图4-28 利用反函数的化简