1.双环条件与单环条件之间的内在联系

任何一个典型图形都可以列出4个单环条件和3个双环条件。以图形D为例，由表1可以查出它的4个单环条件为:

以及3个双环条件为:

上述每个双环条件都可以表达成2个单环条件的和或差，例如，无1，6双环条件可以表达成(F-1)式中的第1和第2两个单环条件之差，也可以表达成第3和第4两个单环条件之差，即

或

同样地，无2、4和无3、5两个双环条件也都可以表达成某两个单环条件之差或和。无2、4双环条件可以表达为:

或

对于无3、5双环条件，则有

或

在(F-3a)式中，是第1与第2两个单环条件之差，不难看出，其中ε1因为两条件相减而被抵消，因此，不论ε1等于多大，实际上对无1、6双环条件的闭合差不会产生影响，同样，在(F-3b)式中的ε6，也因两条件相减而抵消，因此，(F-3a)和(F-3b)两式又可写成如下形式:

同理，(F-4a)式与(F-4b)式以及(F-5a)式与(F-5b)式也都可以分别写成简化的形式，即

同理，对无2、4双环条件而言，则可写成以下形式:

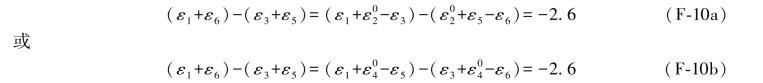
对于无3、5双环条件，则有:

2.综合误差与双环条件的异同及其计算方法

当一个典型图形中的6个原观测值Li通过水准测量取得其成果之后，就可列出单环条件或双环条件，并由此可以算得6个双差和方程，例如，图形D的双差和方程为:

如果能够求出双差和方程的原真误差εi或综合误差(i)(i＝1，2，…，6)，那么它的真值也就解决了。

上述各双差和方程中的综合误差(i)的表达式在表6.7中已经给出，即

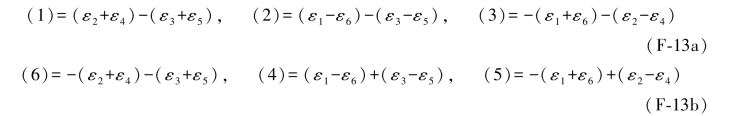
以上的综合误差(1)和(6)的公式可以改写成如下形式，即

而在(F-6a)和(F-6b)两式中给出了无1、6双环条件的两种表达形式，前一个是(ε2-ε4)-(ε3-ε5)＝(ε2-ε3)-(ε4-ε5)＝-10.2，将此式与(F-14a)式中的综合误差(1)相比较即可看出，其中(ε2-ε3)项相等，只有(ε4-ε5)项的前置符号相反，同样，后一个是(ε2-ε4)-(ε3-ε5)＝(ε2+ε5)-(ε3+ε4)＝-10.2，其中(ε2+ε5)项前置符号相反，但(ε3+ε4)项前置符号则相同。类似地，如果将综合误差(2)与(4)的公式以及(3)与(5)的公式也作相应的改变，则有

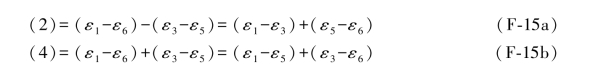
以及

附表1　图形D双环条件与综合误差公式对照表

续表

由(F-17a)式列出的4个单环条件以及3个双环条件分别为:

将以上各式与表1.1中所给出的由原观测值列出的相应条件相比较知，其中第1、2单环条件的闭合差由-4.1和6.1改变成-5.3和4.9，而第3、4单环条件的闭合差保持不变。从3个双环条件来看，其中第1、2两个双环条件闭合差分别由-2.6、4.6改变成-3.8、3.4。而第3双环条件，也就是无1、6双环条件，其闭合差保持不变，仍等于-10.2。从附表1可以看出，无1、6双环条件可以写成如下形式:

而综合误差则为:

由附表1.1知，无1、6双环条件以及综合误差(6)分别为:

3.应用两个特殊值以及其他途径识别对边的真值

1)关于特殊值问题:

从上面的讨论可以看出，要求出对边的真值或者要确定对边的综合误差值，关键在于识别搜索值是否正好就是真值，而真值的唯一特征就是真误差应为零。

式中，ε1等于零，ε6等于特殊值58.9372的真误差(ε2+ε4)。如果由(F-21a)式再列出它的4单环条件，则有:

上述4个单环条件的闭合差有着明显的特点，即第3个与第4个闭合差数值均为5.3，但正负相反，第2与第3个闭合差也是数值相等正负相反，这是由特殊值列出单环条件时所具有的另一个特点。

若将(F-21c)式中的误差距数值代入(F-22c)式的误差距条件中，则有:

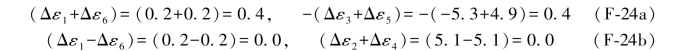
这就验证了上述第三点所讲的结论。

若以另一个特殊值58.9368+(ε3+ε5)替换(F-21a)中的58.9372，则有

按照前面所讲的同样方法，列出两组相应的双环条件，则有

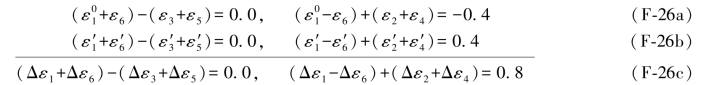
(F-25a)式的真误差向量为:(www.daowen.com)

由(F-25a)式列出4个单环条件应为:

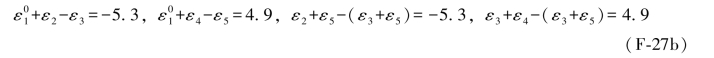
上述4个闭合差仍具有一定的规律，即第1与第3个闭合差数值相等正负同号，而第2与第4个闭合差也是数值相等正负同号。若将(F-25c)式中的误差距数值代入(F-26c)式，则有:

上述结果仍符合前文第三点中所讲的结论。

随着搜索值越来越趋近于真值时，其真误差越来越小，直到ε6或ε1等于零，于是有:

上式中互为对边的双差和方程，其中(2)+(4)＝0.0，(3)+(5)＝0.0，故有:

于是有

上述结果正好与(F-30a)式中双环条件的闭合差相吻合，除此之外，也可以直接应用(7-7c)式中的误差距进行计算。因为在L1与L6均为真值时，再生真误差＝0.0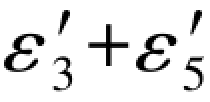，＝0.0，于是可以写出以下结果:

上述结果仍与(F-30a)式中的闭合差相吻合。

因为在搜索过程中，只可能有一次是搜索值正好等于真值的情况，所以只有当探索值正好等于真值时，上述所有计算结果都将彼此相吻合。为了进一步验证解的正确性，还需进行必要的复核，以便从不同角度验证解的正确性。

a.由它列出的4个单环条件(即(F-30d)式)应为:

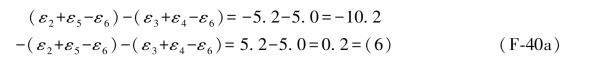
或者是

上述结果与(F-30a)中的双环条件闭合差相吻合。

c.通过等值双环条件的结构说明求真法解题的实质。

任何一个典型图形都可以列出3个双环条件，随着已知边(指高差真值为已知的边)所在位置的不同，为了清晰起见，通常采用3种形式来安排这3个双环条件的先后次序。例如，对于图形D而言，就是表6.4中所给出的3组情况。此外，每个双环条件又可以有两种不同的表达形式，其一就是全部以原真误差表达的双环条件，另一种就是主项为原真误差，而其副项则是用再生真误差的表达形式。例如，在表7.4中的第1、2、3组就分别给出了不同情况下两种表达形式的双环条件。

很明显，两式中的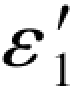都是正负抵消，所以闭合差分别等于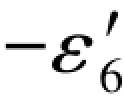和。

对于其他情况，原因相同，下面只是直接写出其结果，不难从公式的本身看出其应有的结果。(7-17a)和(7-18a)两式可以写成为:

从以上讨论可以看出，利用等值关系将双环条件写成等值双环条件，对于理解数值之间的变化关系能够显现出明显的规律。

(F-44a)式是由(F-39b)式列出的两个双环条件，(F-44b)式是两个等值双环条件，上下两式互相对应，闭合差相同。其中画有横线的项是双环条件的副项，它们的数值不随L1或L6的改变而变动，始终是一个确定的常数。如果现在用表1.1中的相应数值代入以上两式，则有

(F-44c)式是将数值代入(F-44a)式后的结果，(F-44d)式则是代入(F-44b)式后的结果，不难看出，由于副项是等值关系，闭合差数值相等。

综合以上的讨论，现在再来分析一下搜索对边真值的原理。

通过以上讨论可以得到两点结论:①对于任一典型图形，由某已知边求其对边真值时，总是有解，而且解是唯一的，既不可能无解，也不可能出现多个解。②实际解算时，难点在于及时判断是否已经找到了对边的真值。为此，必须经过反复检验与复核，以免造成误判。

类似地，在(F-47a)式中，如果将+(ε1-ε6)称为“第1副项”，将-(ε3-ε5)称为“第2副项”，则综合误差(2)和(4)就可以分别表达为:

同样，将(F-51a)式中的-(ε1+ε6)称为“第1副项”，将-(ε2-ε4)称为“第2副项”，则综合误差(3)和(5)即可分别表达为:

前面提及，在搜索某边的真值时，其双环条件与一真再生向量的双环条件唯一不同之处仅仅是在主项中的再生真误差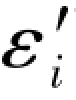改变成搜索值的真误差εi，所有副项都没有任何改变，所以上述各综合误差表达式仍然没有变动，而且所有副项的数值都是固定的常数，例如，由(F-44c)式和(F-44d)式知:

故由(F-55a)和(F-55b)式得:

由(F-47c)式和(F-47d)式知:

故由(F-56a)和(F-56b)式得:

又由(F-51c)和(F-51d)两式知:

故由(F-57a)和(F-57b)两式得: