球体积公式

球体积公式

两千多年前，发生了这样一个故事。

杠杆原理的发现者——古希腊科学泰斗阿基米德，利用杠杆原理“称”出了球体积公式。

用一根长为球直径2倍的长杆，即为4r的杆，确定一个支点N。将杆的中点支于支点。两端点设为S、T。NT的中点为O。以O为心，以球半径r为半径画圆，并画圆的外切正方形及等腰三角形NBC，使∠CNT＝∠BNT＝45°。这图形绕ST旋转得到球、圆柱和圆锥。

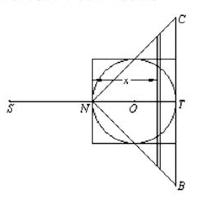
在离支点x处切一铅直狭条，宽度记为Δx。旋转后得到的是厚为Δx的圆盘。这些薄片体积的近似值分别是：

球部分：πx（2r－x）Δx，

圆柱部分：πr2Δx，

圆锥部分：πx2Δx。

阿基米德将从球和圆锥割出的两个薄片吊在端点T，它们的合力矩（重力×重力臂）为

2r[πx(2r－x)Δx＋πx2Δx]＝4πr2xΔx

＝4x·(πr2Δx)

这正好是圆柱部分薄片吊在原处力矩x·πr2Δx的4倍。

把从N到T所有割出的薄片加在一起，将球和圆锥用绳子吊在S点，其力臂是2r，把圆柱的重心吊在O点，它的力臂是r。它们的力矩也应满足4倍关系，即球和圆锥吊在S点与4个圆柱吊在O点杠杆平衡，于是

2r（球体积＋圆锥体积）＝4r（圆柱体积）。

已知：

圆锥体积＝，

圆柱体积＝2πr3，

代入后立得：

球体积＝。由此公式可得球体积是它的外切正圆柱体积的。

多么精彩的方法。竟然用秤称出了球的体积公式。当然阿基米德在称得球体积公式以后，仍然用数学方法严密地证明了他的发现。阿基米德的方法启示我们，数学定理与公式蕴藏在现实世界之中，它们往往与物理、化学、生物学……的规律联系在一起，我们可以通过物理的、化学的、生物的方法去发现它们。

我国古代数学家对球体积公式也有研究。

西汉末年成书的«九章算术»中，已经记载着柱、锥、台、球等各种体积的计算问题。除了球以外，其他各体积公式都和现在一致。由于球的体积比较难求，当时未能找到正确公式。书中所载的球体积算法，相当于V≈，它的误差太大了。

«九章算术»成书后，人们逐渐发现了这一问题，在科学家张衡的脑子里出现了一个有价值的思想。他设想了一个边长等于球直径的立方体，把球装在里面，使它们相切。他想：若能求出立方体与内切球的体积之比，球体积问题便容易解决了。这种想法是数学中比较“标准”的想法——把比较难解决的问题转化为可以解决或相对容易解决的问题。遗憾的是，他的计算方法不够科学，最后推出立方体与球的体积之比为8∶5，这比原来的误差更大。结果虽然不够理想，但张衡的研究方法却给了后人有益的启示。

到了三国时代，大数学家刘徽发现了一条重要原理：如果对于两个等高的立体，用平行于底面的平面截得的面积之比是一常数，则这两立体的体积之比也等于该常数。这一原理可称为“刘徽原理”。在用“刘徽原理”证明了圆锥、圆台等旋转体的体积公式后，刘徽便集中精力解决球体积问题。他发现了«九章算术»和张衡研究中的错误，也从张衡的研究方法中得到启示，他试图通过刘徽原理把球体积转化为另一个能求出体积的立体——“牟合方盖”中去，以便求出正确的球体积公式。虽经认真研究，但最终他还是没能找到“牟合方盖”的体积与球体积之间的关系，从而未能正确求出球体积，只能暂时搁下“以俟能言者”。

二百年以后，有一位“能言者”站了出来，这人就是祖冲之的儿子。他沿着刘徽开辟的道路继续前进，适当改进了研究方法，终于完成了刘徽的未竟之业，彻底解决了球体积问题。