答 案
第2关 空缺的数
21。
观察前五个数字可知,其变化规律是加2、加3、加4、加5,最后两个数字之间是加8,由此可知空缺的数字与前后两个数字之间的规律是加6和加7。因此,问号代表的数字为21。
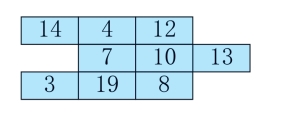
第3关 方框内填数
第4关 分割圆
5。
每个圆中左右两个数字之和再加3等于下面的数字。
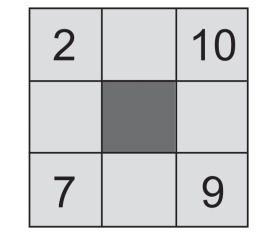
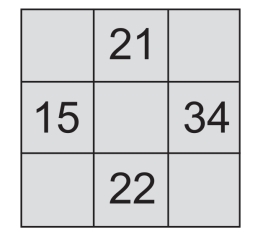
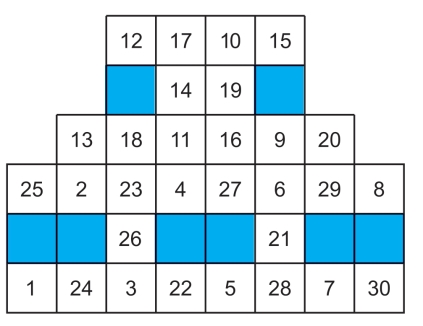
第5关 方格填数

第6关 符号代数
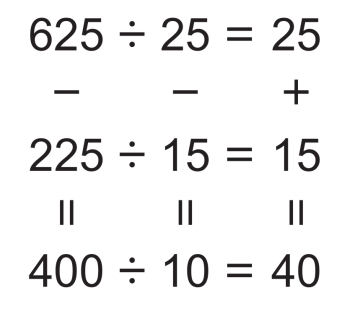
第7关 完成谜题
10。
每个方块下面数字积与上面数字积的差,用中心的罗马数字来表示。
比如:7×6-6×3=24。
第8关 数字格子
每个数字按顺时针旋转,该数字即为其要旋转的次数。
第9关 运动中的数字
每个数字按顺时针方向旋转,旋转的次数为该数字减去1。
第10关 数字和字母的关系
K。
每行中间数字等于左侧字母的正序值加上右侧字母的倒序值。
比如:I的正序值是9,E的倒序值是22,
9+22=31。
第11关 “数字·字母”转盘
B。
根据26个英文字母的位次顺序,图中每个字母的位次数是其对面扇形中数字的2/3。
比如:F的位次是6,即9×2/3=6。
第12关 “数字·字母”正方形
10。
根据字母在英文字母表中的位次数。从E开始,按顺时针方向,加1,加2,加3,加4,加5,然后再加1,依此类推。
第13关 填什么数字
27。
从左端下面A开始,图中字母按字母表顺序出现,但每次省略两个字母,图中数字代表省略的两个字母位置号之和。当到达字母表末尾时,再次从头开始。
即问号处是26(Z)+1(A)=27。
第14关 填什么字母
GC—73。
中间框中的两位数中,十位上的数字表示前后两个框中的前一个字母在字母表正序和倒序的位置号,个位上的数字表示前后两框中后一个字母在字母表正序和倒序的位置号。
比如:H的正序号是8,S的倒序号也是8。
第15关 缺失的字母
S。
根据26个英文字母的位次数,用上面的字母值与右面的字母值之和,减去左面的字母值与下面的字母值之和,得数即为中间的数字或者中间字母的数值。
比如:5(E)+9(I)-3(C)-4(D)=7。
第16关 藏宝箱
D是49,E是44。
每个单词后面的数值都等于该单词第一个、中间和最后一个字母在字母表中序号之和,所以
S+K+S=19+11+19=49,Y+E+N=25+5+14=44。
第17关 排棋子
原来的棋子可以不动,将这五颗棋子重叠放置在原来的布局中就可以了。

第18关 箭靶
两支箭射中了25环,两支箭射中了20环,两支箭射中了3环。
第19关 数字模式
7。
第三行的每个数都是前两行同列数的乘积,第四行的每个数都是同列第二行与第三行数字的和。
比如:(-3)×4=-12,21+(-3)=18。
第20关 丢失的数字
当数字水平地从左往右时,就翻了倍,当数字沿对角线从上往下时,就加2。
第21关 袋子里的棋子
不能做到。
15个袋子放入不同数量的棋子,每袋至少要放入和它本身编号相同数量的棋子,总共是:1+2+3+…+15=120。所以,100个棋子是不够装的。
第22关 填数游戏
A。
A=1,B=2,C=3,D=4,E=5,F=6。
第23关 数字卡片
55。
个位上出现四个数字的概率相等,因此,个位的平均值是(2+3+6+9)/4=5,十位上出现四个数字的概率也相等,十位平均值就是50。所以,平均值是55。
第24关 猜年龄
17岁、28岁、39岁、43岁。
假设A和B的年龄没有相加过,必有(A+C)+(B+D)=(A+D)+(B+C)。根据题意,45+82=56+71=127,则剩下的60为(C+D)。
那么,A+B=127-(C+D)=127-60=67。
由此可知,A和B一个奇数、一个偶数;C和D同为奇数或同为偶数。也就是说,A、B、C、D四个数中有三个数同为奇数或者同为偶数。
假设A、C、D同为奇数或偶数,那么A+C和A+D的值是偶数,即A+C=56,A+D=82或A+C=82,A+D=56,同时C+D=60,A+B=67。最后求得四人的年龄分别是17岁、28岁、39岁、43岁。
第25关 分笔
不合理。
点数和是2、3、4、5的次数和是10次。点数和是6、7的次数和是11次。点数和是其他数的次数和是15次。红色笔应该给掷骰子数和是2、3、4、5的人。
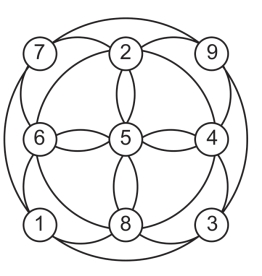
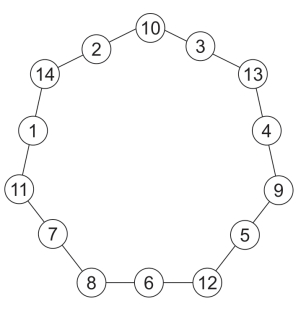
第26关 奇妙圆阵
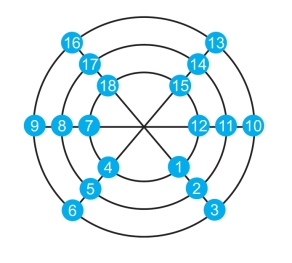
第27关 排数字
答案不唯一。
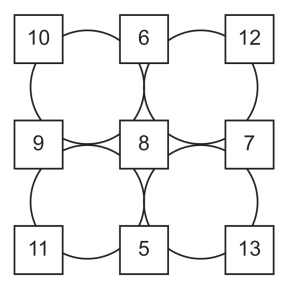
第28关 物品数量
至少八位女士。
不背黑色包的人数=100-82=18(人)
不穿蓝色鞋的人数=100-65=35(人)
不带伞的人数=100-68=32(人)
不戴戒指的人数=100-93=7(人)
所以,至少有100-(18+35+32+7)=8(人)同时拥有这四样物品。
第29关 见面时间
7月19日。
下一次去的天数应该是4、5、7的最小公倍数,即为140,也就是140天后他们三人在培训班再次见面。3月、5月是31天,4月、6月是30天。31×2+30×2=122,140-122=18。3月1日也不能算在内,所以是7月19日他们三人在培训班再次见面。
第30关 圆形下方的数
4。
观察后发现,规律是四周数字的总和乘以2等于中间数字。
比如:(12+4+5+6)×2=54。
第31关 怎么加都是33
第32关 数学天才的难题
第33关 补充数字
12。
观察后发现规律是,图中左侧的1+2+3与4+6+8+3相差15。
第34关 填入数字
3。
观察发现规律是,数字是几就代表它是由几个图形重叠而成的。
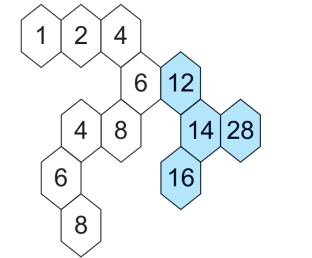
第35关 问号处的数字
4。
每组六边形中,下面的数都等于上面数的平方分别减去1、2、3、4、5。
比如:42-1=15,92-2=79。
第36关 巧妙填数
第37关 分开

第38关 移动棋子
移动四颗。
第39关 图形上的数字
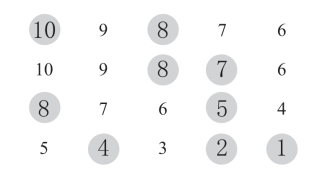
第一横排的数字都是按照从大到小的顺序依次排列的。
第40关 兔子和鸡
兔子有3只,鸡有5只。
可用抬脚的方式解。当让这八只动物抬起一只脚时,落在地上的有22—8=14(只)脚。当让这八只动物再抬起一只脚时,落在地上的有14—8=6(只)脚。每只兔子有四只脚,每只鸡有两只脚。抬过两次脚后,落在地上的脚都是兔子的,所以兔子数为6÷2=3(只)。鸡的数量为8—3=5(只)。
第41关 挂钟
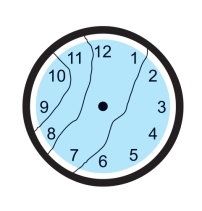
第42关 数字游戏
第二个图答案不唯一。
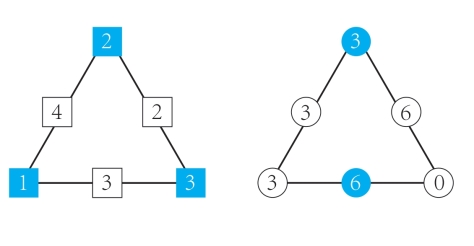
第43关 填数
6。
横向和纵向数字之和都是15。
第44关 第四个正方形
42。
对角数字的乘积都是中间那个数字。
第45关 数字填空
30。
前两个数字相乘,再加上第三个数字,就等于第四个数字。
第46关 正确的数字
17920。
每个数字都等于它下面两个数字的积。
比如5×2=10,8×28=224,80×224=17920。
第47关 问号代表的数
12。
五角星上面一个数字加下面两个数字等于中间两个数字之和。
第48关 填数字
56。
由前三组数可以得出规律:(上边的数字+左边的数字)×右边的数字=中间的数字。所以问号处应填的数字是:(3+11)×4=56。
第49关 巧填等式
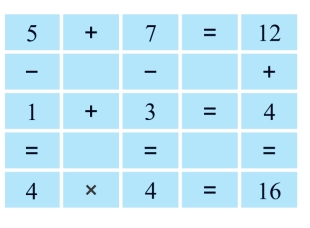
第50关 填一填
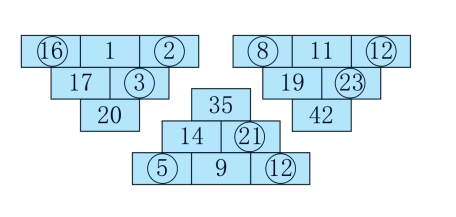
第51关 在三角形中填入数字
23。
5与3的差为2,8与5的差为3,12与8的差为4……因此,推断最后的数字是23,它与17的差是6。
第52关 表格的奥秘
A=17,B=18。
每一行每一列里的数字相加,总和都等于50。
第53关 补充数字
6。
最后一行数字分别是上两行数字之和的平均数。
第54关 计算数字
7。
这是一道找规律的数学题。通过观察本题可以看出,前三行都是一道算式,即第一个数字加上第二个数字然后乘以第三个数字,再减去第四个数字,得出第五个数字。于是有(2+2)×2-1=7,那么,问号处显然是7。
第55关 填入数字
48。
第一行前两个数字的积是第二行第二个数字,后两个数字的积是第二行第四个数字。同理,第三行前两个数字的积是第四行第二个数字,后两个数字的积是第四行第四个数字。由此得出问号处的数字等于4×12,即
48。
第56关 填空
3。
从左上角依次进行运算。
第57关 巧填数字
16。
从题中看,其变化规律依次是:加2、减1,加4、减2,加8、减4,加16、减8。由此知道24后面的数字应该是16。
第58关 排列规律
A:500,1000。
变化规律是交替乘以5和乘以2。
B:203。
规律是各数字依次乘以3再减去1,或者也可以看作是+5,+15(5×3),+45(15×3),+135(45×3)。
第59关 巧填数字
10。
先求出每条斜线上的三个数字之和,上左下右之和减去上右下左之和结果是2,由此得出问号处为10。
第60关 补充完整
72。
图1中18÷2=9,将9分解为3×3,6分解为2×3,图2中84÷7=12,12分解为3×4,8分解为2×4。由此,图3中12分解为2×6。因此问号处的数字为3×6×4=72。
第61关 在正方形角上填数字
9或8。
正方形每一条边上的大数减小数的差分别为2、3、4、5。
第62关 填入图形
问号处应填●。
规律是,(左×右-上)×圆圈深色部分对应的分数=下。
如,(4×9-8)×1/2=14
(3×8-4)×1/2=10
(8×5-16)×3/4=18
则,(9×3-11)×?=16
?=1,即问号处填●。
第63关 填数字
5。
将已知的三个方框中的数字列算式:(5+7+6)÷2=9;(3+14+10)÷3=9;(9+11+16)÷4=9,由此算出,问号处为5。
第64关 问号是几
能,问号处为32。
仔细观察就会发现,对角的两个数字的个位和十位是相互颠倒的。
第65关 问号代表的数字
能,问号处为39。
√=6,★=9,×=3,○=24。
第66关 找规律填数字
能,问号处为65。
先将每个方框上对角数字相乘,再将结果相加,就是前一个方框内的数字。
?=5×9+2×10=65
第67关 数字游戏
能。
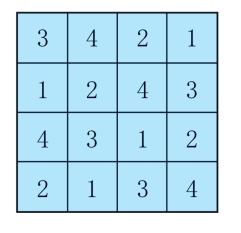
第68关 考考你
4。
将第一条斜线上的三个数字每个都加5,得到的结果为与它平行的第二条斜线上对应的数字,再将第二条斜线上的数字每个都减4,即得出与前两条斜线平行的第三条斜线上的数字。
第69关 找数字
能,这个数字是91。
除91外,其他数字只能被1和它本身整除。
第70关 恰当的数
C。
按顺时针方向看,数字等于前一个图形的边数。
第71关 加数学符号
加上一个小数点就可以了。
第72关 问号处填数字
96。
处于同一条斜线上的数字,每个较小的数字和相邻的较大数字之间形成或乘以2、或乘以4、或乘以8的运算关系,由此算出问号代表的数字可能为6144、3072、1536、384、192或96,其中两位数只有96,所以答案是96。
第73关 推算
11。
左边图形左半圆三个数字相加得到13,右半圆三个数字相加等到16。右边图形右半圆3个数字相加得到10,由此可知,问号处的数字为右边图形左半圆三个数字之和,即11。
第74关 错误变正确
把等号上的“-”移动到前面的减号上即可使等式成立,即62=63-1。
第75关 放大镜
都是30°。
无论放大还是缩小,角度不变。
第76关 问号处的数字
1。
这道题每组有四个数字,且第一个数字被第二个和第三个数字连除之后得到第四个数字,即12÷2÷2=3,14÷2÷7=1,18÷3÷2=3,由此可知,问号处应为1。
第77关 划分数字
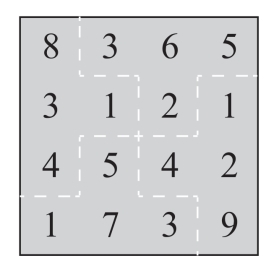
第78关 填入数字
1和9。
B+D=E,E列问号处为9。
E-A=C,C列问号处为1。
第79关 镜子里的数字
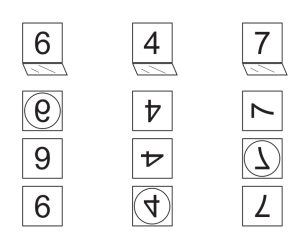
第80关 巧填数字
7。
每行中间的数字等于左边两数字之差加上右边两数字之差。
即,(5-1)+(4-1)=7。
第81关 怎样倒水
先倒300毫升,然后倒掉,再把300毫升杯子装满,将这300毫升水倒进500毫升杯子里,然后再把300毫升杯子倒满,再用这杯水倒满500毫升杯子,此时300毫升杯子里就剩下100毫升水了。
把500毫升杯子里的水倒掉,将水壶中剩下的100毫升水倒进500毫升杯子里,这样两个杯子最后就都剩100毫升水。
第82关 倒霉的兔子
倒霉的兔子是8号。
第83关 一样的年份
1961年。
第84关 未知的数字
能。A是2或0;B是1;C是0。
第85关 赛马
这样的结果是可能出现的。
第一次:甲、乙、丙、丁。
第二次:乙、丙、丁、甲。
第三次:丙、丁、甲、乙。
第四次:丁、甲、乙、丙。
第86关 锯木头
锯五次。
因为90除以15等于6,这根90厘米长的木头,可以分成6段15厘米长的短木头,所以锯五次即可。
第87关 池塘里的睡莲
14天。
睡莲的面积每天增加一倍,那么前一天的面积是今天的1/2,而它第15天可以长满整个池塘水面,因此第14天长满半个池塘。
第88关 小男孩几岁了
7岁。
小男孩年龄的末尾添上一个0就是爷爷的年龄,说明爷爷的年龄是小男孩年龄的10倍。若把小男孩的年龄看成1份,爷爷的年龄就是这样的10份,小男孩的年龄和爷爷的年龄一共11份,也就是77岁,所以,小男孩的年龄是77÷(1+10)=7(岁)
第89关 巧算数字牌
甲取1和9,乙取4和5,丙取3和8,丁取2和6。剩下的牌是7。
丁取的两张牌之商是3,则这两张可能是9、3或3、1或6、2。丙取的两张牌之积是24,则这两张可能是3、8或者4、6。甲取的两张牌之和是10,则这两张可能是1、9或2、8或3、7或4、6。
(1)当丁的两张可能是9、3时,丙不可能是3、8,只能是4、6,则甲只能是2、8,剩余是1、5、7,不存在差是1的数。不成立。
(2)当丁取3、1时,丙取4、6,则甲只能是2、8,则乙无法取到。
(3)当丁取6、2时,丙取3、8,甲拿的两张牌是1、9,乙为4、5,剩下的那张牌是7。
因此,甲拿的两张牌是1、9,乙为4、5,丙为3、8,丁为2、6,剩下的那张牌是7。
第90关 斐波纳奇数列
接下去的数是21。
后面一个数字是前面两个数字之和。
第91关 美丽的郁金香和兰花
只种了一朵兰花。
第92关 套圈
只有套6、19、25这三个数。
第93关 分果汁
把七杯满杯的果汁分别倒一半到七个空杯子中,共21杯半杯的果汁,然后把果汁平均分给三个人。
第94关 比赛的人数
两个人。
参加语文竞赛的有6人,参加数学竞赛的有5人,那么参加竞赛的人数应该是11人,实际上是9人参加,说明有2人参加了语文和数学两项竞赛。
第95关 判断号码
最后一盒子的号码是No.13。
每个盒子的载重数减去其号码都等于11。
第96关 谁在挨饿
不对。如果动物园里的两只熊都是幼熊,它们每只每顿吃10斤肉就够了。
第97关 钟表报时
时针和分针在一条线上时是6点或18点,两针并在一起时是12点或24点,两针成直角时是3点、9点、15点或者21点。
第98关 输了几场
20场。
没有平局,问总只会输多少场,其实就是问要进行多少场比赛。
五个队伍,进行循环赛两次,即进行了20场比赛。
第99关 羊有几只
小明有七只羊,小天有五只羊。
通过小天的话可知,他们两人的羊的数量相差两只。
第100关 奇特的生日
小明的爸爸是闰年2月29日出生的,四年才过一次生日。
小明的爸爸36岁了。
第101关 巧推数字
31131211131221。
每一行数字就是对上一行数字的描述,所以最后一行的数字应该是31131211131221。
比如第二行描述第一行是“一个一”即11,第三行描述第二行是“两个一”即21;第七行描述第六行是“一个三,一个一,两个二,两个一”即13112221。
第102关 汽车
汽车走了110千米。另一个路标上的数字是16061。
已知汽车时速小于等于100千米/小时,所以两小时汽车行驶的距离小于等于100×2=200(千米)。那么,路标的数字小于等于15951+200=16151。在15951~16151符合题意的数字只有16061。
汽车行驶的距离为16061-15951=110(千米)。
第103关 令人迷惑的生卒年
该作家生于1814年,死于1841年。
19世纪,即年份是18开头。另外两个数字和为14-1-8=5。这两个数字的组成可能为0和5,1和4,2和3。这其中只有1和4可以让十位数是个位数的四倍。所以作家生于1814年,死于1841年。
第104关 分酒
将5斤瓶装满后倒至3斤瓶内,再将3斤瓶内的酒倒至8斤瓶里,将5斤瓶剩下2斤倒至3斤瓶。然后5斤瓶再装满酒,之后往3斤瓶内倒,倒满,此时5斤瓶内正好剩4斤酒。把3斤瓶里的3斤酒倒回8斤瓶,此时8斤瓶里也是4斤酒,平分成功。
第105关 存款
丙猜对了,老杨的存款不到100元。
观察四个答案,丙和丁说的话矛盾,所以两人的话一真一假。
假如丙的话为真,甲、乙、丁的话均为假话。
假如丁的话为真,甲的话可能为真,与题目矛盾。
所以,丙的话为真。
第106关 平切表盘
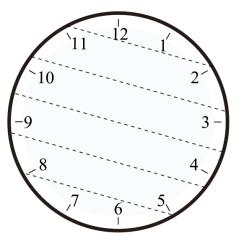
第107关 保险箱

第108关 算术趣题
答案不唯一。
(1+2)-(3+4-5)=1
(1+2+3+4)÷5=2
(1+2+3×4)÷5=3
1×2+3+4-5=4
1+2+3+4-5=5
1×2+3-4+5=6
1×2×3-4+5=7
1+2×3-4+5=8
1+2-3+4+5=9
1+2+3×4-5=10
第109 两位画家
1∶1的比例分发酬劳,因为他们都画了五幅画。
第110关 等式
★=12 ●=4 ◆=6
第111关 图形下方的数
14。
规律是:四周的数字总和乘以2等于中间的数字。
第112关 安徒生童话
第96页和第97页。
两页页码是连续的两个数字。
193÷2=96.5,即一页页码为96,一页页码为97。
第113关 3和100
(1)33×3+33÷33=100
(2)33+33+33+3÷3=100
(3)33×3+333÷333=100
第114关 古怪的等式
观察分析总结规律,得出以下结果。
(1234)×8+(4)=9876
(12345)×8+(5)=98765
(123456)×8+(6)=987654
(1234567)×8+(7)=9876543
(12345678)×8+(8)=98765432
(123456789)×8+(9)=987654321
第115关 喂母鸡
需要喂大约1.97千克米。
因为37千克的米可供37只母鸡吃37天,所以37只母鸡养一天需要喂1千克米。而73只母鸡73天生73千克鸡蛋,所以要得到1千克鸡蛋需将73只鸡养1天,需要喂(1÷37)×73≈1.97(千克)的米。
第116关 四个4等于多少
答案不唯一。
(4×4+4)÷4=5
(4+4÷4)×4=20
4×4+4+4=24
(4+4)×4-4=28
(4×4-4)×4=48
4×4×4+4=68
第117关 买狗
两个人,狗的价钱是100元。
有两个人合买时,狗的价钱是100元;各出5元时,刚好差90元。
第118关 乌龟的年龄
50岁。
设今年乌龟的年龄为x,则五年后的年龄为x+5,由题意列方程:5×(x+5)-5×(x-5)=x,从而得到x=50。
第119关 跳远比赛
小老虎先回到出发点。
小老虎跳完100米刚好跳了50次,全程往返共跳100次。小狮子跳33次,共跳99米,最后1米又要跳1次,往返总共跳了68次。小狮子跳了68次,相当于小老虎跳了102次。因此,当小狮子跳第67次时,小老虎已先回到了出发点。
第120关 数学方法
能,答案不唯一。
例如:9×9+9÷9+9+9=100。
第121关 奇特竖式
应填入8。
五个相同的数加起来个位上得0的话,肯定是偶数,所以能填进圆里的只有2、4、6、8,然后再从这几个里面找出适合条件的就可以了。
第122关 算一算
答案不唯一。
3+2=5
6+4=10
1+7=8
第123关 慢车走了多少千米
132千米。
相遇问题最好画出线段图帮助分析。从9点到12点,快、慢两车同时行驶了3小时,共同走了三个全程:100×3=300(千米)。又因为快车比慢车多走36千米,所以慢车走过的路程为:(100×3-36)÷2=132(千米)。
第124关 图形代表的数字
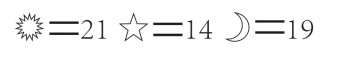
第125关 填等式
21÷3=49÷7=56÷8。
第126关 菱形中的计算
(6+7+11)÷3×2+5-12=9
第127关 巧分苹果
60、16、6、6、6、6。
六个袋子装100个苹果,那么个位数是6的数字是五个,即六个数字中有五个个位数是6,一个个位数是0。
个位数是0的数字为60。那么,其余五个数的和为100-60=40。五个数的个位数都为6,即5×6=30,40-30=10。有一个数字为16,其他四个数字都是6。
第128关 分苹果
84个。
假设大班有小朋友x人,根据题意可得方程:
5x-6=4(x+2)+4
由此算出大班有小朋友18人。则,这筐苹果的个数是:5×18-6=84(个)。
第129关 凑整数
正确选项为D。
通过观察可以看出第一项和第三项个位数相加为10,第二项和第四项个位数相加为10,因此排除B、C选项;已知条件中482大于400,排除A项。所以选D。
第130关 A是多少
A=5。
观察第一个算式,计算后即为A=A。
观察第二个算式,A×A+A=A×6,
即A×(A+1)=A×6,即A+1=6,A=5。
观察第三个算式,(A+A)×A=10×A,
即A+A=10,即A=5。
第131关 快速求和
D。
只算小数点后第二位数即可。
第132关 截木棍
最少要截成五段。
每段的长度分别是1厘米、2厘米、4厘米、8厘米和16厘米。
第133关 猴子搬香蕉
25根。
先背50根到25米处,放下,这时吃了25根,还有25根。
再背剩下的50根,走到25米处时,又吃了25根,还有25根。再拿起地上的25根,一共是50根,继续往家走,再走25米,要吃25根,到家时还剩25根。
第134关 买鸡卖鸡
赚了2元。
第一次9元钱卖掉时赚了1元,第二次11元卖掉时又赚了1元,总共赚了2元。
第135关 吹灭的蜡烛
21岁。
将从1开始以后的连续自然数相加,总和等于231的时候,最后一个数字是21,因此就是21岁。
第136关 三只家禽
一只鸭4千克。
一只鸡+一只鸭=7(千克),一只鸡+一只鸭+一只鹅=12(千克),则一只鹅=5(千克)。
一只鹅+一只鸭=9(千克),则一只鸭是9-5=4(千克)。
第137关 生日是几号
1月2日;答案只有一个。
每两个相邻的星期四之间相差七天。一个月有四个或者五个星期四。假设琳达生日n号,那么,根据条件列示:n+(n+7)+(n+14)+(n+21)=80或
n+(n+7)+(n+14)+(n+21)+(n+28)=80。
解后得n=2,这个月有五个星期四。
第138关 发财
在A国用A国货币换B国货币,再把B国货币带到B国换成A国货币,就是以“保值”的兑换“贬值”的,再把“贬值”的变成“保值”的,周而复始。
第139关 火车的速度
火车的速度是每小时30千米。
不必考虑迈克来回的速度和走多远,就看成他待在最后一节车厢里,10分钟内,火车行驶了5千米即可得出结论。
第140关 年龄
三个女儿的年龄分别为两岁、两岁、九岁。
假设三个女儿的年龄为A、B、C,则,
A+B+C=13
A×B×C=36
推得A、B、C为1、6、6或2、2、9。因为只有一个女儿已经上学,所以应该是2、2、9。
第141关 怎样排队
我们可以排成不规则的形状,也就是说,要想使10个人排成5排,每排4个人,必须1个人当2个人用。
因此,要排成的形状必须内有交点,而且交点必是5个。这样我们就可以很容易想到,符合这样要求的图形是五角星的形状。站成五角星的形状,5个顶点和5个交叉点各站一个,这样就符合老师的要求了。
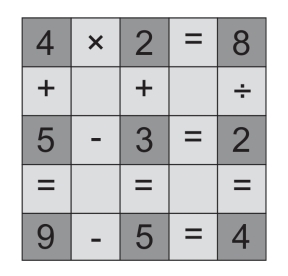
第142关 填数游戏
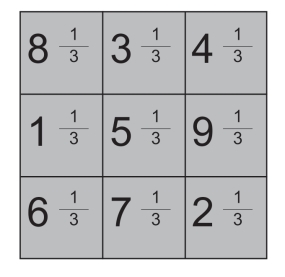
第143关 魔术方阵
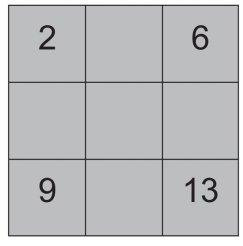
第144关 移动的数字
规律是每个数字顺时针移动次数为本身数字+1次。如数字“1”,顺时针移动(1+1)次。
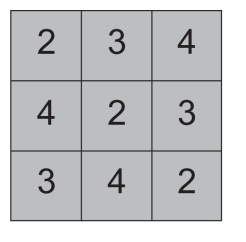
第145关 方格填数
第146关 数字骨牌
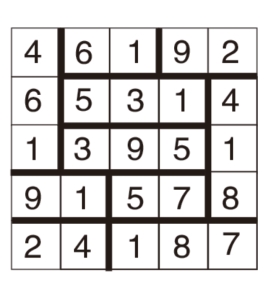
第147关 数字星
7。
每个图形中,第一行差值均为8,第二行商值均为4。
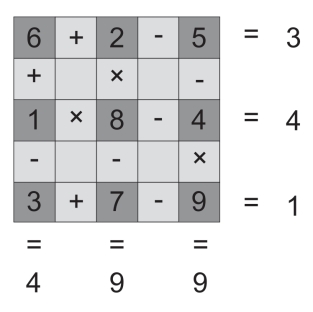
第148关 填充方格
第149关 数字正方形
A=2或18,B=3或12。
A中对角数字之商为3,B中对角数字之商为2。
第150关 数字路口
A=8,B=6。
中间数字是其上、下(或左、右)数字之差。
第151关 填充方格
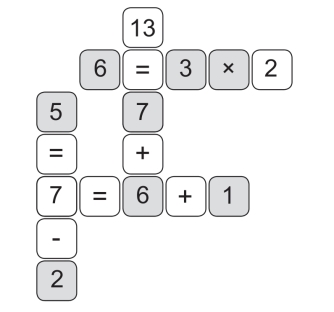
第152关 填充方格
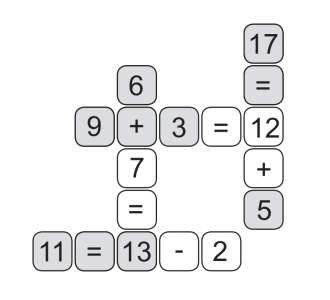
第153关 数字纵横
2。
每一列第一个数字与第三个数字的和的个位数字,等于第二个数字:3+9=12,个位为2;8+6=14,个位为4;7+5=12,个位为2。
第154关 数字六边形
0。
垂线右侧的数的平方减1,是对应的左侧对角处数字。
第155关 数字三角形
A=8,B=4。
图例显示的规律为:(8-2-2)×2=8;(12-2-7)×2=6。
第156关 数字十字架
A=17,B=11。
左、右、上三个数字之和÷下面数字=中间的数字。
第157关 数字方向盘
A=11,B=8。
从最小的一个数开始,按顺时针方向,依次递增2、4、6、8、10。
第158关 数字转盘
A=9,B=2,C=8。
图形A中对角的数字相除等于3,图形B中对角的数字相减等于8,图形C中对角的数字相除等于4。
第159关 数字屋顶
60。
屋顶上的数字=窗户上的数字之和×门上的数字。
第160关 数字圆中方
10。
每个圆内的三个数字(方框外)之和,为同圆内方框内数字的两倍。
第161关 数字地砖
4和9。
每组上面两个数相乘均等于16,下面两个数相除均等于3。
第162关 中心数字
A=24,B=13。
在A组图形中,外边三角形中的三个数相乘,就得到中间三角形中的数字。在B组图形中,小圆圈中的三个数相加,就得到大圆圈的数。
第163关 数字金字塔之巅
16。
从最下面一行看起,底下的两个数的积为上面的数,以此类推。
以最下面一行为例:2×2=4;2×1=2;1×1=1。
第164关 数字金字塔
12。
从最下面一行看起,底下的两个数的和为上面的数,以此类推。
以最下面一行数字为例:4+3=7;3+2=5;2+5=7。
第165关 奇妙幻方
答案不唯一。
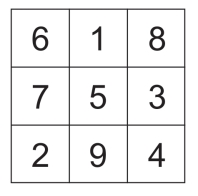
第166关 数字七角星
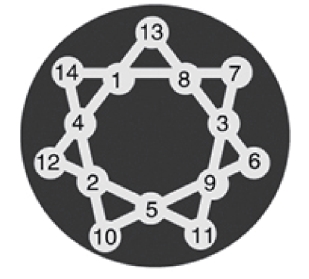
第167关 数字向心力
8。
对角线两侧的数相除,得中间数。
第168关 数码大厦
1。
前两个数之和÷第三个数=第四个数。
第169关 88888888=1000吗
8+8+8+88+888=1000
第170关 填空格
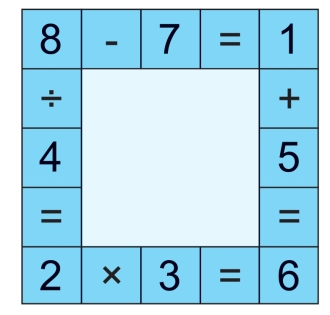
第171关 古树多少岁
579岁。
古柏树说自己的年龄比100大,比1000小,那么可以判断它的年龄一定是一个三位数。又知个、十、百三位的数字之和是21,而且个位上的数字比十位上的数字多2,而十位上的数字要比百位上的数字多2,则个位上的数字就比百位上的数字多4,因此百位上的数字是[21-(2+4)]÷3=5。由此可以得出百位数上的数字为5,那么十位上的数字就是5+2=7,个位上的数字就是7+2=9。由此可以得出,古柏树的年龄为579岁。
第172关 猴子采桃
1534个。
第十天有桃子的个数:1
第九天有桃子的个数:(1+1)×2=4
第八天有桃子的个数:(4+1)×2=10
第七天有桃子的个数:(10+1)×2=22
第六天有桃子的个数:(22+1)×2=46
第五天有桃子的个数:(46+1)×2=94
第四天有桃子的个数:(94+1)×2=190
第三天有桃子的个数:(190+1)×2=382
第二天有桃子的个数:(382+1)×2=766
第一天有桃子的个数:(766+1)×2=1534
即猴子采回来1534个桃子。
第173关 赴宴
10人。
这个问题可以通过列方程式来得到答案。
假设一共有n个人赴宴,那么每个人都要与除了自己之外的人握手。又因为甲乙相互握手的次数是两次,所以总的握手次数是n(n-1)/2。这样一来就能得到一个一元二次方程:n(n-1)/2=45,解开这个方程式,我们能得出答案为10。所以,参加宴会的人数为10人。
第174关 店主亏了多少钱
店主共亏了100元。
他除了收到一张百元假钞外,没有什么别的损失。
如果那张百元钞票是真币,那他并没有赚和亏,如果百元钞票是假钞,就只损失了100元。
第175关 多少钱
小明带了35元,小红没有带钱。书的标价是36元。
假设小明有x元,小红有y元,书的标价为z元(x、y、z均不为负数),那么根据题目条件可以列出如下方程:
x+1=z
y+36=z
x+y<z
解得,x=35,y=0,z=36。
第176关 苍蝇与运动员
300千米。
因为苍蝇每小时飞行速度为100千米,它连续飞行了三个小时没有休息,那么一共飞行了300千米。
第177关 哪个数大
151/301。
如果把各式通分比较分母或分子,算起来就很麻烦。如果把各分数化为小数,算起来也不简单。这就需要你找捷径。通过观察可知道3/7、17/35、101/203都小于1/2,只有151/301大于1/2。
第178关 别致的算式
12345679×(27)=333333333
12345679×(36)=444444444
12345679×(45)=555555555
12345679×(54)=666666666
12345679×(63)=777777777
12345679×(72)=888888888
12345679×(81)=999999999
由于已经知道了12345679×9=111111111;
12345679×18=222222222那么要想知道
12345679×( )=333333333
12345679×( )=444444444
……
很显然就可以知道:
111111111×3=333333333
111111111×4=444444444
111111111×5=555555555
……
所以就知道:
12345679×9×3=333333333
12345679×9×4=444444444
12345679×9×5=555555555
……
所以,正确答案就是9×3;9×4;9×5;9×6;9×7;9×8;9×9,即为27;36;45;54;63;72;81。
第179关 和为1000
四组。分别1000;198、199、200、201、202;55、56、57……68、69、70;28、29、300……50、51、52。
连续数的平均值设为x,1000必须是x的整数倍。
假如连续数的个数为偶数时,那么x就不是整数了。x的2倍只能是5、25、125才行。因为平均值为12.5,要连续80个达不到。125/2=62.5是可以的。
连续数的个数为奇数时,平均值为整数。1000为平均值的奇数倍。1000=2×2×2×5×5×5,x可以为2、4、8、40、200。排除后剩下40和200是可以的。所以答案为平均值为62.5、40、200、1000的四组整数。
第180关 越快越好
9875。
通过观察,可以很容易地知道:
(9871+9879)÷2、(9872+9878)÷2、(9873+9877)÷2、(9874+9876)÷2,都是均等的数字:9875。
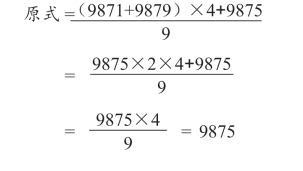
第181关 切割数字蛋糕
25。
较小的数的平方,为对角线另一侧的数。
第182关 数码大厦之门
115。
横行第三个数减第一个数的差的5倍,是第二个数字。
第183关 数字螺旋
A=5,B=7。
中间的数为周围四个数的最小公倍数。
第184关 数字曲径
151,55。
纵向相加结果为999。
第185关 数字密码集
A=7,B=4,C=3,D=4。
每组中每一列的第一个数与第二个数相加再与第三个数相乘结果完全一样。
第186关 数字八卦阵
9。
把外环中的每个数字都看成一个两位数,并把个位数与十位数相乘,再把所得结果加上1,就是对面的内环位置上。
第187关 数字地基
18500。
第一行数字-第二行数字=第三行数字;第二行数字-第三行数字=第四行数字;第三行数字-第四行数字=第五行数字。
35012-16512=18500。
第188关 图形变换
11。
每个格子中各图形全部加起来,即可得到图下所表示的数字。
3▲+4●=10
2▲+5●=9
解得▲=2,●=1。
则5▲+●=11。
