1.滑片的运动及受力分析
(1)滑片的运动
图3.15所示为气缸横截面示意图,图中O点为气缸的中心,O1点为滚动转子的中心,O点至O1点的距离为偏心距e,滚动转子外圆与气缸内圆的切点为T,滑片头部与滚动转子外圆的接触点为A,滑片与气缸内圆的交点为B,∠TOA用θ表示,其中,角度θ为偏心轮轴的旋转角。从图3.15中可以看出,点OO1A组成曲柄连杆机构推动滑片作往复运动,其中,偏心距e为曲柄的长度,滚动转子的半径r为连杆长度。
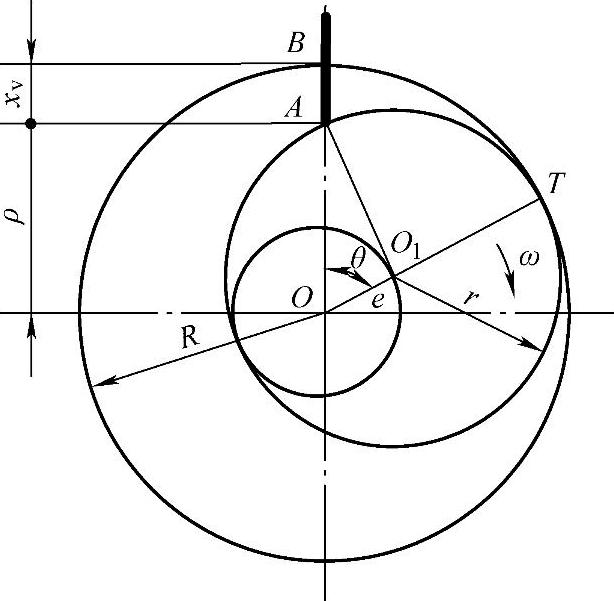
图3.15 滑片的运动规律
假设滑片为刚体,则滑片上任何一点的运动都可以代表滑片的运动,将滑片的位移看成是点A与最高位置点B的距离xv,则当曲柄在任意转角θ、气缸内圆半径为R时,滑片的头部A点的位移为
xv=R-ρ (3.64)
其中,ρ可由图3.15中的几何关系求出

设滚动转子在最高位置B时的转角为0,则有
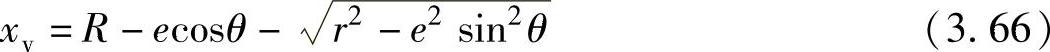
将e/R=ε代入式(3.66),并将式(3.66)的根号项用二项式定理展开,略去展开式中ε二次以上的项,则滑片的位移可以近似表示为
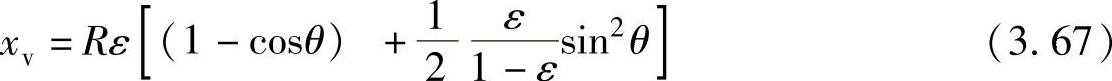
从式(3.67)可以看出,当θ=0或2π时,xv=0,为最小值;当θ=π时,xv=2e,为最大值。
对式(3.67)求导,可分别得到滑片的速度v和加速度av。
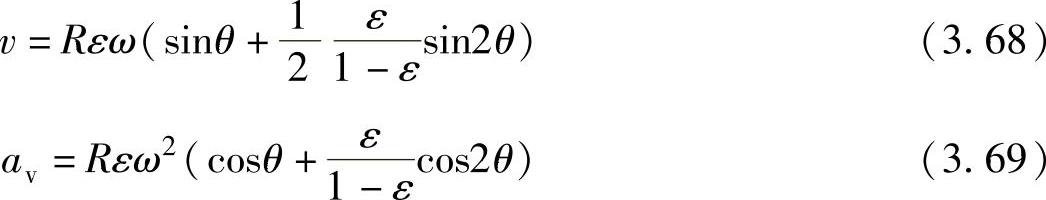
式中 ω——偏心轮轴的角速度,单位为rad/s。
(2)滑片的受力
1)坐标及辅助变量。
图3.16所示为气缸截面的直角坐标及变量。x、y、z轴定于气缸上,原点位于气缸中心点O点上,x轴为滑片的中心线,y轴过气缸中心O与x轴垂直,z轴为偏心轮轴的中心线。主要的变量包括偏心轮轴的旋转角θ及滚动转子的旋转角度φ。连线OOv与连线OvO1的角度α定义为辅助变量。
假设压缩机运转时,滑片头部紧贴着滚动转子外表面作往复运动,则图3.16中α角与其他几何参数之间有以下关系:
(rv+r)sinα=esinθ (3.70)
式中 rv——滑片头部半径,单位为m。
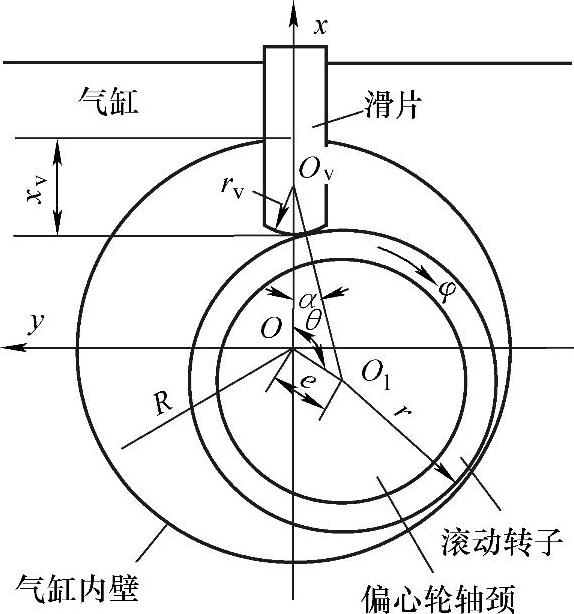
图3.16 坐标与变量
由式(3.70)可得到α与偏心轮轴旋转角θ之间的关系如下:

2)滑片受力分析。
图3.17所示为滑片的受力状况。当滑片在滑片槽内作往复直线运动时,滑片受气缸内外和压缩腔与吸气腔气体压力差、弹簧压力Fs、滑片往复运动惯性力Fi、滑片与滚动转子外表面接触点A的法向力Fn和摩擦力Ft、滑片槽对滑片的支反力和摩擦力的作用。由于滑片两侧的气体压力和油膜状态不同,所以滑片在滑片槽中是倾斜的,有两个接触点G1和G2,从而受到支反力FR1、FR2和摩擦力FRt1、FRt2的作用。另外,滑片在滑片槽中运动时还受到上下端面和两侧面油膜粘滞力和气体力的作用。
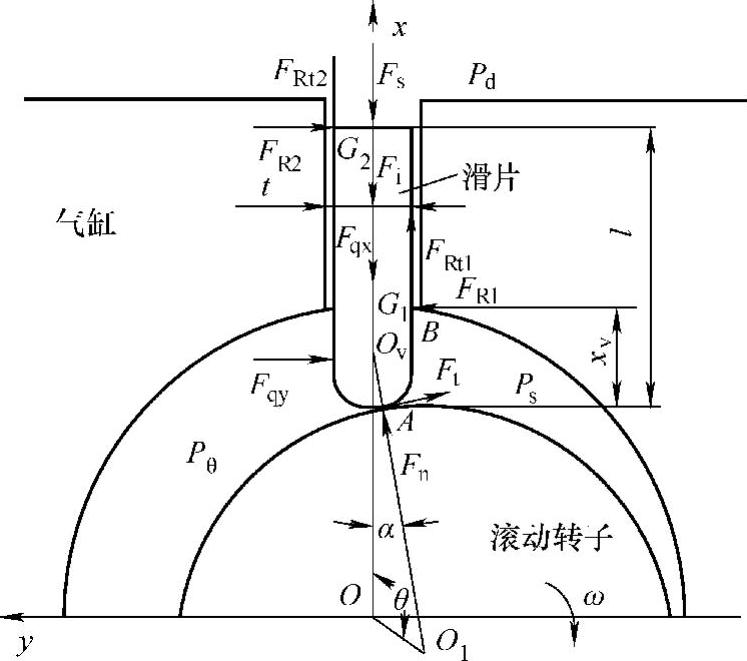
图3.17 滑片的受力
3)滑片上的油膜压力和气体压力。
根据理论计算和实验分析,滑片两侧所承受油膜压力随时间而变化,滑片两侧面与滑片槽并不总是接触。为便于分析,假设滑片两侧的油膜压力为线性分布,并且滑片两侧间隙内的压力相互抵消。
由图3.17可得到滑片x轴方向的气体力合力Fqx为
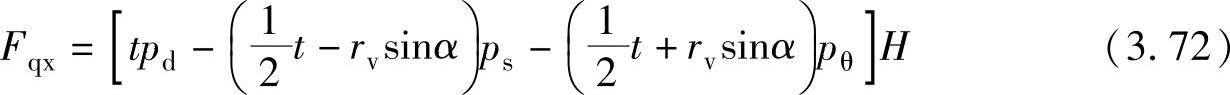
式中 t——滑片厚度,单位为m;
ps——吸气腔的气体压力,单位为Pa;
pθ——压缩腔的气体压力,单位为Pa;
pd——壳体腔内的气体压力,单位为Pa;
H——气缸的高度,单位为m。
滑片伸到气缸内的部分承受的气体压力合力Fqy为
Fqy=xv(pθ-ps)H (3.73)
式中 xv——滑片在气缸内的长度,单位为m。
4)滑片弹簧力。
作用在滑片上的弹簧力Fs为
Fs=Fs0+ks(2e-xv) (3.74)
式中 Fs0——xv=2e时的弹簧力,称为弹簧预紧力,单位为N;
ks——弹簧刚度系数,单位为N/m。
5)滑片往复惯性力。
滑片的往复惯性力大小和方向都在不断变化,往复惯性力会改变滑片与滚动转子外表面间的压力,当往复惯性力接近滚动转子表面方向时接触压力增大,使滑动滑片更加紧贴在滚动转子表面上;当往复惯性力远离滚动转子方向时接触压力减小,使滑片具有与滚动转子脱离的趋势。
滑片往复运动的往复惯性力Fi为
Fi=-mvav (3.75)
式中 mv——滑片的质量,单位为kg;
av——滑片往复运动的加速度,单位为m/s2。
6)摩擦力与正压力。
滑片与滚动转子及滑片槽之间的摩擦力和相应的正压力有以下关系:
Ft=μvFn (3.76)
式中 μv——滑片与滚动转子间的摩擦系数。
FRt1=μsFR1 (3.77)
式中 μs——滑片与滑片槽间的摩擦系数。
FRt2=μsFR2 (3.78)
在滚动转子式制冷压缩机中,由于受摩擦副的材料、表面状况、相对滑动速度、润滑状态等因素的影响,从理论上求得摩擦系数是非常困难的,需要通过试验获得。
沿x轴和y轴建立力平衡方程,有
FRt1+FRt2-Fi-Fs-Fqx+Fncosα+Ftsinα=0 (3.79)
FR1-Fqy-FR2+Fnsinα-Ftcosα=0 (3.80)
以滑片头部与滚动转子切点在滑片中心线上的投影点为中心建立力矩平衡方程(取顺时针方向为力矩的正方向),有
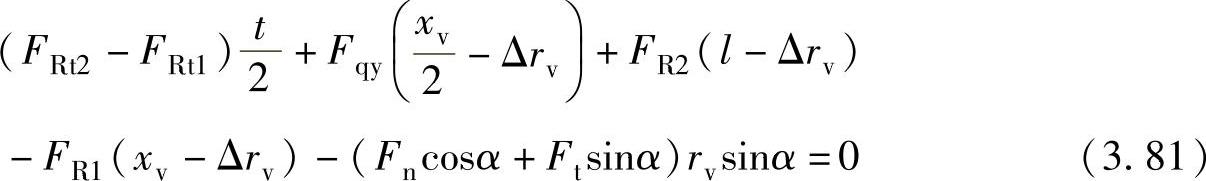
式中 l——滑片的长度,单位为m;
Δrv=rv(1-cosα)。
联立求解式(3.76)~式(3.81),得到
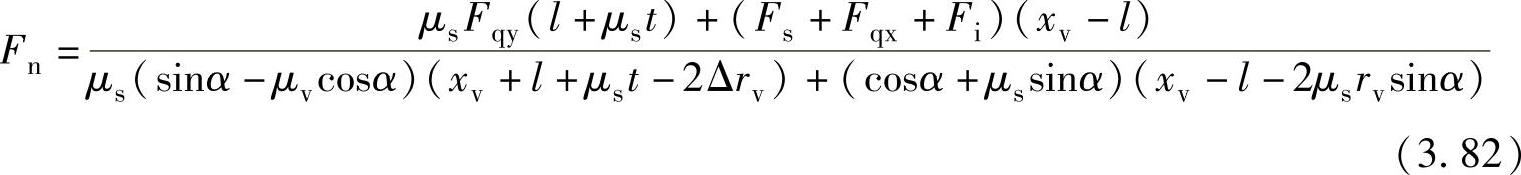
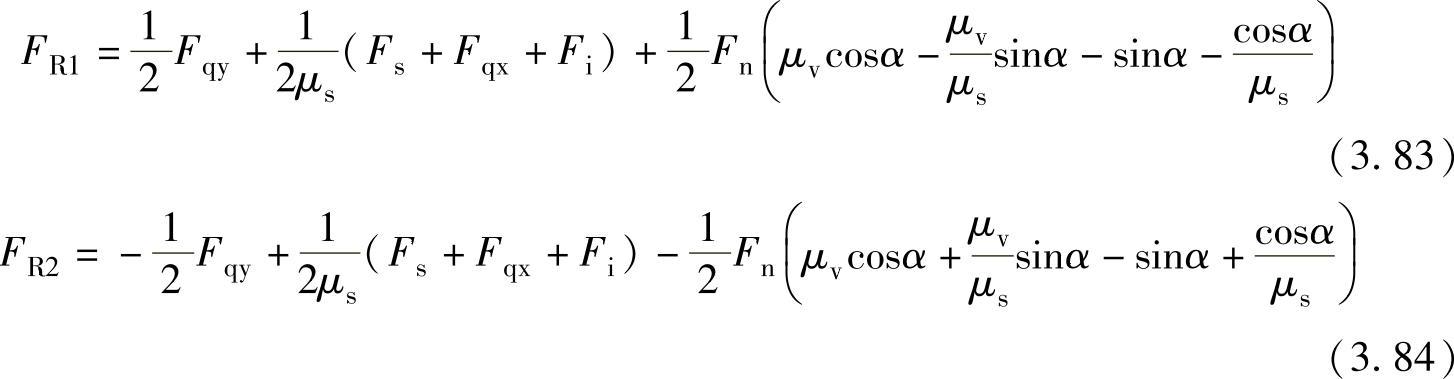
2.滚动转子的受力分析
压缩机运转时,滚动转子的运动为行星运动,它绕气缸中心点O作公转运动,绕自身中心点O1作自转运动,滚动转子随偏心轮轴的旋转做缓慢的转动,它自身转动的角速度要比偏心轮轴的角速度低很多。实际上,滚动转子瞬时角速度的大小和方向都是随时间变化的。
如图3.18所示,作用在滚动转子上的力和力矩有气体力Fg,滚动转子与滑片头部接触点A之间的摩擦力Fvt和径向力Fvn,滚动转子上下端面与气缸端盖间的摩擦力Fb1、Fb2和摩擦力矩Mb1、Mb2,滚动转子和气缸内壁接触点T之间的摩擦力Fct和摩擦力矩Ma,滚动转子和气缸液体动压产生的法向力Fcn,偏心轮轴对滚动转子内侧油膜压力Fen和粘滞力矩Mc,以及滚动转子旋转惯性力FIe。
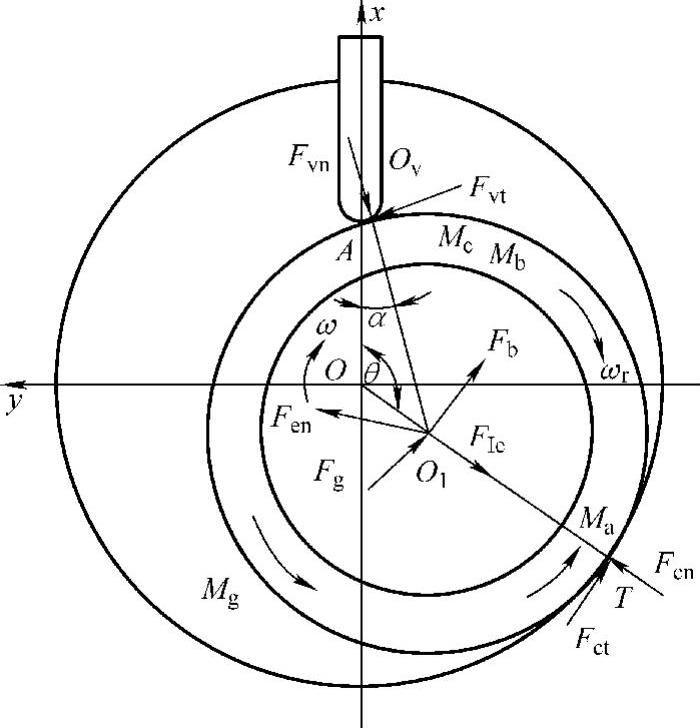
图3.18 滚动转子的受力
(1)气体力和气体力矩
气体力是指气缸内制冷剂气体压力作用在零部件上的力,它作用在气缸和端盖内表面、滚动转子外表面,以及滑片两侧和上下部端面。作用在滚动转上的气体力如图3.19所示,由压缩腔指向吸气腔。它作用的结果是产生轴承负荷,并使偏心轮轴弯曲。
由于作用在滚动转子上气体力的合力是通过滚动转子几何中心O1,而不是通过旋转中心O的,因而这一气体力会产生力矩。气体力产生的力矩是压缩机阻力矩的主要组成部分。
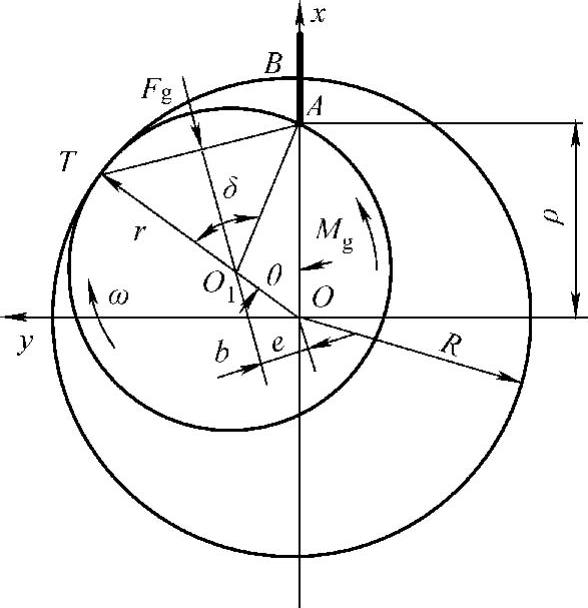
图3.19 作用在滚动转子上的气体力和力矩
如图3.19所示,设滚动转子在任一位置θ时,曲边三角形ABT内的气体处于压缩状态,其压力为pθ,而气缸工作容积的其他部分处于吸气状态,具有吸气压力ps。滚动转子外圆表面与AT弦平行方向的气体力相互抵消,在垂直于AT弦方向,气体力Fg为AT平面上的气体压力差产生的总合力,即

由于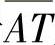 及pθ均随滚动转子转角θ的位置而变化,所以Fg的大小和方向也是变化的,但它始终指向滚动转子中心点O1。
及pθ均随滚动转子转角θ的位置而变化,所以Fg的大小和方向也是变化的,但它始终指向滚动转子中心点O1。
由图3.19中的几何关系可知
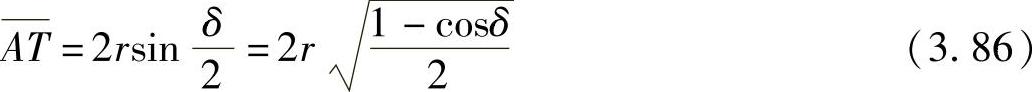
对于△AOO1,按余弦定理有
ρ2=r2+e2+2recosδ (3.87)
将式(3.65)代入式(3.87),并将根号按二项式定理展开,略去高次项有
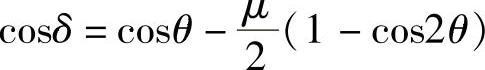
式中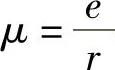 。
。
因此
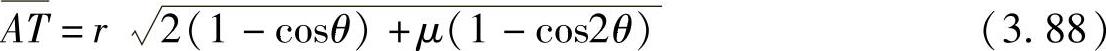
由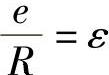 ,得r=R(1-ε),
,得r=R(1-ε),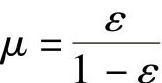 ,并将式(3.88)代入式(3.85)得到
,并将式(3.88)代入式(3.85)得到
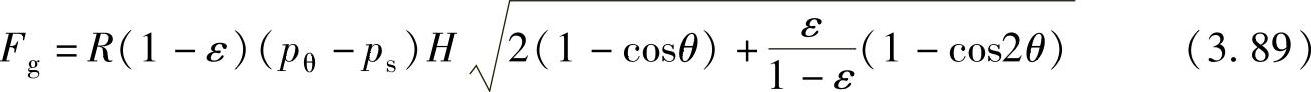
式中,pθ由式(3.19)计算。
根据式(3.89)计算得到的Fg-θ曲线如图3.20所示,从图3.20中可知,气体力合力的峰值出现在排气开始时,使用该曲线可以确定轴承的最大负荷以及滚动转子的最大弯矩。
由图3.19中可以看出,气体力合力的作用线并不通过旋转中心,因而会对旋转中心产生力矩,这种力矩称为气体力矩。由于它的作用方向与压缩机的旋转方向相反,是压缩机阻力矩的主要组成部分,因此,又称为气体阻力矩。
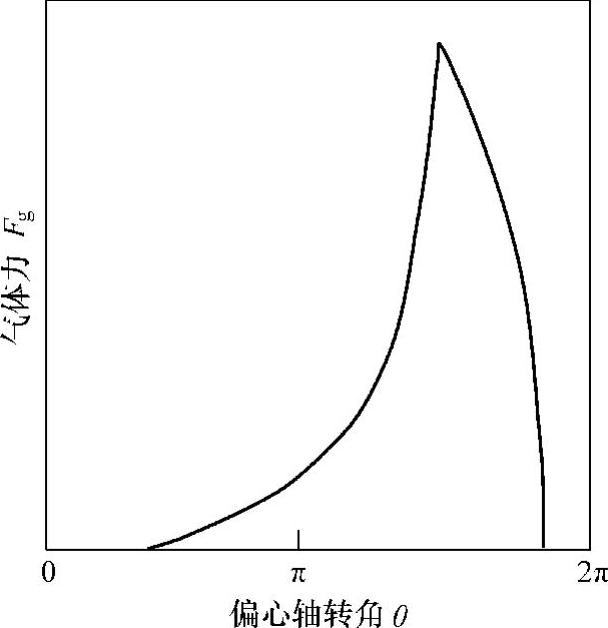
图3.20 气体力随转角的变化曲线
由图3.19可知,力臂长b为
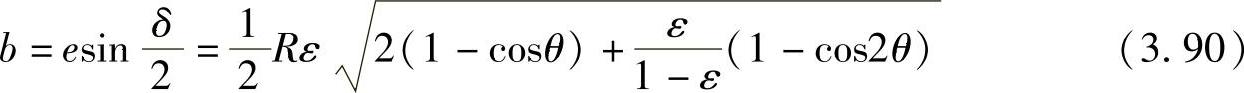
气体力力矩Mg等于力臂长度b与气体作用力Fg的乘积,即
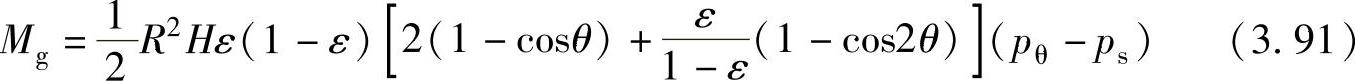
从式(3.91)中可以看出,气体阻力矩同样是随转角θ的变化而变化的,其峰值也是出现在排气开始的位置。
(2)滚动转子端面的粘性摩擦力和粘性摩擦力矩
1)滚动转子上端面的粘性摩擦力和粘性摩擦力矩。(https://www.daowen.com)
滚动转子上端部与气缸上端面之间充满润滑油,呈流体摩擦润滑状态,两者之间的间隙与滚动转子半径相比很小,故可采用大平板间流体润滑分析的方法。假设油层中速度线性分布,则有
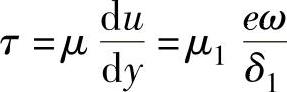
式中 μ1——润滑油的动粘度,单位为Pa·s;
δ1——滚动转子与气缸上端面之间的间隙,单位为m;
ω——偏心轮轴的角速度,单位为rad/s。
摩擦力Fb1为
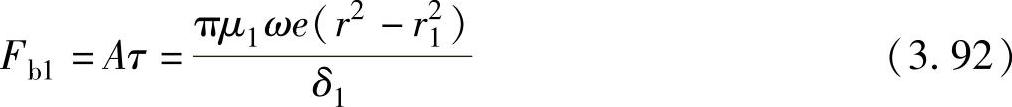
式中 A——滚动转子端部的面积,单位为m2;
r1——滚动转子内圆半径,单位为m。
当滚动转子以角速度ωr转动时,其端面半径rr处的速度为rrωr,因此有
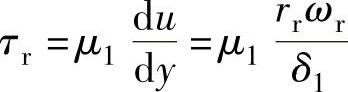
取微元环形面积dA=2πrrdrr,则在dA上产生的力矩Mb1为
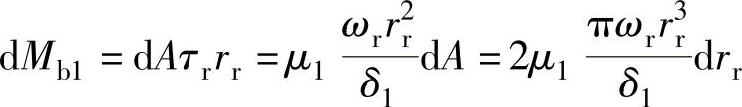
对上式积分,可以得到

2)滚动转子下端面的粘性摩擦力和粘性摩擦力矩。
与滚动转子与气缸上端面之间的摩擦状态相比,滚动转子与气缸下端面之间增加了滚动转子重量产生的摩擦力,并且摩擦状态由流体变为边界。滚动转子重量产生的粘性摩擦力Fb2g为
Fb2g=μ2mrg (3.94)
式中 mr——滚动转子的质量,单位为kg;
μ2——润滑油的动粘度,单位为Pa·s;
g——重力加速度,单位为m/s2。
滚动转子重量产生的粘性摩擦力矩Mb2g为
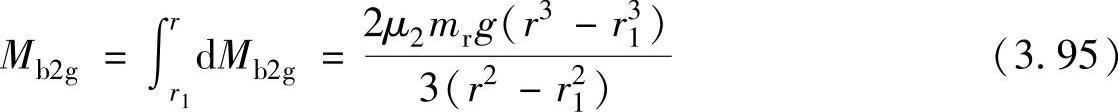
则滚动转子与气缸下端面之间的粘性摩擦力和粘性摩擦力矩分别为
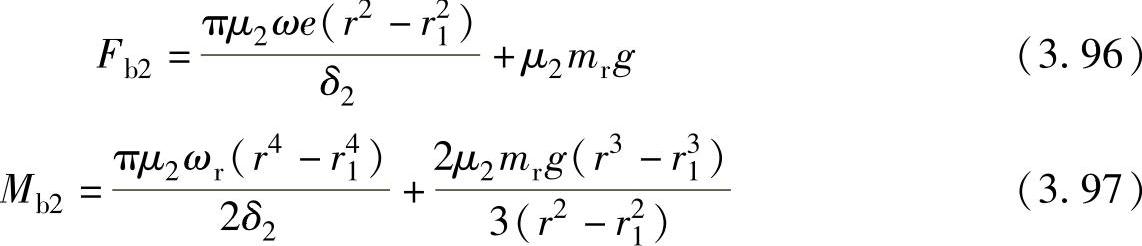
式中 δ2——滚动转子与气缸下端面之间的间隙,单位为m。
3)摩擦力合力与摩擦合力矩。
由式(3.92)、式(3.93)、式(3.96)和式(3.97)可以得到滚动转子与气缸上、下端面之间的摩擦合力和摩擦合力矩为
Fb=Fb1+Fb2(3.98)
Mb=Mb1+Mb2 (3.99)
(3)滚动转子与气缸内壁之间的摩擦力和摩擦力矩
滚动转子与气缸内壁之间的相对运动可以分为相对滑动和相对滚动,由于相对滚动产生的摩擦力较小,所以可忽略不计。滚动转子与气缸内壁之间为相对滑动,摩擦力Fct为

式中 μrc——润滑油的动粘度,单位为Pa·s;
v——滚动转子与气缸之间的相对滑动速度,v=eω+rωr;
δrc——滚动转子与气缸内壁之间的间隙,单位为m;
Lef——滚动转子与气缸内壁之间径向间隙的有效剪切长度,单位为m。
式(3.100)中
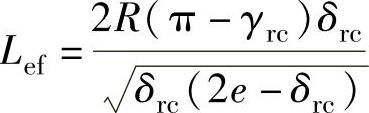
其中
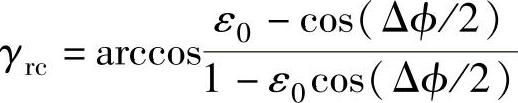
式中 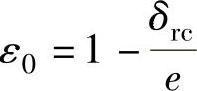 ;
;
Δϕ——径向间隙内密封油膜所占的角度。
滚动转子和气缸壁之间的摩擦力矩Ma为
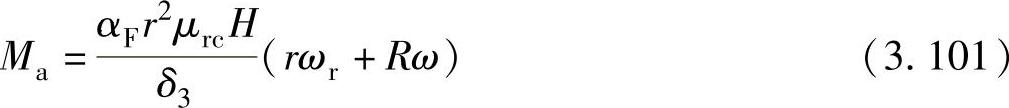
式中 αF——油膜弧度,单位为rad;
δ3——油膜的平均厚度,单位为m。
(4)滚动转子和气缸液体动压产生的法向力
滚动转子和气缸内壁之间产生的法向力可以分为两部分,即相对滑动和滚动产生的液体动压力和动压油膜压力。
滚动转子和气缸内壁之间相对滑动和滚动产生的液体动压力可以用Matin公式计算。在滚动转子和气缸内壁的最小径向间隙处,滚动转子的绝对速度为
u1=ωe+ωrr
气缸的绝对速度为
u2=0
最小间隙点,即接触点本身的绝对速度为
uc=ωR
形成流体动压效应的平均速度为
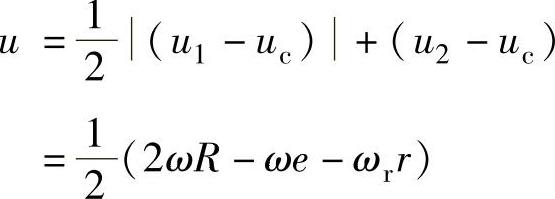
则滚动转子和气缸内壁相对滑动和滚动产生的流体动压力为
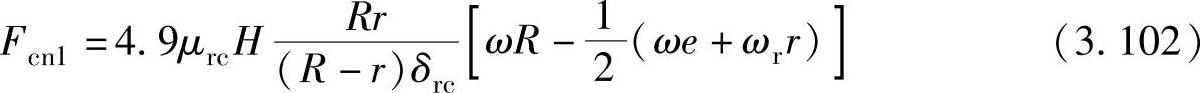
在压缩机运转过程中,气体压力不断变化,滚动转子和气缸内壁之间的径向间隙也不断变化。滚动转子和气缸内壁之间的相对运动在一定的相对速度下,由于润滑充分会形成良好的油楔,从而形成流体动力润滑,产生动压油膜压力,使承载能力大为提高,其值为
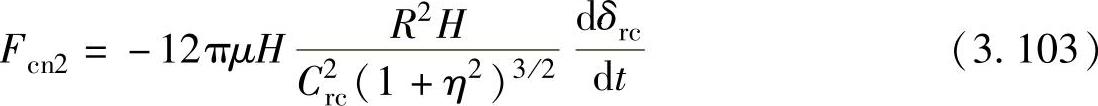
式中 Cre=e;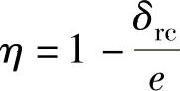 。
。
滚动转子与气缸内壁之间流体动压产生的法向力如下:
Fcn=Fcn1+Fcn2 (3.104)
(5)滚动转子轴承摩擦力矩
滚动转子与偏心轮轴轴颈组成轴承配合,由于作为轴承的滚动转子本身转动,并且作用轴承上载荷的大小和方向都不断变化,因而计算复杂。为了简便起见,假设偏心轮轴轴颈与滚动转子间隙内的油膜均匀,则根据润滑理论可以得到偏心轮轴轴颈与滚动转子之间的粘性摩擦力矩Mc为

式中 Re——偏心轮轴曲拐轴颈半径,单位为m;
le——偏心轮轴曲拐轴颈的长度,单位为m;
δe——滚动转子与偏心轮轴曲拐轴颈之间的间隙,单位为m;
ωr——滚动转子的角速度,单位为rad/s。
(6)滚动转子与滑片头部间的摩擦力和径向力
当滚动转子和滑片相对运动时,摩擦力为
Fvt=Fntμvr (3.106)
式中 Fvt——摩擦力,单位为N;
Fnt——径向力,单位为N;
μvr——摩擦系数。
摩擦力Fvt的方向与相对运行方向相反,径向力Fnt可由滚动转子运动方程求得。
滑片作用在滚动转子上的径向力Fnt产生的阻力矩为
Mn=-eFntsin(θ+α) (3.107)
式中的负号意味着Fnt在偏心轮轴前半转中产生驱动力矩,后半转中产生阻力矩。
(7)滚动转子的旋转惯性力和惯性力矩
由于滚动转子的质心不在旋转中心,所以旋转时将产生旋转惯性力,旋转惯性力的大小不变且始终指向偏心方向,如果滚动转子不平衡的质量为mx,其回转半径为rx,则当偏心轮轴转动的角速度为ω时,其旋转惯性力FIp为
FIp=mxrxω2 (3.108)
设偏心轮轴的角加速度为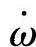 ,滚动转子绕旋偏心轮轴中心的转动惯量为JIp,则其惯性力矩为
,滚动转子绕旋偏心轮轴中心的转动惯量为JIp,则其惯性力矩为

(8)作用在偏心轴承上的载荷
在单个气缸中,作用在偏心轮轴承(又称转子轴承)上的力有作用在滚动转子上的气体力Fg;滑片作用在滚动转子上的法向力Fn通过滚动转子传递到偏心轮轴上;偏心轮轴曲拐的旋转惯性力FIe。作用在偏心轮轴承上粘性摩擦力矩有偏心轮轴曲拐与滚动转子之间的力矩Mc。
1)作用在偏心轴承上的载荷。
作用在偏心轴承上的载荷按照图3.18所示的坐标方向分解,有
x轴方向为
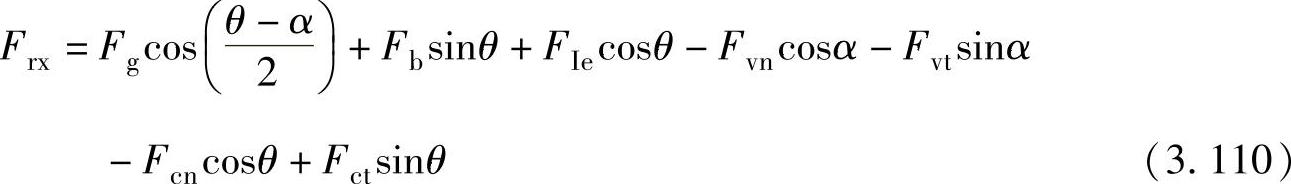
y轴方向为
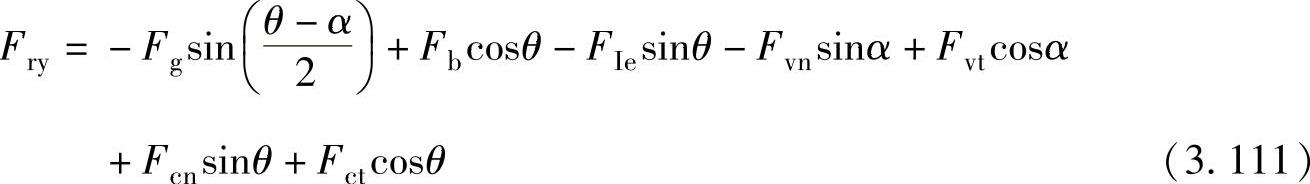
合力为

其方向

2)偏心轮轴承上粘性摩擦力矩。
由于滚动转子本身转动,并且作用在偏心轴承上载荷的大小和方向不断变化,所以粘性摩擦力矩计算复杂。为了简化计算,假设滚动转子与偏心轮轴曲拐轴颈的间隙是均匀的,则根据润滑理论得到滚动转子与偏心轮轴曲拐轴颈之间的摩擦力矩Mc,计算公式详见式(3.105)。
(9)滚动转子的运动微分方程
滚动转子的运动微分方程式为
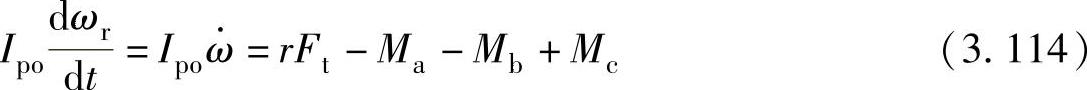
式中 Ipo——滚动转子的转动惯量,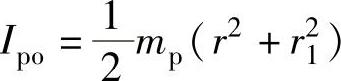 ,单位为kgm2;
,单位为kgm2;
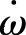 ——滚动转子的角加速度,单位为rad/s2。
——滚动转子的角加速度,单位为rad/s2。
用数值积分求解式(3.114),可以得到ωr的变化规律。近似计算时,可假设滚动转子为稳定工作状态,即滚动转子为匀速转动的自由体,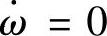 。由式(3.114)求得ωr的近似计算式为
。由式(3.114)求得ωr的近似计算式为
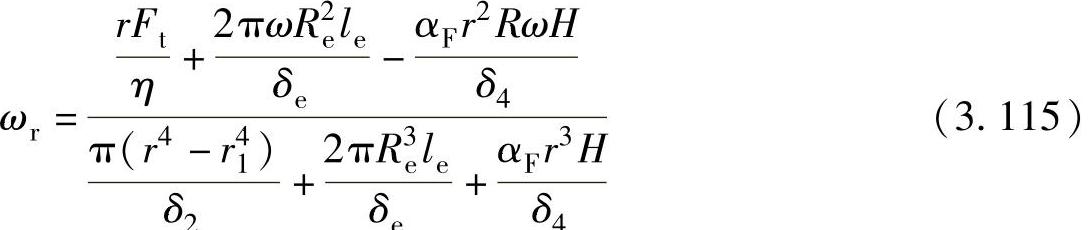
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





