地震仪所获得的实际地震波,一般含有一定意义的波形,又含有无意义的不规则的噪声,但从特定角度去描述,也可以将地震波视为不规则噪声的随机波,随机波在物理上的含义是像图3.4.1所示的一种极不规则的(相对于确定波而言)波形。但按第2章所述,如对这种随机波作一定的统计分析的话,仍能找到相应的规律。地震波在统计意义上而言,确实存在类似于满足各态历经而稳定(或不稳定)的随机波。
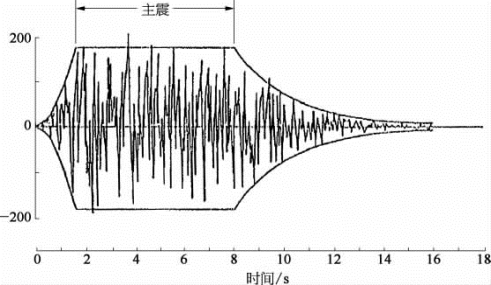
图3.4.1 随机地震波
当地震波满足各态历经的随机波时,则地震可以用第2章所述的功率谱密度变换表示。一般可以用以下两种方法描述。
1)地震波直接用功率谱密度方法表示
地震加速度![]() 数据所对应的功率谱密度函数可以通过地震加速度
数据所对应的功率谱密度函数可以通过地震加速度![]() 均方值的谱密度来描述数据的频率结构。也就是对于
均方值的谱密度来描述数据的频率结构。也就是对于![]() 样本时间历程记录在频率f到(f+Δf)范围内的均方值,可采用带通滤波特性的数字滤波器对样本记录进行滤波,然后计算出滤波器输出平方的平均值得到。当观察样本时间T趋于无穷大时,这一均方值将趋于正确的均方值。用公式可表示为
样本时间历程记录在频率f到(f+Δf)范围内的均方值,可采用带通滤波特性的数字滤波器对样本记录进行滤波,然后计算出滤波器输出平方的平均值得到。当观察样本时间T趋于无穷大时,这一均方值将趋于正确的均方值。用公式可表示为
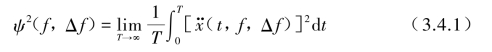
当频率间隔Δf非常小时,功率谱密度函数G(f)可定义为
![]()
更精确的定义可表示为
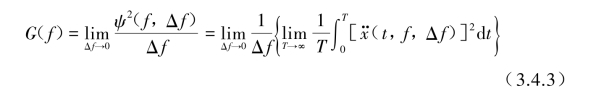
这里G(f)恒为单边实值非负函数。功率谱密度函数的一个重要性质是它与![]() 的自相关函数是傅里叶变换关系。为简易说明问题,以下均将脚标
的自相关函数是傅里叶变换关系。为简易说明问题,以下均将脚标![]() 略去。
略去。
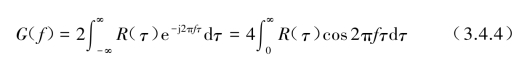
另一个是样本函数![]() 的均方根值与功率谱密度函数、自相关函数概率密度之间的关系:
的均方根值与功率谱密度函数、自相关函数概率密度之间的关系:
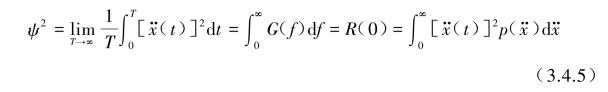
式(3.4.5)可理解为![]() 的均方值是功率谱密度G(f)曲线之下的总面积,也等于自相关函数R(τ)在原点τ=0时的值以及所有[
的均方值是功率谱密度G(f)曲线之下的总面积,也等于自相关函数R(τ)在原点τ=0时的值以及所有[![]() ]2在x··值上加权线性之和。
]2在x··值上加权线性之和。
这里要注意的是,功率谱密度在不同文献中有不同的表示方式。式(3.4.3)中G(f)称为“单边功率谱密度函数”,是在频率f所示的单边(f=0~∞)上表征为实值非负函数。另外也可用双边功率谱密度函数S(ω)来表示,以圆频率ω所示的双边(ω=-∞~∞)上表征为实值的非负函数。注意到这两种功率谱密度函数与相关函数之间的傅里叶变换与反变换关系,R(τ)对于τ为偶函数,单边功率谱密度G(f)与相关函数R(τ)为
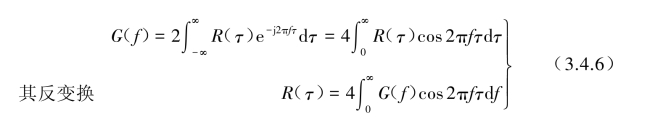
对于双边功率谱密度S(ω)则为
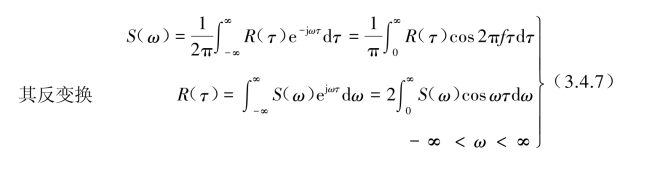
比较式(3.4.6)和式(3.4.7),可知G(f)与S(ω)关系为
G(f)=4πS(ω)
(3.4.8)
也有的文献资料将双边功率谱密度函数S(f)用频率f表示,其f的区域扩展为(-∞<f<∞)。这时S(f)与G(f)之间关系为
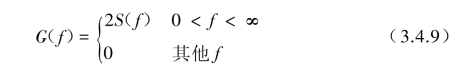
所以在使用中必须注意功率谱密度的定义以及横坐标上所使用的频率是f还是ω,如使用ω时,则G(f)和S(f)的关系(见图3.4.2)为
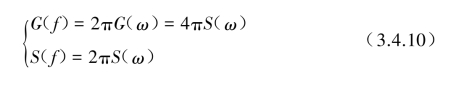
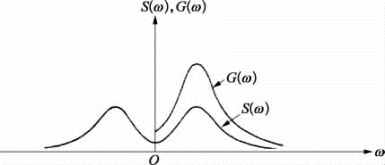
图3.4.2 功率谱密度函数
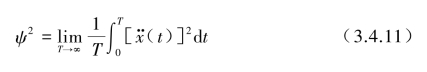
对于随机加速度![]() 的一个十分重要统计值均方值定义为在第2章中已证明
的一个十分重要统计值均方值定义为在第2章中已证明![]() 的均方值可用功率谱密度函数、自相关函数与概率密度函数表征:
的均方值可用功率谱密度函数、自相关函数与概率密度函数表征:
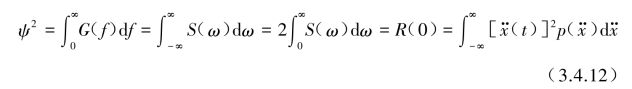 (https://www.daowen.com)
(https://www.daowen.com)
也可理解为![]() 时程曲线的均方值是功率谱密度函数G(f)[或S(ω)]曲线下的总面积,也等于自相关函数R(τ)在原点τ=0时R(0)值以及在
时程曲线的均方值是功率谱密度函数G(f)[或S(ω)]曲线下的总面积,也等于自相关函数R(τ)在原点τ=0时R(0)值以及在![]() 值上的加权线性之和。
值上的加权线性之和。
2)按三角级数模型合成地震波的方法
当平均值为零并是平稳高斯过程的![]() 时,可用三角级数模型模拟合成
时,可用三角级数模型模拟合成![]() :
:
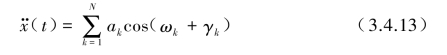
式中,ak是与已给出的功率谱密度函数S(ω)[或G(f)]有关的值。
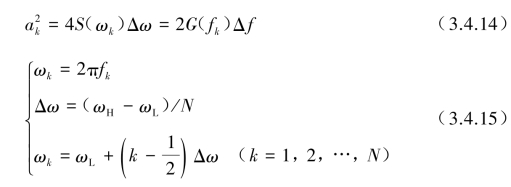
式中,ωH,ωL分别为高端处和低端处的频率,ak和γk对于k=1,2,…,N而言是相互独立不相关的变数。
可以证明式(3.4.14)的模型成立时,对任何N值,各态历程均能成立,其均值为
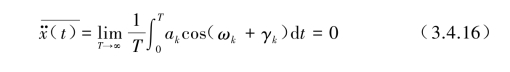
相关函数:
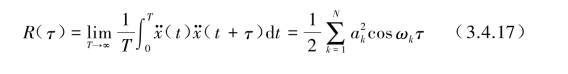
很容易证明,按式(3.4.12)得到![]() 的均方值为
的均方值为
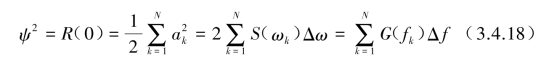
式(3.4.18)表示了均方值为功率谱密度函数沿圆频率ωk(或频率fk)所覆盖的面积(见图3.4.3)。
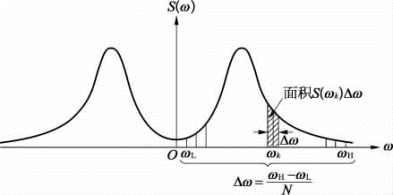
图3.4.3 功率谱密度函数的微段
对于非平稳地震加速度![]() ,常用的非平稳随机模型为
,常用的非平稳随机模型为
![]()
式中,![]() 是平均值为0的平稳高斯过程随机波,g(t)为一个确定性函数,在g(t)不为常数条件下,变量f(t)则为与g(t)的随时间变化过程相应的非平稳过程。
是平均值为0的平稳高斯过程随机波,g(t)为一个确定性函数,在g(t)不为常数条件下,变量f(t)则为与g(t)的随时间变化过程相应的非平稳过程。
式(3.4.19)的平均值为

自相关函数为
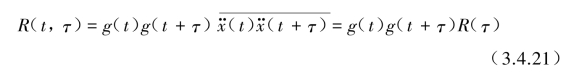
f(t)的均方值为τ=0的自相关函数:
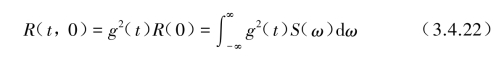
根据式(3.4.22),对f(t)的功率谱密度函数可表示为
S(t,ω)=g2(t)S(ω)
(3.4.23)
综上,对f(t)的模拟过程可取平稳随机过程的![]() 用三角级数表示为
用三角级数表示为
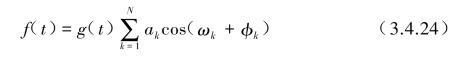
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






