为什么鲁尼每次接应射门都能解出二次方程？

“贝克汉姆开出任意球，为鲁尼划出了一条适时而完美的曲线……球进了！！！”

鲁尼是怎么做到的呢？你或许不会这么想，但要射进这样的球，他的数学一定好到不行。每一次接到贝克汉姆踢出的任意球，他都在下意识中解出了另一个伽利略所构架出来的方程式，即伽利略用来预测球体走势的公式。

方程式就像是食谱，我们找来一些食材，以某种特定方式把它们混合在一起，然后烹调出一道美味来。要构建出鲁尼所求解的公式，伽利略需要以下食材：足球离开贝克汉姆脚背时的水平速度u 和竖直速度v，重力的效果，即数字g的意涵，通过该数值，鲁尼便能确认这颗足球的竖直速度在每一秒的变化情况。而g的数值取决于球员置身的星球，在地球上，重力所产生的加速度为每秒9.8米/秒（约为22mph/秒）。伽利略的公式同时还告诉鲁尼，接球时球的高度与接球的位置是相关的。比如，如果足球位于距离贝克汉姆击球点x 米的距离，那么此时它距离地面的高度则为y 米：

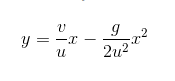
在这里，食材即一系列的数学指示，通过这些指示，我们知道如何运用这些数字，而最终的美食则是球体位于轨道中特定位置时的高度。

鲁尼若要确定出他应该站在多远的位置上，以将球踢进或顶进球门，他必须一步步向回求解，解出该方程。首先，假设他决定用头球进攻。鲁尼身高一米八零，因此球体的高度必须在y =1.80的高度他才可以顶到（不依靠起跳）。他知道u、v 及g的值。我们姑且取一些近似数值：

u =20, v =10, g =10

（速度u 和v 的单位为米/秒，加速度g的单位为米/秒²。）

鲁尼唯一不确定的是要站在离贝克汉姆多远的位置才能成功拦截到这个球。公式便将这一讯息编码在了其中，只是没那么明显罢了。根据公式，鲁尼应该站在距离贝克汉姆x 米的位置，而x 正是该公式中的未知数：

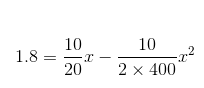
稍微调整一下，便可得出：

x²-40x +144=0

这类方程式大家应该很熟悉了，这就是我们都在学校学过的二次方程式。我们可以将其视为一个神秘填字游戏的线索，其中隐藏着x 的真实数值。

令人吃惊的是，最早求解此类方程的是古巴比伦人。他们的方程式并非用来描述足球的轨迹，而是为了测量幼发拉底河周边的土地。当我们试图确定某些自身与自身相乘的数值时便会遇到二次方程。之所以把这种运算称为平方是因为它会创造出一块正方区域，而这种二次方程的首次成型也的确是在计算一块土地面积的时候。

举一个典型例子。如果一个长方形区域的面积为55个平方单位，而该长方形的一条边比另一条边短6个单位，那么其中较长的那个边的边长是多少？在此，设长边的边长为x，可以得到x (x-6)=55，简化之后：

x²-6x-55=0

接下来，我们要如何解开这一数学密语呢？(https://www.daowen.com)

古巴比伦人想出了一个很简单的方法：他们将这一长方形切分开来，然后重新将碎片拼成一个正方形，后者相对容易处理。我们现在也可以像数千年前的巴比伦文书中所记载的那样来操作一下（如图5-2所示）。

首先，从长方形一端切下一块面积为3×(x-6)的小长方形，然后将其移至长方形的底端。整个长方形的面积并未改变，只是形状变了。新形状几乎就是一个边长为x-3个单位的正方形，但是，其中的一个角上缺了一个3×3的方块。如果将这个方块补齐，便是在原有面积的基础上增加了9个单位。因此，整个大区域的面积变为55+9=64。现在我们只需取64的平方根来表示正方形的边即可。于是x-3=8，x =11。尽管我们所做的只是在头脑中想象土地的切割和转移，但是，这一思想背后隐藏着此类隐秘二次方程式的一种通用解法。

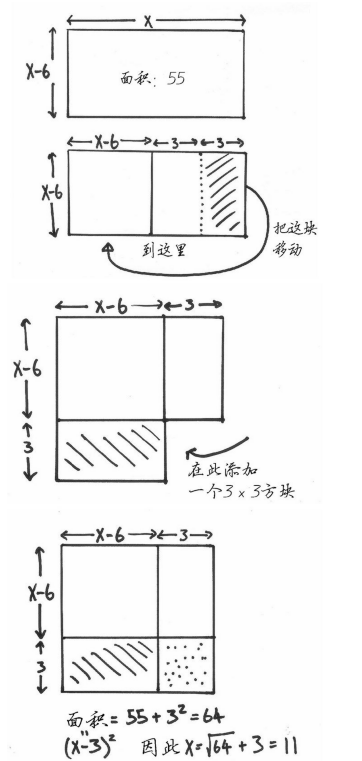
图 5-2　如何通过补全方块的方法来解二次方程式

自公元9世纪在伊拉克发明代数以来，巴比伦人的这一思想便可通过公式表述出来。代数这门学问是由巴格达智慧宫的院长穆罕默德·伊本·穆萨·花剌子密发展出来的。智慧宫是当时顶级的学术中心，世界各地的学者趋之若鹜，纷纷前往研习天文学、药学、化学、动物学、地理、炼金术、占星术以及数学等各种学问。穆斯林学者们收集并翻译了许多古代典籍，为子孙后代保存了这些文本，假如没有他们，恐怕我们也无法知晓希腊、埃及、巴比伦及印度的古代文明。但是，智慧院的学者们并不满足于仅仅翻译他人的数学理论，他们希望创造出属于他们自己的数学，以推动该学科的进一步发展。

实际上，在伊斯兰帝国初期的几百年中，求知欲是被积极提倡的。《古兰经》中有言，尘世间的知识能够拉近人们与圣贤知识之间的距离。实际上，伊斯兰教徒需要掌握数学技能，因为虔诚的穆斯林需要计算出祈祷的次数，及需要了解麦加的方向，以确定朝着哪个方向祈祷。

花剌子密的代数为数学带来了革命性的变化。代数是一门解释数字行为背后模式的语言，其中的语法决定着数字之间的交互方式。它有点像程序运行所需的编码，不管你把什么数字套进该程序中，它都能够运行。尽管古巴比伦人设计出了一种巧妙地解决特定二次方程式的方法，但是，正是花剌子密的代数公式才最终催生出了能够解出任何二次方程的公式。

这样一来，当你遇到一个二次方程式ax²+bx +c =0（其中a、b、c 为数字），只要通过几何式的杂耍，上述公式便可转换为方程左边为x，右边为一个包含数字a、b、c 的食谱配方：

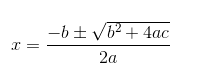
鲁尼正是通过上述公式来解出这一控制球体飞行的方程式的，并因而确定出他自己需要站在多远的地方才能接到球。我们刚才假定他要站在距离任意球踢出位置x 米远的地方，其中x 满足以下公式：

x²-40x+144=0

通过代数算法，即可求出x =36，因此，他应当站在离贝克汉姆36米的位置来顶这个球。

这是怎么算出来的呢？在表示贝克汉姆任意球曲线的方程式中，a =1，b =-40，c =144。因此，通过求解公式，我们可以算出距离：

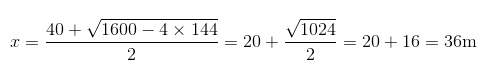
有趣的是，由于1024还有另外一个平方根-32，因此，我们还会得到另外一个结果：x=4米。该距离所对应的点是足球还在上升轨迹中的点，而鲁尼要知道的则是足球下落时的位置。因为在求平方根的过程中，我们总是会得到一正一负两个值，因此，通过上述公式求解时总会得到两个结果。为说明这一点，有时候我们会在根号前面放一个±标志，而非只有符号+。

当然，鲁尼更多靠的是直觉，因此，在长达90分钟的比赛中，他不需要一直做心算。但是，这仍显示出人类大脑在进化过程中获得了料事如神的能力。