单颗行星的偏心率起源于其运动之间的和谐比例的安排
第九章
单颗行星的偏心率起源于其运动之间的和谐比例的安排
因此我们发现,所有这六颗行星的普遍和谐比例都不可能出于偶然,特别是,除两颗行星是同时处于与普遍和谐比例最接近的和谐比例中的,所有的极运动都是与普遍和谐比例相吻合的。而且我们在第三卷通过和谐分割所确立的八度系统的所有音高也不大可能都由行星的极运动来指定;最不可能的是,天体的和谐被精妙地分成两种——大调和小调,会是出于偶然,而没有造物主的特殊关照。因此,一切智慧的源泉、秩序的坚定支持者、几何与和谐的永恒而超验的源泉——这位天体运动的造物主,一定是把起源于正平面图形的和谐比例与五种正立体形联系了起来,并从这两类形体当中塑造了一种最为完美的天的原型。正如六颗行星运动于其上的球体是通过五种正立体形来保证的一样,单颗行星的偏心率的度量也是通过从平面图形衍生出来的和谐比例(在第三卷中由它们导出)而被确定的,从而使行星的运动得以均衡匀称。为了使这两种东西可以产生出一种和谐比例,两球之间的较大比例应当在某种程度上屈从于偏心率的较小比例,这对于和谐比例的获得是必不可少的;因此,在和谐比例当中,那些与每一个立体形有较大亲缘关系的比例应当与行星相配。于是,它可以通过和谐比例而得来;通过这种方式,轨道的比例和单颗行星的偏心率最终都是从原型中同时产生出来的,而单颗行星的周期则是源于轨道的宽度和行星的体积。
当我力图通过几何学家所惯用的基本形式而使这种论证过程能够为人类的理智所把握的时候,愿天的创始者、理智之父、人的感觉的馈赠者、至圣而不朽的造物主能够阻止我心灵的黑暗带给这部著作任何配不上他的伟大的东西,愿他能使我们这些上帝的模仿者可以在生活的圣洁上来模仿他的作品的完美。为此,他在地球上选择了他的教堂,通过他儿子的血为它赎了罪,并在圣灵的帮助下,让我们远离一切不和谐的敌意、所有的纷争、敌对、愤怒、争吵、纠纷、宗派、忌妒、挑衅、令人恼火的玩笑以及人性的其他表现。所有那些拥有基督的精神的人不仅会同意我对这些事情的希望,而且会用行动去表达它们,担负起他们的使命,弃绝一切虚伪的举动,再也不用一种表面的热情、对真理的热爱、博学多才、在老师面前表现出来的谦虚或任何其他虚伪的外衣来包装它了。神圣的父啊!让我们永远彼此相爱,以使我们能够合为一体,就像您与您的儿子——我们的主、圣灵合而为一一样,就像您已使您的一切作品通过最为美妙的和谐的纽带合而为一一样。通过使您的臣民和谐一致,您的教堂就可以在地球上耸立起来,就像您从和谐之中构建了天本身一样。
先验的理由
1.公理。下面这种说法是合理的:无论在什么地方,只要有可能,单颗或两颗行星的极运动之间必定已经建立起了一切种类的和谐,以使那种变化可以为世界增辉。
2.公理。六个球之间的五个间距必定在一定程度上对应着五种正立体的内切球和外接球之比,顺序与立体形本身的自然次序相同。
关于这一点,参见第一章、《宇宙的奥秘》和《哥白尼天文学概要》第四卷。
3.命题。地球与火星之间的距离,以及地球与金星之间的距离同它们的球相比必定是最小的,并且大致是相等的;土星和木星之间的距离,以及金星与水星之间的距离居中,并且同样大致相等;而木星与火星之间的距离则是最大的。
由公理2,在位置上对应于几何球体比例最小的立体形的行星得出的比例也应该最小;对应于居间比例的立体形的行星得出的比例也应该居间;而对应于最大比例的立体形的行星得出的比例也应该最大。十二面体和二十面体之间的次序与火星与地球、地球与金星之间的次序是相同的;立方体和八面体之间的次序与土星和木星、金星和水星之间的次序是相同的;最后,四面体的次序与木星和火星之间的次序是相同的(参见第三章)。因此,最小的比例将会在地球与火星、地球与金星之间存在,而土星和木星之间的比例大致等于金星和水星之间的比例;最后,木星和火星之间的比例是最大的。
4.公理。所有行星都应当有不同的偏心率和不同的黄纬运动,它们与太阳这个运动之源的距离也和偏心率一样各有不同。
由于运动的本质不在于存在而在于生成,所以某一颗行星在运行过程中所穿过的区域的样子或形状并非从一开始就成为立体的,而是随着时间的推移,最后不仅要求长度,而且也要求宽度和深度,形成完整的三维;渐渐地,通过很多圈的交织和积聚,一种凹陷的球形就显现了出来——就像蚕丝在交织和缠绕很多圈后结成蚕茧一样。
5.命题。每一对相邻行星必定被指定了两种不同的和谐比例。
因为根据公理4,每颗行星与太阳之间都有一个最大距离和一个最小距离,所以根据第三章,每颗行星都有最慢的运动和最快的运动。因此,存在着两种极运动之间的主要比较,一种是两颗行星的发散运动,另一种是它们的收敛运动。它们必定彼此不同,因为发散运动的比例会大一些,收敛运动的比例会小一些。但不同的行星对之间必定存在着不同的和谐比例,以使这种多样能够为世界增辉(根据公理1);还因为根据命题3,两颗行星之间的距离的比例是不同的。但球与球之间的每一个确定的比例都因其量的关系而对应着和谐比例,一如本卷第五章中所证明的那样。
6.命题。两个最小的和谐比例4 : 5和5 : 6在行星对之间不会出现。
因为5 : 4 = 1000 : 800,6 : 5 = 1000 : 833,但十二面体与二十面体的外接球与内切球之比都是1000 : 795,这两个比例标明了彼此距离最近的行星球之间的距离,或者说最小间距。因为对其他立体形来说,外接球与内切球之间的距离要更大。然而,根据第三章第十三条,如果偏心率与球之间的比例不是太大的话,那么这里运动之比仍然要大于距离之比。[1]因此,运动之间的最小比例大于4 : 5和5 : 6。因此,这些和谐比例事实上已为正立体形所排除,从而不会在行星间出现。
7.命题。除非行星极运动之间的固有比例复合起来之后大于一个纯五度,否则两颗行星的收敛运动之间不会出现纯四度的协和音程。
设收敛运动之比为3 : 4。首先,假设没有偏心率,单颗行星的运动之间没有固有的比例,而收敛运动和平均运动是相同的,那么相应的距离(根据这个假设,它就是球的半径)就等于这个比例的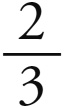 次方,即4480 : 5424(根据第三章)。但这个比例已经小于任何正立体形的两球之比了,所以整个内球将被内接在任何一个外球的正立体形的表面所切分。但这与公理2是相违背的。
次方,即4480 : 5424(根据第三章)。但这个比例已经小于任何正立体形的两球之比了,所以整个内球将被内接在任何一个外球的正立体形的表面所切分。但这与公理2是相违背的。
其次,设极运动之间的固有比例的复合是某个确定的值,并设收敛运动之比是3 : 4或75 : 100,但相应距离之比是1000 : 795,因为没有正立体形有更小的两球之比。由于运动之比的倒数要比距离之比大750 : 795,所以如果按照第三章的原理,把这份盈余除以1000 : 795,那么得到的结果就是9434 : 7950,即为两球之比的平方根。因此这个比例的平方,即8901 : 6320或10000 : 7100,就是两球之比。把它除以收敛距离之比1000 : 795,得到的结果为7100 : 7950,大约为一个大全音。平均运动与两个收敛运动之间形成的两个比例的复合必须至少足够大,以使收敛运动之间可以形成纯四度。因此,发散极距离与收敛极距离之间的复合比大约是这个比例的平方根,即两个全音;而收敛距离之比是它的平方,即比一个纯五度稍大。因此,如果两颗临近行星的固有运动的复合小于一个纯五度,那么其收敛运动之比就不可能是纯四度。
8.命题。和谐比例1 : 2和1 : 3,即八度和八度加五度,应属于土星和木星。
因为根据本卷第一章,它们获得了正立体形中的第一个——立方体,是第一级的行星和最高的行星;根据本书第一卷中的说法,这些和谐比例在自然的秩序中是排在最前列的,在两大立体形家族——二分或四分的立体形以及三分的立体形——中是首领。[2]然而,作为首领的八度1 : 2略大于立方体的两球之比1 : 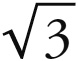 ;因此,根据第三章第13条,它适合成为立方体行星的运动的较小比例,而1 : 3则作为较大比例。
;因此,根据第三章第13条,它适合成为立方体行星的运动的较小比例,而1 : 3则作为较大比例。
然而,这个结论还可通过以下方式得到:如果某个和谐比例与正立体形的两球之比之间的比例与从太阳上看到的视运动与平均距离之比相等,那么这个和谐比例就会被理所当然地赋予运动。但是很自然地,根据第三章结尾的内容,发散运动之比应当远大于两球之比的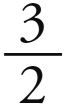 次方,也就是说,近乎于两球之比的平方,而且1 : 3是立方体两球之比1 :
次方,也就是说,近乎于两球之比的平方,而且1 : 3是立方体两球之比1 : 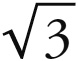 的平方,因此,土星与木星的发散运动之比是1 : 3(关于这些比例与立方体的许多其他关系,参见前面第二章)。
的平方,因此,土星与木星的发散运动之比是1 : 3(关于这些比例与立方体的许多其他关系,参见前面第二章)。
9.命题。土星和木星的极运动的固有比例的复合应当约为2 : 3,一个纯五度。
这个结论由前一命题可以得出;这是因为,如果木星的近日运动是土星的远日运动的三倍,而木星的远日运动是土星的近日运动的两倍,那么把1 : 2除以1 : 3,得到的结果就是2 : 3。
10.公理。如果可以在其他方面进行自由选择,那么较高的行星的运动的固有比例应当在本性上就是优先的,或是更加卓越的,甚或是更加伟大的。[3]
11.命题。土星的远日运动与近日运动之比是4 : 5,一个大三度;而木星的远日运动与近日运动之比则是5 : 6,一个小三度。
因为当它们复合起来之后等于2 : 3,但2 : 3只能被和谐分割为4 : 5和5 : 6。因此,和谐的作曲家上帝和谐地分割和谐比例2 : 3,(根据公理1)把它的较大的、更好的大调的男性的和谐部分给了土星这个较大较高的行星,而把较小的比例5 : 6给了较低的行星木星(根据公理10)。
12.命题。金星和水星应当具有1 : 4这个大的和谐比例,即两个八度。
因为根据本卷第一章,立方体是初级形体的第一个,八面体是次级形体的第一个。而从几何上考虑,立方体在外面,八面体在里面,即后者可以内接于前者,所以在宇宙中,土星和木星是外行星的起始,或者说是最外层的行星;而水星和金星则是内行星的起始,或者说是最内层的行星;八面体则被置于它们的路径之间:参见第三章。因此,在这些和谐比例中,必定有一个初级的,并且与八面体同源的和谐比例属于金星和水星。而且,依照自然次序紧随1 : 2和1 : 3之后的和谐比例是1 : 4,它与立方体的和谐比例1 : 2是同源的,因为它也是从同一组图形即四边形中产生的,而且与1 : 2是可公度的,因为它等于1 : 2的平方;而八面体也与立方体同族,且与之可公度。而且,1 : 4由于一个特别的原因而与八面体同源,即4这个数在这个比例中,而一个正方形隐藏在八面体当中,正方形的内接圆与外接圆之比是1 : 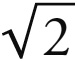 。
。
因此,和谐比例1 : 4是这个比例的平方的连续幂,即1 : 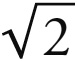 的四次方(参见第二章)。于是,1 : 4应当属于金星和水星。由于在立方体中,1 : 2是两颗最外行星的较小的和谐比例,因为这里是最外层的位置;所以在八面体中,1 : 4将是两颗最内行星的较大的和谐比例,因为这里是最内层的位置。但1 : 4在这里之所以被赋予较大的和谐比例而不是较小和谐比例,还有以下的原因。[4]因为八面体的两球之比是1 :
的四次方(参见第二章)。于是,1 : 4应当属于金星和水星。由于在立方体中,1 : 2是两颗最外行星的较小的和谐比例,因为这里是最外层的位置;所以在八面体中,1 : 4将是两颗最内行星的较大的和谐比例,因为这里是最内层的位置。但1 : 4在这里之所以被赋予较大的和谐比例而不是较小和谐比例,还有以下的原因。[4]因为八面体的两球之比是1 : 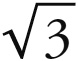 ,如果假定八面体在行星中的镶嵌是完美的(尽管它实际上不是完美的,而是略微穿过了水星天球——这对我们是有利的),那么,收敛运动之比必定小于1 :
,如果假定八面体在行星中的镶嵌是完美的(尽管它实际上不是完美的,而是略微穿过了水星天球——这对我们是有利的),那么,收敛运动之比必定小于1 : 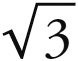 的
的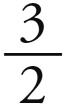 次方;但是1 : 3就是1 :
次方;但是1 : 3就是1 : 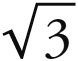 的平方,于是就比真正的比例大,而比1 : 3还要大的1 : 4也要比真正的比例大,所以即使是1 : 4的平方根也不可能是收敛运动之比。[5]因此,1 : 4不可能是较小的八面体比例,而应是较大的。
的平方,于是就比真正的比例大,而比1 : 3还要大的1 : 4也要比真正的比例大,所以即使是1 : 4的平方根也不可能是收敛运动之比。[5]因此,1 : 4不可能是较小的八面体比例,而应是较大的。
此外,1 : 4与八面体的正方形同源,正方形的内接圆与外接圆之比是1 : 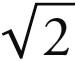 ,正如1 : 3与立方体同源,立方体的外接球和内切球之间的比例为1 :
,正如1 : 3与立方体同源,立方体的外接球和内切球之间的比例为1 : 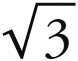 一样。正像1 : 3是1 :
一样。正像1 : 3是1 : 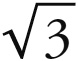 的幂次,即它的平方一样,这里1 : 4也是1 :
的幂次,即它的平方一样,这里1 : 4也是1 : 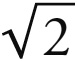 的幂次,即它的四次方。因此,如果1 : 3是立方体的较大和谐比例(根据命题7),那么1 : 4就应当成为八面体的较大和谐比例。
的幂次,即它的四次方。因此,如果1 : 3是立方体的较大和谐比例(根据命题7),那么1 : 4就应当成为八面体的较大和谐比例。
13.命题。木星与火星的极运动应当具有如下和谐比例:一个是较大的和谐比例1 : 8,即三个八度,另一个是较小的和谐比例5 : 24,即两个八度加一个小三度。
因为立方体已经得到了1 : 2和1 : 3,而位于木星和火星之间的四面体的两球之比1 : 3等于立方体两球之比1 : 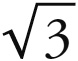 的平方。因此,数值等于立方体比例的平方的运动之比应当属于四面体。但1 : 2和1 : 3的平方为1 : 4和1 : 9,而1 : 9不是和谐比例,1 : 4已经被用在了八面体上。因此,根据公理1,这就必须要用到与这些比例临近的和谐比例。在这些相邻比例当中,首先遇到的较小比例是1 : 8,较大比例是1 : 10。到底应该选择这两个比例中的哪个,则要根据它们与四面体的亲缘关系决定。虽然1 : 10属于五边形组,但这与五边形没有任何共同之处。但四面体由于多方面的原因而与1 : 8有更大的亲缘关系(参见第二章)。
的平方。因此,数值等于立方体比例的平方的运动之比应当属于四面体。但1 : 2和1 : 3的平方为1 : 4和1 : 9,而1 : 9不是和谐比例,1 : 4已经被用在了八面体上。因此,根据公理1,这就必须要用到与这些比例临近的和谐比例。在这些相邻比例当中,首先遇到的较小比例是1 : 8,较大比例是1 : 10。到底应该选择这两个比例中的哪个,则要根据它们与四面体的亲缘关系决定。虽然1 : 10属于五边形组,但这与五边形没有任何共同之处。但四面体由于多方面的原因而与1 : 8有更大的亲缘关系(参见第二章)。
此外,下列理由也倾向于1 : 8:正如1 : 3是立方体的较大和谐比例,1 : 4是八面体的较大和谐比例一样(因为它们是这两个立体形的两球之比的幂次),1 : 8也应是四面体的较大和谐比例,因为正如第一章中所说的,四面体的体积是内接于它的八面体的二倍,所以八面体比例中的8是四面体比例中的4的二倍。
再有,正如立方体的较小和谐比例1 : 2是一个八度,八面体的较大和谐比例1 : 4是两个八度,所以四面体的较大和谐比例1 : 8就应该是三个八度。而且,更多的八度应该属于四面体而不是立方体和八面体,这是因为,由于四面体的较小的和谐比例必定要大于其他立体形的较小的和谐比例(因为四面体的两球之比是所有立体形中最大的),所以四面体的较大和谐比例也要超过其他立体形的较大和谐比例几个八度。最后,三个八度音程与四面体的三角形形式有亲缘关系,而且与三位一体的普遍完美性相一致,因为甚至三个八度的项8,也是完美的量即三维的第一个立方数。
与1 : 4或6 : 24相临近的一个较大的和谐比例是5 : 24,一个较小的和谐比例是6 : 20或3 : 10。然而,3 : 10属于五边形组,而与四面体没有任何共同之处。但5 : 24却因3和4(从中产生出12和24)而与四面体有亲缘关系。因为我们这里忽略了其他较小的项,即5和3,正如我们在第二章中所看到的,它们与立体形的同源程度是最小的,而且,四面体的两球之比是3 : 1,根据公理2,收敛距离之比也应当大致与此相等。根据第三章,收敛运动之比大约等于距离的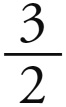 次方之比的倒数,而3 : 1的
次方之比的倒数,而3 : 1的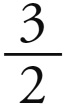 次方约等于1000 : 193。因此,如果取火星的远日运动为1000,则木星的近日运动将略大于193,但会远小于1000的三分之一即333。因此,木星和火星的收敛运动之间的和谐比例不是10 : 3即1000 : 333,而是24 : 5即1000 : 208。
次方约等于1000 : 193。因此,如果取火星的远日运动为1000,则木星的近日运动将略大于193,但会远小于1000的三分之一即333。因此,木星和火星的收敛运动之间的和谐比例不是10 : 3即1000 : 333,而是24 : 5即1000 : 208。
14.命题。火星极运动的固有比例应大于3 : 4这个纯四度,而大约等于18 : 25。
设木星和火星被赋予了精确的和谐比例5 : 24和1 : 8或3 : 24(命题13)。把较大的5 : 24的倒数与较小的3 : 24复合,得到结果3 : 5。而前面的命题11说过,木星本身的固有比例是5 : 6。再把这个比例的倒数与3 : 5复合,即把30 : 25与18 : 30进行复合,得到的结果就是火星的固有比例18 : 25,它大于18 : 24或3 : 4。但如果考虑到接下来的原因,即较大的共有比例1 : 8还要更大,那么它还会变得更大。
15.命题。和谐比例2 : 3即五度、5 : 8即小六度、3 : 5即大六度将依次被分配给火星和地球、地球和金星、金星和水星的收敛运动。
因为介于火星、地球和金星之间的十二面体和二十面体具有最小的外接球和内切球之比,所以它们应当具有可能的和谐比例中最小的,这样才能同源,而且也使公理2得到满足。但是根据命题4,所有和谐比例中最小的5 : 6和4 : 5是不可能的,因此,这些立体形应当具有大于它们的最近的和谐比例3 : 4、2 : 3、5 : 8或3 : 5。
介于金星和水星之间的八面体的两球之比与立方体是一样的。但根据命题8,立方体收敛运动之间的较小和谐比例是八度。因此,如果没有其他数值介入,那么根据类比,八面体的较小和谐比例也应是同一数值,即1 : 2。但如下数值介入了进来:如果把立方体行星,即土星和木星的运动的固有比例复合起来,那么结果将不大于2 : 3;而如果把八面体行星,即金星和水星的固有比例复合起来,结果就将大于2 : 3。原因很显然:假定我们所需要的是立方体和八面体之间的比例,设较小的八面体比例大于这里给出的比例,而与立方体的比例1 : 2一样大;但根据命题12,较大的和谐比例是1 : 4。因此,如果把它用我们已经假设的较小的和谐比例1 : 2去除,那么得到的结果1 : 2仍将是金星和水星的固有比例的复合。但1 : 2大于土星和木星的固有比例的复合2 : 3。根据第三章,这个较大的复合的确会导致一个较大的偏心率;但同样根据第三章,这个较大的偏心率又会导致收敛运动之间的一个较小比例。因此,通过把这个较大的偏心率乘以立方体与八面体之间的比例,我们就得到金星和水星的收敛运动之间也需要一个小于1 : 2的比例。不仅如此,根据公理1,由于立方体行星的和谐比例是八度,所以另一个与此非常接近的和谐比例(根据较早的证明,它小于1 : 2)应当属于八面体行星。比1 : 2略小的比例是3 : 5,作为三者之中最大的,它应当属于两球之比最大的立体形,即八面体。因此,较小的比例5 : 8、2 : 3或3 : 4就被留给了两球之比较小的二十面体和十二面体。
这些余下的比例是这样在剩下的两颗行星中进行分配的。因为在这些立体形当中,尽管两球之比相等,但立方体得到了1 : 2这个和谐比例,八面体则得到了较小的和谐比例3 : 5,以使金星和水星的固有比例的复合能够超过土星和木星的固有比例的复合;所以尽管十二面体与二十面体的两球之比相等,但前者应当拥有一个比后者更小但相当接近的和谐比例,原因是类似的:因为二十面体介于地球和火星之间,而且如前所述有一个大的偏心率;而正如我们在下面将会看到的,金星和水星却有着最小的偏心率。由于八面体的和谐比例是3 : 5,二十面体的两球之比较小,具有比3 : 5稍小的紧接着的比例5 : 8,因此,留给十二面体的或者是余下的2 : 3,或者是3 : 4;但更可能的是与二十面体的5 : 8较为接近的2 : 3,因为它们是类似的立体形。
但3 : 4的确不可能。因为尽管如前所述,火星的极运动之比足够大,但地球——正如已经说过的,并将在下面阐明的——贡献的固有比例太小,以至于不足以使两个比例的复合超过一个纯五度。因此,根据命题7,3 : 4不可能有自己的位置。这更是因为——由下面的命题17可得——收敛运动之比必定大于1000 : 795。
16.命题。金星和水星的固有运动之比的复合大约为5 : 12。
把命题15赋予这对行星的较小和谐比例3 : 5除以较大比例1 : 4或3 : 12(根据命题12),得到的结果5 : 12就是两颗行星固有比例的复合。所以水星的极运动的固有比例要比金星的固有比例5 : 12小。这可以通过这些第一类的理由来理解。根据下面的第二类理由,通过把两颗行星共有的和谐比例当作一种“酵母”包括进来,我们就会看到,只有水星的固有比例才是5 : 12。
17.命题。火星与地球的发散运动之间的和谐比例不可能小于5 : 12。
根据命题14,只有火星的固有运动比例超过了纯四度,大于18 : 25。但根据命题15,它们较小的和谐比例是纯五度。因此,这两部分的复合为12 : 25。但根据公理3,地球也必须具有自己的固有比例。因此,由于发散运动的和谐比例是由以上这三种组分构成的,所以它将大于12 : 25。但接下来的一个比12 : 25即60 : 125稍大的和谐比例是5 : 12即60 : 144。因此,根据公理1,如果这两颗行星的运动的较大比例需要一个和谐比例,那么它不可能小于60 : 144或5 : 12。
因此,至此为止,根据目前所说的公理,除了只有地球和金星这一对行星仅仅被分配了一个和谐比例5 : 8之外,其余所有行星对都出于必然理由而得到了两个和谐比例。因此,我们现在必须重新开始进一步探索它的另一个和谐比例,即较大的或发散运动的和谐比例。
后验的理由
18.公理。运动的普遍和谐比例必定是由六种运动的相互调节,特别是通过极运动来确立的。
由公理1可以证明。
19.公理。在运动的一定范围内,普遍和谐比例必须是一样的,以使它们能够出现得更加频繁。
如果它们被局限于运动的个别的点,那么它们就有可能永远也不出现,或者出现得非常少。
20.公理。正如第三卷已经证明的,由于对和谐比例种类(generum)的最自然的区分是大调和小调,所以两种普遍和谐比例必须在行星的极运动之间获得。
21.公理。两种和谐比例的不同种类必须被确立,以使世界的美可以通过所有可能的变化形式来展现;这只能通过极运动,或至少是通过某些极运动来实现。
由公理1可得。
22.命题。行星的极运动必已指定了八度系统的音高或音符,或者音阶中的音符。
正如第三卷已经证明的,基于一个共有音符的和谐比例的起源和比较产生了音阶,或者说把八度分成了它的音高或音符。因此,由于根据公理1、20和21,极运动之间需要有不同的和谐比例,所以某个天的系统或和谐音阶需要通过极运动来做出真正的划分。
23.命题。必定有这样一对行星,其运动之间的和谐比例只存在大六度3 : 5和小六度5 : 8。
根据公理20,和谐比例的种类之间存在着必然的区分。根据命题22,这种区分是通过拱点处的极运动来实现的,因为要想排列和整理它们,只有极运动——最快的和最慢的运动——才需要被确定,各种居间的调子都是当行星从最慢运动到最快的过程中自行产生的,它们不需要任何特别的关照。因此,只有当两颗行星的极运动之间形成了一个第西斯或24 : 25时,这种排列才可能发生,因为如第三卷中所解释的,和谐比例的不同种类之间相差一个第西斯。
然而,第西斯或者是4 : 5和5 : 6这两个三度之间的差距,或者是3 : 5或5 : 8这两个六度之间的差距,或者是再升高一个或几个八度之后的这些比例之间的差距。但是根据命题6,4 : 5和5 : 6这两个三度在行星对之间并不出现;而且除了火星和地球这对行星的5 : 12(与之相关的只有2 : 3) ,[6]增加一个八度的三度或六度也没有出现。所以居间的比例5 : 8、3 : 5和1 : 2都同样是容许的。因此,余下的两个六度3 : 5和5 : 8要被给予一对行星。而且它们运动的变化只能是六度,以至于它们既不会扩张到下一个较大的音程2 : 1,即一个八度,也不会缩小为下一个较小的音程2 : 3,即一个五度。这是因为,尽管如果两颗行星的收敛极运动之间构成一个纯五度,发散运动之间构成一个八度,那么同样的两颗行星也的确可以构成六度,从而跨过一个第西斯,但这却不能体现运动的规定者的天道。因为那样一来,最小的音程第西斯——它潜藏于极运动之间所包含的所有大音程之中——就会被随着调子连续变化的居间运动所超越,但它不是由它们的极运动决定的,因为部分总是小于整体的,即第西斯总要小于介于2 : 3和1 : 2之间的较大音程3 : 4,这里,后者将被认为是由极运动所确定的。
24.命题。改变了和谐比例种类的两颗行星应当在它们极运动的固有比例之间形成一个第西斯,其中一个的固有比例将大于一个第西斯;它们的远日运动之间应当形成一个六度,近日运动之间应当形成另一个六度。
由于极运动之间构成了两个相距为一个第西斯的和谐比例,这可以以三种方式来产生:或者一颗行星的运动保持不变,另一颗的运动变化一个第西斯;或者当上行星在远日点,下行星在近日点时,两者都变化半个第西斯,构成一个大六度3 : 5,并且当它们移出那些音程彼此相互靠近,上行星运动到近日点,下行星运动到远日点时,它们构成一个小六度5 : 8;或者最后一种可能,在从远日点向近日点运动的过程中,一颗行星比另一颗行星的变化更大,从而超过一个第西斯,于是这两颗行星在远日点的运动之间就形成了一个大六度,在近日点的运动之间就形成了一个小六度。但第一种方式是不合法的,因为那样一来,这些行星中的某一颗将没有偏心率,从而与公理4相违背。第二种方式不那么美,也不那么适宜:之所以不美,是因为不够和谐,两颗行星的运动的固有比例将不是悦耳的,因为任何一个小于第西斯的音程都是不协和的。然而,让某一颗行星受到这个不协和的小音程的影响会好一些。事实上,它是不可能发生的,因为如果是这种方式,那么极运动就会偏离系统的音高或音阶的音符,从而与命题22相违背;它之所以是不适宜的,是因为六度只在行星分别位于相反的拱点时的那些运动中出现。如果是这样,那么这些六度以及从它们当中导出的普遍和谐比例就不可能有地方产生。因此,当行星的所有和谐位置都被局限在它们轨道上的几个有限的个别的点时,普遍和谐比例将会极为稀少,从而与公理19相违背。因此,还剩下第三种方式,即每一颗行星都变化自己的运动,但其中一颗要比另一颗变化大,而且至少要相差一个完整的第西斯。
25.命题。对于改变和谐种类的两颗行星来说,上行星的固有运动的比例应当小于一个小全音9 : 10;而下行星的固有比例则应小于一个半音15 : 16。
根据前一命题,它们或是通过远日运动,或是通过近日运动来构成3 : 5的比例。但通过近日运动是不可能的,因为那样一来,它们的远日运动之比就将是5 : 8。因此,根据同一命题,下行星的固有比例将比上行星高出一个第西斯,但这是与公理10相违背的。因此,它们只能通过远日运动构成3 : 5的比例,近日运动构成的是5 : 8的比例,后者比前者小了24 : 25。然而,如果远日运动构成了一个大六度3 : 5,那么上行星的远日运动与下行星的近日运动之间将构成一个超过大六度的音程,这是因为下行星将复合其整个固有比例。
同样地,如果近日运动构成一个小六度5 : 8,那么上行星的近日运动和下行星的远日运动将构成一个小于小六度的音程,因为下行星将复合其整个固有比例的倒数。然而,如果下行星的固有比例等于一个半音15 : 16,那么除了六度以外,纯五度也可以出现,因为一个小六度减去一个半音就成了一个纯五度,但这是与命题23相违背的。因此,下行星的固有音程将小于一个半音。由于上行星的固有比例要比下行星的固有比例大一个第西斯,而一个第西斯加上一个半音就成了一个小全音9 : 10,因此,上行星的固有比例小于一个小全音9 : 10。
26.命题。对改变和谐种类的两颗行星来说,上行星的极运动之间所构成的音程应当或者是一个第西斯的平方576 : 625,即大约12 : 13,或者是半音15 : 16,或者是与前者或后者相差音差80 : 81的某个居间的音程;而下行星应当或者是一个纯粹的第西斯24 : 25,或者是一个半音与一个第西斯之差125 : 128,即大约42 : 43,或者最后,是与前者或后者相差音差80 : 81的某个居间的音程,也就是说,上行星应当构成第西斯的平方减去一个音差,下行星构成一个纯粹的第西斯减去一个音差。
根据命题25,上行星的固有比例应当大于一个第西斯,根据前一命题,它应当小于一个小全音9 : 10。但事实上,根据命题24,上行星应当超过下行星一个第西斯。和谐之美告诉我们,即使这些行星的固有比例由于过小而不可能是和谐的,根据公理1,如果可能,它们至少也应当是协和的。但是,小于小全音9 : 10的协和音程只有两种,即半音和第西斯,但它们彼此之间相差不是一个第西斯,而是一个更小的音程125 : 128。因此,上行星不可能具有一个半音,下行星也不可能具有一个第西斯;或者上行星具有一个半音15 : 16,下行星具有125 : 128,即42 : 43,或者下行星具有一个第西斯24 : 25,上行星具有第西斯的平方,即约为12 : 13。但由于两颗行星是平权的,所以即使协和的性质不得不在它们的固有比例中被打破,它也必须在两者中被均等地打破,从而使它们的固有音程之差仍将是一个精确的第西斯,根据命题24,这对于区分和谐比例的种类是必要的。如果上行星的固有比例小于第西斯的平方的量或者超过一个半音的量,等于下行星的固有比例小于一个纯粹的第西斯的量或者超过125 : 128这个音程的量,那么协和的性质就会在两者中被均等地打破。
不仅如此,这种盈余或亏缺必定是一个音差,即80 : 81,因为为了使音差在天体运动中被表达的方式能够像在和谐比例中一样,即通过彼此之间的音程的盈余或亏缺来表达,和谐比例不能指定任何其他音程。因为在协和音程中,音差是大小全音之差,它不以任何其他方式出现。
接下来我们需要探究的是,在那些被提出的音程中,哪些是更可取的。是第西斯(下行星的纯粹第西斯和上行星的第西斯的平方),还是上行星的半音和下行星的125 : 128?回答是第西斯,论证如下:因为尽管半音已经在音阶中以不同方式表示过了,但与之相关的比例125 : 128还没有被表示。另一方面,第西斯已经以不同方式表示过了,第西斯的平方也以一种方式表示了,即把全音分解为第西斯、半音和小半音;那样一来,正如第三卷第八章中已经说过的,两个第西斯大约相距两个音高。另一种论证是,第西斯是可以对种类进行分类的,而半音却不行。因此,相对于半音来说,我们必须给予第西斯更多的关注。总而言之,上行星的固有比例应当是2916 : 3125,大约为14 : 15,下行星的固有比例应当是243 : 250,大约为35 : 36。
你或许会问,至高的造物主的智慧可能像这样沉湎于如此细致而费力的计算吗?我回答说,可能有许多原因对我是隐藏着的。但是如果和谐的本性没有提供更有分量的理由(因为我们正在处理的比例小于所有协和音程所能容许的范围),那么认为上帝甚至连这些理由也遵循了,无论它们显得有多么琐碎,这也并非愚蠢,因为他从不规定任何没有缘由的东西。相反,宣称上帝选取这些量是随机性的(它们都小于为它们规定的界限——小全音)倒是愚蠢的。说他之所以把它们取成那样的量,是因为他愿意这样选择,这样说也是不充分的。因为对那些可以进行自由选择的几何事物来说,上帝做出的任何选择都有某种几何上的原因,正如我们可以在叶边、鱼鳞、兽皮、兽皮上的斑点以及斑点的排列等诸如此类的东西上所看到的那样。
27.命题。地球与金星的较大运动比例应该是远日运动之间的大六度;较小的运动比例应该是近日运动之间的小六度。
根据公理20,区分和谐比例的种类是必要的。但是根据命题23,只有通过六度才可能做到这一点。因为根据命题15,地球和金星这两个相邻的二十面体行星已经得到了小六度5 : 8,所以另一个六度3 : 5也应当指派给它们。但是根据命题24,它不是在收敛极运动或发散极运动之间形成,而是在同侧的极运动之间形成,即远日运动之间形成一个六度,近日运动之间形成另一个六度。此外,和谐比例3 : 5与二十面体同源,因为两者都属于五边形组。参见第二章。
这就是精确的和谐比例可以在这两颗行星的远日运动和近日运动之间找到,而不能在收敛运动之间找到的原因(正如上行星的情况那样)。
28.命题。地球的固有比例大约为14 : 15,金星的固有比例大约为35 : 36。
根据前一命题,这两颗行星必定区分了和谐比例的种类。因此,根据命题26,地球作为上行星应该得到音程2916 : 3125,大约为14 : 15,而金星作为下行星则应得到音程243 : 250,大约为35 : 36。
这就是这两颗行星具有如此之小的偏心率,以及由此导出的极运动之间的小音程或固有比例的原因,尽管比地球高的下一颗行星火星以及比金星低的下一颗行星水星具有最大的偏心率。天文学证明了这一点的真实性。因为我们在第四章中看到,地球的比例是14 : 15,金星是34 : 35,天文学的精确度几乎无法把它与35 : 36区分开。[7]
29.命题。火星与地球运动的较大和谐比例,即发散运动的和谐比例不可能是那些大于5 : 12的和谐比例中的一个。
根据上面的命题17,它不是小于5 : 12的比例中的任何一个;但是现在,它也不是大于5 : 12的比例中的任何一个。因为这些行星的另一个较小的共有比例2 : 3与火星的固有比例(根据命题14,它将大于18 : 25)进行复合,得到的结果将会大于12 : 25即60 : 125。把它与地球的固有比例14 : 15即56 : 60(根据前一命题)进行复合,得到的结果将会大于56 : 125,大约为4 : 9,也就是说略大于一个八度加一个大全音。而下一个比八度加全音更大的和谐比例是5 : 12,即八度加小三度。
请注意,我并没有说这个比例既不大于也不小于5 : 12,而是说如果它必定是和谐的,那么没有其他和谐比例会属于它。
30.命题。水星运动的固有比例应当大于所有其他行星的固有比例。
根据命题16,金星和水星的固有运动复合起来大约为5 : 12。但是金星自己的固有比例是243 : 250,即1458 : 1500。把它的倒数与5 : 12即625 : 1500进行复合,那么得到的结果625 : 1458就是水星自己的固有比例,它大于一个八度加一个大全音,而其余行星中固有比例最大的行星——火星的固有比例小于2 : 3,即一个纯五度。
事实上,如果把金星与水星这两颗最低的行星的固有比例复合在一起,那么得到的结果将大致等于四颗较高行星的固有比例的复合。因为正如我们马上就会看到的,土星和木星的固有比例的复合超过了2 : 3,火星的固有比例小于2 : 3,把这两个比例复合起来,得到4 : 9即60 : 135。再把它与地球的14 : 15即56 : 60复合起来,得到的结果为56 : 135,它略大于5 : 12,而正如我们刚刚看到的,5 : 12是金星与水星的固有比例的复合。然而,这既不是被追求到的,也不是取自任何分立的、特殊的美的原型,而是通过与业已确立的和谐比例相关的原因的必然性自发出现的。
31.命题。地球的远日运动与土星的远日运动之间的和谐比例必定是若干个八度。
根据命题18,普遍和谐比例是必定存在的,因此土星与地球、土星与金星之间也必定存在着和谐。但如果土星的其中一种极运动既不与地球的极运动保持和谐,也不与金星的极运动保持和谐,那么根据公理1,与土星的两种极运动都与这些行星保持和谐相比,这样的和谐将会更少。因此,土星的两种极运动应该都与地球和金星保持和谐:其远日运动与其中一颗行星保持和谐,其近日运动与另一颗行星保持和谐,因为它是第一颗行星的运动,不存在什么阻碍。因此,这些和谐比例将或者同音[8](identisonae)或者不同音(diversisonae),即或者是连续加倍比例,或者是其他比例。但其他比例是不可能的,因为在3和5(根据命题27,它们确定了地球与金星的远日运动之间的较大和谐比例)这两项之间无法建立两个调和平均值;因为六度无法被分成三个音程(参见第三卷)。因此,土星的两种运动不可能与3和5的调和平均值构成一个八度;但为了使它的运动能够与地球的3和金星的5之间形成和谐,它的一种运动必须与已经提到的行星之一构成同音的和谐比例,或者相差若干个八度。由于同音和谐比例更加卓越,所以它们也必须在更加卓越的极运动即远日运动之间建立起来,这既是因为它们因行星的高度而占据着卓越的位置,也是因为地球和金星把和谐比例3 : 5(我们把它处理为较大的和谐比例)当成了它们的固有比例和某种意义上的特权。虽然根据命题27,这个和谐比例也属于金星的近日运动和地球的某种居间的运动,但它开始是在极运动中形成的,居间的运动则是在这之后。
我们一方面有最高的行星土星的远日运动,另一方面,与之相配的必须是地球的远日运动而非金星的远日运动,因为在这两颗区分了和谐种类的行星当中,地球是较高的行星。还有一个更加直接的原因:后验的理由——我们现在正在讨论的——实际上修正了先验的理由,不过只是对最小的地方进行了修正,因为它是一个有关小于所有协和音程的音程的问题。但根据先验的理由,不是金星的远日运动,而是地球的远日运动接近于与土星的远日运动之间建立起来的几个八度的和谐比例。因为如果把:1)土星运动的固有比例,即土星的远日运动与近日运动之比4 : 5(根据命题11),2)土星与木星的收敛运动之比,即土星的近日运动与木星的远日运动之比1 : 2(根据命题8),3)木星与火星的发散运动之比,即木星的远日运动与火星的近日运动之比1 : 8(根据命题14),4)火星与地球的收敛运动之比,即火星的近日运动与地球的远日运动之比2 : 3(根据命题15)这几项复合起来,那么你就会发现,土星的远日运动与地球的近日运动之间的复合比例为1 : 30,它比1 : 32或五个八度仅仅小了30 : 32,即15 : 16或一个半音。因此,如果一个被分成了比最小的协和音程还小的各个部分的半音与这四个组分相复合,那么土星和地球的远日运动之间就会形成一个完美的五个八度的和谐比例。然而,要想使土星的同一远日运动与金星的远日运动之间能够形成若干个八度,那么根据先验的理由,从中拿掉大约一个纯四度是必要的。因为如果把地球与金星的远日运动之比3 : 5同前面四种组分构成的比例1 : 30复合起来,那么根据先验的理由,我们发现土星与金星的远日运动之比是1 : 50,这个音程与五个八度1 : 32相差32 : 50,即16 : 25或纯五度加一个第西斯;与六个八度1 : 64相差50 : 64,即25 : 32或纯四度减一个第西斯。因此,同音和谐比例必定要被建立起来,不过不是建立在金星与土星的远日运动之间,而是建立在地球与土星的远日运动之间,以使土星可以保持一种与金星不同音的和谐比例。
32.命题。在行星的小调的普遍和谐比例中,土星精确的远日运动与其他行星之间不可能形成精确的和谐比例。
地球的远日运动并不与小调的普遍和谐比例相一致,因为地球和金星的远日运动之间构成了大调的音程3 : 5(根据命题27),而土星的远日运动与地球的远日运动之间构成了一个同音的和谐比例(根据命题31)。因此,土星的远日运动与它也不一致。不过,土星在非常接近于远日点的地方有一种稍快的运动,它非常接近于小调——我们已经在第七章中很清楚地看到了这一点。
33.命题。大调的和谐比例和大音阶与远日运动密切相关,而小调的和谐比例和小音阶与近日运动相关。
虽然大调的和谐比例(dura harmonia)不仅在地球的远日运动与金星的远日运动之间形成,而且也在地球比远日点低的运动和金星比远日点低的运动(直到近日点)之间形成;另一方面,小调的和谐比例不仅在金星的近日运动和地球的近日运动之间形成,而且也在金星比近日点高的运动(直到远日点)和地球比近日点高的运动之间形成(根据命题27);但是,对这些种类的和谐比例的指定只属于每颗行星的极运动(根据命题20和24)。因此,大音阶只被指定给远日运动,小音阶只被指定给近日运动。
34.命题。大音阶与两颗行星中的上行星的关系更近,小音阶则与下行星的关系更近。
因为大音阶是远日运动所固有的,小音阶是近日运动所固有的(根据上一命题),而远日运动比近日运动更慢,也更低沉,因此,大音阶是较慢的运动所固有的,小音阶是较快的运动所固有的。但两颗行星中的上行星与较慢的运动更加相关,下行星与较快的运动更加相关,因为固有运动的快慢总是与行星在世界中的高度相伴随的。因此,在同时具有两种调式的两颗行星中,上行星与大音阶的关系更近,下行星则与小音阶的关系更近。而且,大音阶使用了大音程4 : 5和3 : 5,小音阶使用了小音程5 : 6和5 : 8。但是,上行星既有一个更大的天球和更慢的运动,也有一个更长的轨道;那些在两方面都符合的东西是彼此更加亲近的。(https://www.daowen.com)
35.命题。土星和地球与大音阶的关系更近,而木星和金星则与小音阶的关系更近。
首先,与金星一起指定两种音阶的地球是上行星。因此,根据上一命题,地球主要包含大音阶,金星主要包含小音阶。而根据命题31,土星的远日运动与地球的远日运动之间构成了一个八度的和谐比例,因此,根据命题33,土星也包含大音阶。其次,根据命题31,土星因其远日运动而更加青睐大音阶,而且根据命题32,排斥小音阶。因此,较之小音阶,它与大音阶的关系更为密切,因为音阶是被极运动指定的。
木星与土星相比是下行星。由于大音阶属于土星,所以根据上一命题,小音阶应当属于木星。
36.命题。木星的近日运动与金星的近日运动必定在同一音阶上相一致,但构不成和谐比例,而与地球的近日运动就更不可能构成和谐比例了。
根据前一命题,木星主要与小音阶相关,而根据命题33,近日运动与小音阶密切相关,因此,木星通过其近日运动必定指定了小音阶,也就是说指定了它的确定音高或主音(phthongum)。但是根据命题28,金星的近日运动与地球的近日运动也指定了同一音阶,因此,木星的近日运动将与它们的近日运动在同一个音阶中相关联。但它不可能与金星的近日运动之间建立和谐比例,因为根据命题8,它应当与土星的远日运动,即木星的远日运动是G音的那个系统的d音构成1 : 3的和谐比例,但金星的远日运动是e音,因此,它与e音之间的差距在最小的和谐比例所对应的音程之内。最小的和谐比例是5 : 6,但d音和e音之间的音程还要小很多,即9 : 10,一个全音。尽管金星在近日点的音要高于远日点的e音,但这种提高要小于一个第西斯(根据命题28)。然而,如果把一个第西斯(因此还包括那些更小的音程)与一个小全音复合,那么结果还不到最小的和谐比例5 : 6所对应的音程。因此,木星的近日运动不可能既与土星的远日运动之间构成1 : 3或接近1 : 3的比例,同时又与金星保持和谐。它也不能与地球保持和谐,因为如果木星的近日运动已经被调整到金星的近日运动的同一音阶,以至于它能与土星的远日运动之间形成1 : 3的音程,差距小于最小的音程,也就是说与金星的近日运动之间相差一个小全音9 : 10或36 : 40(再加上几个八度),而地球的近日运动与金星的近日运动之间相差5 : 8即25 : 40,那么地球和木星的近日运动之间将相差25 : 36(再加上几个八度)。但这不是和谐比例,因为它是5 : 6的平方,或一个纯五度减去一个第西斯。
37.命题。土星与木星的固有复合比例2 : 3,以及它们较大的共有和谐比例1 : 3必须增加一个等于金星[固有]音程的音程。
根据命题27和命题33,金星的远日运动有助于指定大音阶,近日运动有助于指定小音阶。而根据命题35,土星的远日运动也应当与大音阶一致,从而与金星的远日运动一致。但是根据上一命题,木星的近日运动与金星的近日运动之间也要一致。因此,金星的远日运动与近日运动之间的音程有多大,与土星的远日运动形成1 : 3比例的木星的近日运动也应当加上多大。但是根据命题8,木星与土星的收敛运动之间的和谐比例是精确的1 : 2。因此,如果从音程1 : 2中减去这个大于1 : 3的音程,那么得到的大于2 : 3的结果就是这两颗行星的固有比例的复合。
在前面的命题28中,金星运动的固有比例是243 : 250,约为35 : 36。但是在第四章中我们看到,土星的远日运动与木星的近日运动之间所构成的比例要比1 : 3略大,这个大出来的量介于26 : 27与27 : 28之间。但是如果把一秒——我不知道天文学能否探测到这个差别——加在土星的远日运动上,那么这两个量就完全相等了。
38.命题。到目前为止通过先验的理由建立起来的土星和木星的固有比例的复合2 : 3的盈余因子243 : 250,必须以这样的方式被分配到行星中去:其中的一个音差80 : 81给土星,余下的19683 : 2000或约为62 : 63的比例给木星。
由公理19可得,这个因子必须在两颗行星中分配,以使每颗行星都能在一定程度上与同它相关的普遍和谐比例相一致。但是,音程243 : 250小于所有的协和音程。因此,没有和谐规则能够把它分成两个协和的部分,除了在前面命题26中划分第西斯24 : 25时需要的音程,即把它分成一个音差80 : 81(这是那些小于协和音程的音程中最主要的一个[9])和略大于一个音差的19683 : 20000,约为62 : 63。然而,要分离的不是两个音差,而是一个音差,以免各个部分太不相等,因为土星和木星的固有比例非常接近于相等(根据公理10,甚至会扩展到那些比它们还小的协和音程),还因为音差是由一个大全音和一个小全音所确定的音程,而两个音差却不是。而且,尽管土星有着较大的固有和谐比例4 : 5,但属于土星这颗更高更大的行星的必定不是那个较大的部分,而是那个优先的、更美的即更和谐的部分。因为根据公理10,优先性与和谐的完美性是首先要考虑的,而对量的考虑可以放在最后,因为量本身是没有美可言的。于是,正如我们在第三卷第十二章中对它的称法,土星的运动变为64 : 81,即一个掺杂[10]大三度,而木星的运动变为6561 : 8000。
我不知道在给土星增加一个音差以使土星的极距离可以构成一个大全音8 : 9的原因当中,它是否应当算一个,抑或它是从运动的前述原因中直接导出的。因此,至于为什么在前面第四章中,土星的音程被发现包含了大约一个大全音,你在这里有的不是一个推论,而是一个原因。
39.命题。土星的精确近日运动以及木星的精确远日运动都不能构成大调的行星的普遍和谐比例。
根据命题31,由于土星的远日运动应当与地球和金星的远日运动构成精确的和谐比例,所以土星的比它的远日运动快4 : 5或一个大三度的运动也将与它们构成和谐比例;因为地球与金星的远日运动构成了一个大六度,而根据第三卷的证明,它又可分解为一个纯四度和一个大三度,因此,土星的这个比已经是和谐的运动还要快(快的量小于一个协和音程)的运动将不会处于精确的和谐。但这样一种运动是土星的近日运动本身,因为根据命题38,土星的近日运动要比远日运动大4 : 5,即一个音差或80 : 81(小于最小的协和音程)。因此,土星的精确近日运动实际上并不和谐。而木星的精确远日运动也并不真正和谐,因为根据命题8,它与土星的近日运动相差一个纯八度,根据第三卷中所说的内容,它也不能处于精确的和谐。
40.命题。根据先验理由建立起来的木星与火星的发散运动的联合和谐比例1 : 8或三个八度必须要加上一个柏拉图小半音[11]。
因为根据命题31,土星与地球的远日运动之间必须构成1 : 32即12 : 384的比例;而根据命题15,地球的远日运动与火星的近日运动之间必须构成3 : 2即384 : 256的比例;根据命题38,土星的远日运动与它的近日运动之间必须构成4 : 5或12 : 15的比例,再加上它的额外增量;最后,根据命题8,土星的近日运动与木星的远日运动之间必须构成1 : 2或15 : 30的比例;因此,在减去土星的额外增量之后,还剩下木星的远日运动与火星近日运动之间的30 : 256。但30 : 256要比32 : 256大30 : 32,即15 : 16或240 : 256,为一个半音。因此,用土星的额外增量(根据命题38,它应当是80 : 81即240 : 243)去除240 : 256,得到的结果是243 : 256。但这是一个柏拉图小半音,约为19 : 20,参见第三卷。因此,1 : 8必须加上一个柏拉图小半音。
于是,木星与火星的较大比例,即发散运动之间的比例应当是243 : 2048,大约是243 : 2187和243 : 1944的平均,即1 : 9和1 : 8的平均。在1 : 9和1 : 8这两个比例中,前面所说的类比要求前者,[12]而和谐比例接近于后者。
41.命题。火星运动的固有比例必定是和谐比例5 : 6的平方,即25 : 36。
因为根据前一命题,木星与火星的发散运动之比应当是243 : 2048,即729 : 6144;而根据命题8,其收敛运动之比应当是5 : 24,即1280 : 6144,因此,两者的固有比例的复合必定是729 : 1280或72900 : 128000。但是根据命题28,木星自身的固有比例必定是6561 : 8000,即104976 : 12800。因此,如果用它去除两者的复合比例,那么得到的商72900 : 104976即25 : 36就是火星的固有比例,它的平方根是5 : 6。
还可以这样来说明:土星的远日运动与地球的远日运动之比为1 : 32或120 : 3840;土星的远日运动与木星的近日运动之比是1 : 3或120 : 360,再加上它的额外增量;土星的远日运动与火星的远日运动之比是5 : 24或360 : 1728。因此,剩下的1728 : 3849再减去土星与木星的发散运动之比中的那个额外增量,就是火星的远日运动与地球的远日运动之比。而地球的远日运动与火星的近日运动之比是3 : 2即3840 : 2500,因此,火星的远日运动与近日运动之比就是1728 : 2560,即27 : 40或81 : 120,再减去所说的额外增量。但是81 : 120是一个小于80 : 120或2 : 3的音差,因此,如果从一个音差里除去2 : 3,再除去所说的额外增量(根据命题38,它等于金星的固有比例),那么剩下来的就是火星的固有比例。而根据命题26,金星的固有比例是一个第西斯减去一个音差。而一个音差加一个第西斯再减去一个音差,就得到一个完整的第西斯或24 : 25。因此,如果用2 : 3即24 : 36减去一个第西斯24 : 25,那么和以前一样,得到的商25 : 36就是火星的固有比例。根据第三章,它的平方根5 : 6就是音程。[13]
这就是在前面第四章中,火星的极距离被发现包含了和谐比例5 : 6的又一个原因。
42.命题。火星与地球之间的较大的共有比例,或者说发散运动的共有比例必定是54 : 125,小于根据先验的理由建立的和谐比例5 : 12。
根据前一命题,火星的固有比例必定是减去了一个第西斯的纯五度;而根据命题15,火星与地球的收敛运动的共有比例,或者说较小的共有比例必定是一个纯五度即2 : 3;最后,根据命题26和28,地球的固有比例必定是减去了一个音差的第西斯的平方。由这些成分复合成了火星与地球之间的较大比例,即它们的发散运动之比;它等于两个纯五度(或4 : 9,即108 : 243)加一个第西斯减去一个音差,即两个纯五度加上243 : 250。也就是说,它等于108 : 250或54 : 125,即608 : 1500。但这个比例要小于625 : 1500即5 : 12,小的量是602 : 625,即约为36 : 37,它小于最小的协和音程。
43.命题。火星的远日运动不可能是任何普遍和谐比例;然而它必定在某种程度上与小音阶保持和谐。
由于木星的近日运动有一个尖声的小调的d音,而且它与火星的远日运动之间必定构成了和谐比例5 : 24,所以火星的远日运动也有一个同样尖的掺杂f音。我之所以说是掺杂的,是因为尽管在第三卷的第十二章,我考察了掺杂的协和音程,并从系统的构成中把它们推了出来,但某些存在于简单自然系统中的掺杂和谐比例被漏掉了。于是,读者们可以在结尾是“81 : 120”的一行后面加上:“如果把它除以4 : 5或32 : 40,那么得到的商27 : 32,一个下小六度[14],即使是在纯粹的八度中,也存在于d与f,或c与e[15],或a与c之间。”在接下来的表中,这句话应当放在第一行:“对于5 : 6,是27 : 32,它是不足的。”
由此很明显,正如根据我的基本原理所规定的,在自然系统中,真正的f音与d音之间构成一个不足的或掺杂的小三度。因此,根据命题13,由于在确立了真正的d音的木星的近日运动与火星的远日运动之间构成了一个纯粹的小三度加两个八度,而不是一个不足的音程,所以火星的远日运动定出的音高要比真正的f音高一个音差。于是,它是一个掺杂的f音;所以它不是绝对地,而是在一定程度上与这个音阶一致。但它不会进入一个普遍的和谐比例,无论是纯的还是掺杂的。因为金星的近日运动占据着这个调音中的e音。但由于e音和f音相邻,它们之间的比例是不和谐。因此,火星与金星的近日运动之间不是和谐的。但它也与金星的其他运动不和谐,因为它们比一个第西斯小一个音差。因此,由于金星的近日运动与水星的远日运动之间是一个半音加一个音差,所以金星的远日运动与火星的远日运动之间将是一个半音加一个第西斯(不考虑八度),即一个小全音,它仍然是一个不协和音程。现在,火星的远日运动与小音阶是一致的,但与大音阶不一致。因为金星的远日运动是大调的e音,而火星的远日运动(不考虑八度)比e音高一个小全音,所以在这个调音中,火星的远日运动必然落在f音和升f音中间,它将与g音(在这个调音中由地球的远日运动所占据)构成不协和的25 : 27,即一个大全音减去一个第西斯。
同样可以证明,火星的远日运动与地球的运动之间是不和谐的。因为它与金星的近日运动之间构成一个半音加一个音差,即14 : 15(根据以前所说的),而根据命题27,地球与金星的近日运动之间构成了一个小六度,即5 : 8或15 : 24。因此,火星的远日运动与地球的近日运动(加上几个八度)之间将构成14 : 24或7 : 12的不和谐比例,它们是不协和音程,7 : 6也是一样。因为5 : 6与8 : 9之间的任何音程都是不协和音程和不和谐比例,比如这里的6 : 7。但地球没有任何一种运动可以与火星的远日运动构成和谐比例。因为前面已经说过,它与地球的远日运动之间构成了不和谐比例25 : 27(不考虑八度),但是从6 : 7或24 : 28到25 : 27之间的所有音程都小于最小的协和音程。
44.推论。因此,从以上关于木星和火星的命题43、关于土星和木星的命题39、关于木星和地球的命题36,以及关于土星的命题32中,我们可以很清楚地看出,为什么在前面的第五章中,我们发现行星的所有极运动都不是完美地处于一个自然系统或音阶中,而且所有那些处于同一调音系统中的极运动并没有以一种自然方式划分那个系统的音高(loca),也没有产生一种协和音程的纯粹自然的接续。因为单颗行星拥有个别的和谐比例、所有行星拥有普遍和谐比例,以及普遍和谐比例有大调和小调两种类型的原因是优先的;当所有这些被假定之后,那么对自然系统所做的各种形式的调整就不再可能了。但是,如果那些原因并不必然是优先的,那么无疑地,或者一个系统和它的一个调音会包含所有行星的极运动;或者如果大调和小调两种调式的歌曲需要两个系统,那么自然音阶的实际秩序既可以在一个大调的系统中表达,也可以在另一个小调的系统中表达。于是,你在这里看到了第五章中对非常小的不一致(它们小于一切协和音程[16])所许诺的理由。
45.命题。金星与水星的较大共有比例,即两个八度,以及在命题12和命题16中根据先验的理由所确立的水星的固有和谐比例,必须加上一个等于金星音程的音程,以使水星的固有比例成为完美的5 : 12,于是水星的两种运动都可以与金星的近日运动构成和谐。
第一,由于土星这个外接于它的正立体形的、最高的、最外层的行星的远日运动,必定与区分立体形级别的地球的最高的运动即远日运动构成和谐,因此,根据相反的定律,水星这个内切于它的正立体形的、最内层的、距太阳最近的行星的近日运动,必定与地球(它是共同的边界)[17]最低的运动即近日运动构成和谐:根据命题33和命题34,前者指定了和谐比例的大调,后者指定了小调。但是根据命题27,金星的近日运动必须与地球的近日运动构成和谐比例5 : 3,因此水星的近日运动也应当与金星的近日运动处于同一个音阶中。然而,根据命题12,先验的理由决定了金星与水星的发散运动之间的和谐比例是1 : 4,因此,根据这些后验的理由,它必须通过加入金星的整个音程来进行调节。因此,金星的远日运动与水星的近日运动之间不再构成两个纯八度,而是金星的近日运动与水星的近日运动之间构成两个纯八度。但是根据命题15,收敛运动之间的和谐比例3 : 5也是纯音程。因此,如果用3 : 5去除1 : 4,得到的5 : 12就是水星的固有比例,它也是纯音程,不过不会(根据命题16,通过先验的理由)再被金星的固有比例所减少。
第二,正如只有外面的土星和木星才不被正十二面体和正二十面体这对配偶立体形接触,也只有里面的水星才不被这对立体形接触,因为它们接触了里面的火星、外面的金星以及处于中间的地球。因此,由于某个等于金星固有比例的比例已经被加给了被立方体和四面体所支撑的土星和木星的运动的固有比例,所以包含在与立方体和四面体有亲缘关系的八面体之内的水星的固有比例也应当加上同样大的值。这是因为,八面体是次级形体中唯一扮演着立方体和四面体这两个初级形体(关于这些,参见第一章)的角色的立体形,所以在内行星中也只有水星扮演着土星和木星这两颗外行星的角色。
第三,因为根据命题31,最高的行星土星的远日运动必定与改变了和谐比例种类的两颗行星中较高的、与之较近的行星的远日运动之间构成若干个八度,即连续双倍比例1 : 32;所以反过来也是这样,最低的行星水星的近日运动也必定要与改变了和谐比例种类的两颗行星中较低的、与之较近的行星的近日运动之间构成若干个八度,即连续双倍比例1 : 4。
第四,只有土星、木星和火星这三颗外行星的极运动可以构成普遍和谐比例,所以内行星水星的两种极运动也必定可以构成同样的和谐比例,而根据命题33和命题34,中间的行星地球和金星必定会改变和谐比例的种类。
第五,在三对外行星中,它们的收敛运动之间存在着完美的和谐比例,但发散运动之间以及单颗行星的固有比例之间则存在着经过调节的(fermentatae)和谐比例;因此,反过来也是这样,在两对内行星中,完美的和谐比例主要不应在收敛运动之间发现,也不应在发散运动之间发现,而应在同侧的运动[18]之间发现。由于两种完美的和谐比例应当属于地球和金星,所以金星和水星也应当具有两种完美的和谐比例。地球和金星的远日运动之间以及它们的近日运动之间都应当被分配一个完美的和谐比例,因为它们必定改变了和谐比例的种类;而金星和水星由于没有改变和谐比例的种类,所以也不要求在远日运动之间和近日运动之间构成完美的和谐比例。然而,与远日运动之间的经过调节的完美和谐比例不同,收敛运动之间却存在着完美的和谐比例。正如内行星中最高的行星金星的固有比例是所有行星中最小的(根据命题26),内行星中的最低的行星水星的固有比例是所有行星中最大的一样(根据命题30),所以金星的固有比例也是所有行星的固有比例中最不完美的,或是与和谐比例相距最远的,而水星的固有比例也是所有行星的固有比例中最完美的,也就是说绝对和谐的、没有经过任何调节的比例;最终,这些关系在任何方面都是相反的。
超越一切时代的永恒的他就这样装点了他伟大的智慧杰作:没有多余,没有瑕疵,没有任何可指摘之处。他的作品是何等令人渴慕啊!所有事物都是一方平衡着另一方,没有任何东西是缺少对方而存在的。他为每一样东西都建立了善(装饰和匀称),并以最好的理由确证了它们,谁会对它们的光辉感到饱足呢?
46.公理。立体形在行星天球之间的镶嵌如果不受约束,不被前面所说的原因的必然性所限,那么它就应当完全遵循几何内切与外接的比例,于是也要遵循内切球与外接球之比的条件。[19]
物理镶嵌能够精确地表现几何镶嵌,就像一件印刷作品精确地表现它的纹样一样,没有什么东西能比这更合理、更适当了。
47.命题。如果行星之间的正立体形的镶嵌不受限制,那么四面体的顶点就必定会触到上方的木星的近日天球,其各面的中心会触到下方的火星的远日天球。然而,顶点分别位于各自行星的近日天球上的立方体和八面体,它们各面的中心必定穿过了它们内部的行星天球,以至于那些中心将会位于远日天球与近日天球之间;而顶点接触外面行星的近日天球的十二面体和二十面体,它们各面的中心必定不会达到它们内部的行星的远日天球;最后,顶点位于火星近日天球的十二面体的“海胆”的反转的边[20](连接着它的两个立体角或“楔子”)的中点 ,必定非常接近金星的远日天球。
由于无论是从起源上说,还是从在世界中的位置上说,四面体都是初级形体中的中间一个,所以如果不受阻碍,它必定会相等地跨过木星和火星两个区域。因为立方体在它之上,也在它之外,二十面体在它之下,也在它之内,所以很自然地,它们的镶嵌会带来相反的结果(四面体介于二者之间),即其中一个立体形的镶嵌是盈余的,另一个立体形的镶嵌是亏缺的,这就是说一个会穿过内部行星的天球,另一个则不会穿过。由于八面体与立方体同源,它的两球之比与立方体相等,二十面体与十二面体同源,因此,如果立方体的镶嵌存在着某种完美性,那么同样的完美性也必定属于八面体;如果十二面体的镶嵌存在着某种完美性,那么同样的完美性也必定属于二十面体。八面体的地位也非常类似于立方体的地位,二十面体的地位也非常类似于十二面体的地位,因为正如立方体构成了通往外部世界的一个界限,八面体也构成了通往内部世界的一个界限,而十二面体和二十面体则处于中间。因此很自然地,它们的镶嵌方式也将是类似的,前者的情况是穿过了内部行星的天球,后者的情况则是没有达到内部行星的天球。
然而,用角的顶点来表示二十面体和用底来表示十二面体的“海胆”,却必定会充满、包含或安排两个区域,即属于十二面体的火星和地球之间的区域以及属于二十面体的地球和金星之间的区域。但哪对行星应该属于哪种关系,前一公理已经说得很清楚了。根据本卷第一章,拥有一个有理的内切球的四面体被分配到了初级形体的中间位置,它的两边都是不可公度的球形的立体形,外面的是立方体,里面的是十二面体。这种几何性质,即内切球的有理性,从本质上代表了行星天球的完美镶嵌。而立方体和它的共轭立体形的内切球只有平方之后才是有理的,因此,它们代表一种半完美的镶嵌,在这种镶嵌中,尽管行星天球的尽头没有被立体形各面的中心所触及,但至少它的内部,即远日天球和近日天球之间的平均——如果因其他理由这是可能的话——却被各个中心所触及。而另一方面,十二面体和它的共轭立体形的内切球无论是半径的长度,还是半径长度的平方,都是无理的;因此,它们代表着一种绝对非完美的镶嵌,不与行星天球的任何地方相接触,即各面中心无法达到行星的远日天球。
尽管“海胆”与十二面体及其共轭立体形同源,但它与四面体有某种类似之处。因为内切于它的反转的边的球[21]的半径与外接球的半径不可公度,但却与两临角之间的距离可公度[22]。于是,半径的可公度性的完美性几乎与四面体一样大,而它的不完美性却与十二面体及其共轭立体形一样大。因此,很自然地,属于它的物理镶嵌既不是绝对的四面体式的,也不是绝对的十二面体式的,而是一个居间的种类。因为四面体的各面必定会触及天球的外表面[23],十二面体的各面与之还相差一定距离,所以这个楔状立体形用其反转的边处于二十面体的空间和内切球的外表面之间,并且几乎触及这个外表面——如果这个立体形能够与其余五种立体形保持一致,如果它的定律也许能被其余五种立体形的定律所准许。然而,为什么我要说“也许能被准许”?没有这些定律,它们就不可用。因为如果一种松散的、不接触的镶嵌与十二面体相合,那么除了这个与十二面体和二十面体同源的辅助立体形——这个立体形的镶嵌几乎可与它的内切球接触,而且与天球的距离(如果的确存在这段距离的话)不会大于四面体超过和穿过[天球]的量——之外,还有什么能把那种无限制的松散局限在一定范围之内呢?我们在下面就会讨论到这个量。
“海胆”之所以会与两个同源立体形结合(也就是说,为了能够确定它们留下来的尚未确定的火星与金星的天球之比),很可能是因为这一事实:地球的天球半径1000非常接近于火星的近日天球和金星的远日天球的比例中项,就好像“海胆”指派给与它同源的立体形的空间已经在它们之间被成比例地分开了一样。
48.命题。正立体形在行星天球之间的镶嵌不是纯粹自由的,因为它在每一个细节处都被极运动之间建立起来的和谐比例所阻碍了。
根据公理1和公理2,每一个立体形的两球之比不是直接由立体形本身所表达的,而是通过立体形,首先找到与天球的实际比例最接近的和谐比例,然后把它调整到极运动。
其次,根据公理18和公理20,为了使两种类型的普遍和谐比例能够存在,每一对行星的较大和谐比例必须要根据后验的理由进行调节。因此,根据第三章中所阐明的运动定律,为了使这些理由可以成立,可以通过它们自己的理由而得到支持,[由和谐比例建立起来的]距离与从两球之间的立体形的完美镶嵌中得到的距离就应该有些出入。为了证明这一点,并且弄清楚每一颗行星有多少距离被通过恰当理由建立起来的和谐比例带走了,让我们通过一种以前从未有人尝试过的新的计算方法来从和谐比例中导出行星与太阳之间的距离。
这项探索分为三步:第一,由每颗行星的两种极运动导出行星与太阳之间的极距离,通过它们计算出由每颗行星所固有的极距离来确定的轨道半径;第二,从以同样单位量出的同样的极运动中导出平均运动和它们之间的比例;第三,通过已经揭示出来的平均运动之比,求出轨道之比或平均距离之比以及极距离之比,再把它与从立体形中导出的比例进行比较。
关于第一步,我们必须回忆一下第三章第六条的内容,即极运动之比等于行星与太阳的相应极距离之比的倒数的平方。因此,由于平方之比是比的平方,所以单颗行星的极运动的数值将被当作平方数,它的根将给出极距离的大小。要想求出轨道半径和偏心率,只要取它们的算术平均值就可以了。于是,至此建立起来的和谐比例就规定了:
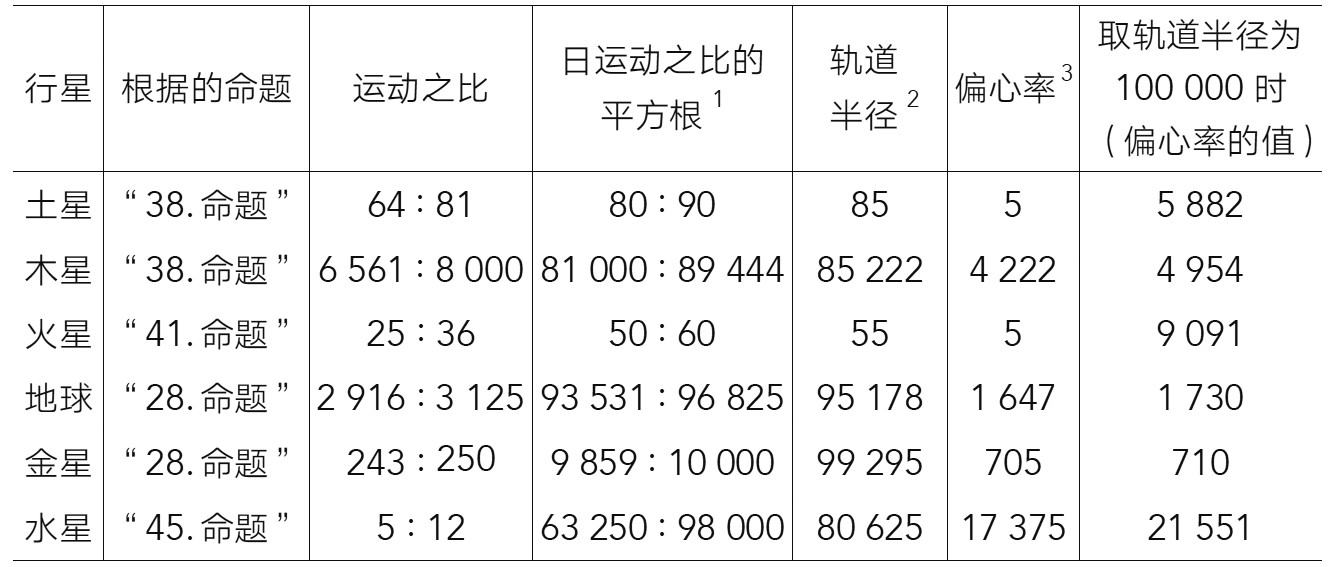
1.这里的比例有的乘上了共同因子,有的取了随意的精度。
2.极距离的平均值。每个值的单位都是各自行星极距离的单位。
3.半径与任一极距离之差。每个值的单位都是各自行星极距离的单位。
关于第二步,我们又一次需要借助第三章的第十二条,即平均运动既小于极运动的算术平均值,也小于其几何平均值,然而它小于几何平均值的量却等于几何平均值小于算术平均值的量的一半。由于我们所要求的是用同样单位来表示的所有平均运动,所以让我们把迄今为止在两种运动之间建立起来的所有比例以及单颗行星的所有固有比例都按照它们的最小公因子确立起来,然后再取每颗行星的极运动之差的一半为算术平均值,取两极距离之积与这个积的平方根之差为几何平均值,再从几何平均值中减去算术平均值与几何平均值之差的一半,我们便得到了以每颗行星极运动的固有单位建立起来的每颗行星的平均运动的数值,根据比例规则,它们可以很容易地转化成公共单位的值。
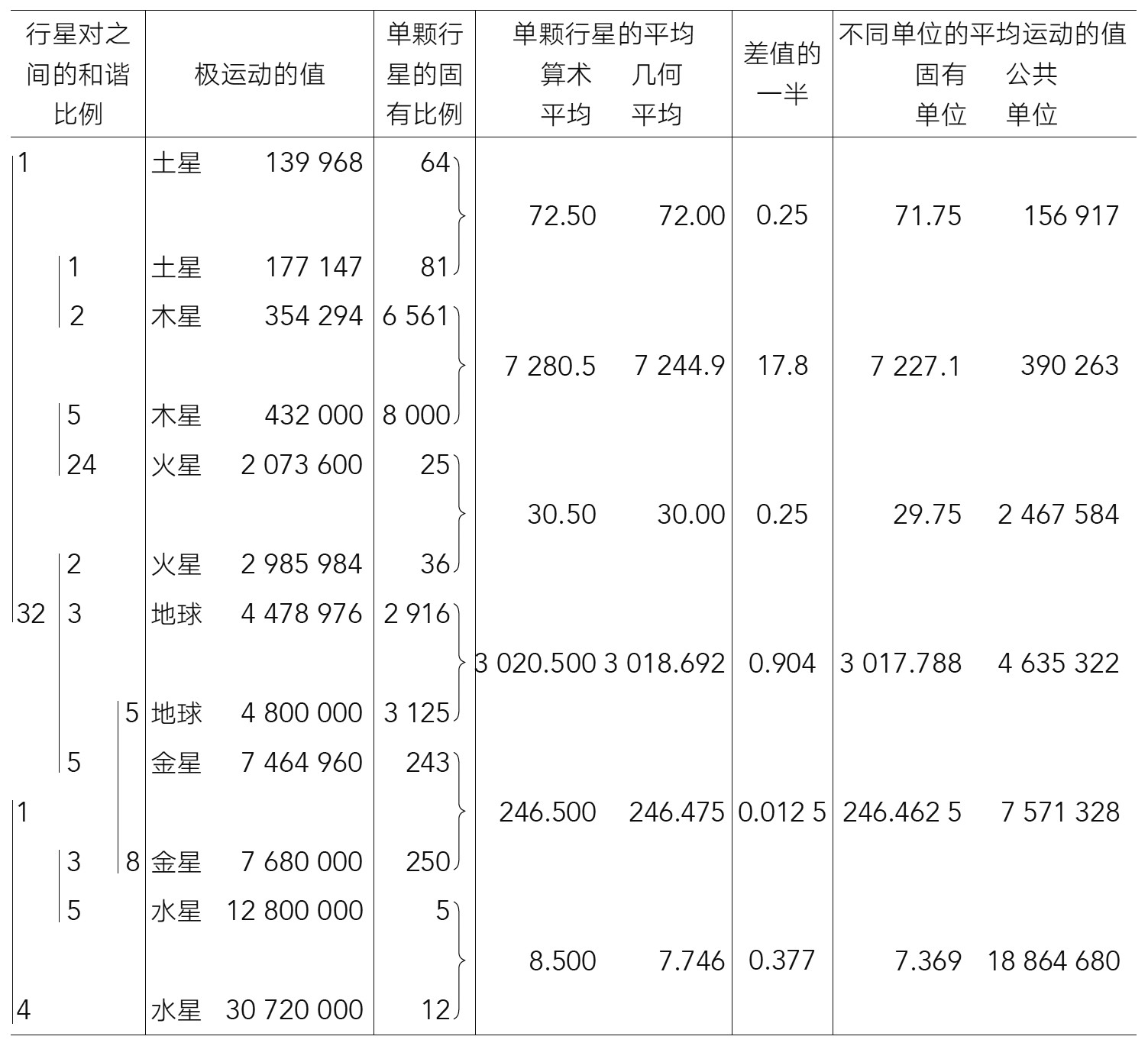
于是,我们就从规定的和谐比例得到了平均周日运动之比,即每两颗行星的度数和分数之比。很容易检验它们是多么接近天文学。
第三步则需要第三章的第八条。在求出了单颗行星的平均周日运动之比以后,我们也可以求出它们的轨道之比。因为平均运动之比等于轨道反比的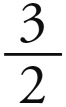 次方,而立方之比就是克拉维乌斯(Clavius)在其《实用几何学》(Practical Geometry)一书的附表中所给出的那些平方之比的
次方,而立方之比就是克拉维乌斯(Clavius)在其《实用几何学》(Practical Geometry)一书的附表中所给出的那些平方之比的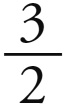 次方。[24]因此,如果我们的平均运动的值(如果需要,可以简化成同样的位数)需要在那个表的立方值中去寻找,那么它们会在它们左边的平方数一栏中指示出轨道之比的值。于是,前面被归于单颗行星的以行星的轨道半径为单位的偏心率,就可以很容易地通过比例规则被转化成对所有行星都适用的公共单位下的值。然后,通过把它们加到轨道半径上和从轨道半径中减去它们,行星与太阳之间的极距离就可以确定了。不过,根据天文学的惯常做法,我们将把地球的轨道半径定为100 000,以使这个数无论平方还是立方,都仅由零组成。我们也可以把地球的平均运动提高到10 000 000 000,并通过比例规则,使得任一行星的平均运动的数值与地球的平均运动之比,等于10 000 000 000比上这个新的值。因此,这项工作可以通过分别把五个立方根与地球的值进行比较来进行。
次方。[24]因此,如果我们的平均运动的值(如果需要,可以简化成同样的位数)需要在那个表的立方值中去寻找,那么它们会在它们左边的平方数一栏中指示出轨道之比的值。于是,前面被归于单颗行星的以行星的轨道半径为单位的偏心率,就可以很容易地通过比例规则被转化成对所有行星都适用的公共单位下的值。然后,通过把它们加到轨道半径上和从轨道半径中减去它们,行星与太阳之间的极距离就可以确定了。不过,根据天文学的惯常做法,我们将把地球的轨道半径定为100 000,以使这个数无论平方还是立方,都仅由零组成。我们也可以把地球的平均运动提高到10 000 000 000,并通过比例规则,使得任一行星的平均运动的数值与地球的平均运动之比,等于10 000 000 000比上这个新的值。因此,这项工作可以通过分别把五个立方根与地球的值进行比较来进行。
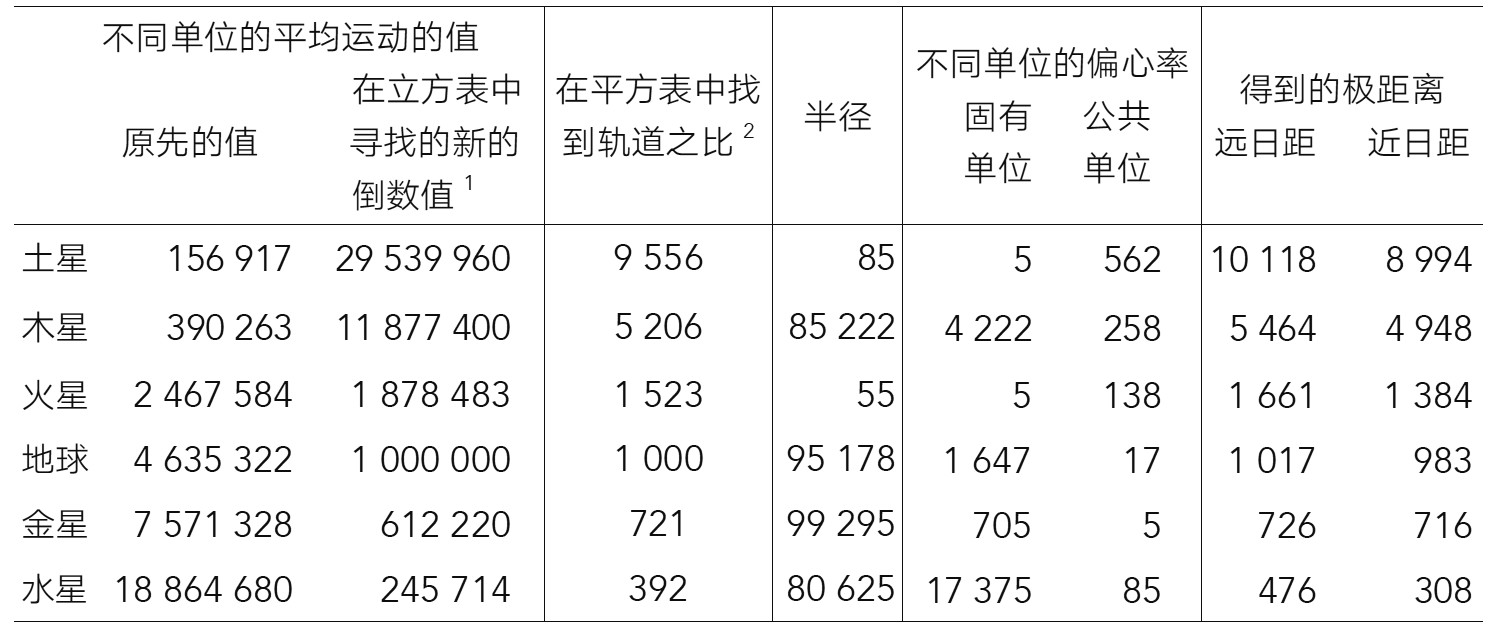
1.这一列的值是用地球的平均运动4 635 322除以前一列的值,再乘以1 000 000得到的。
2.这一列的值是把前一列的值的立方根平方,再除以10得到的。
因此,我们在最后一列就可以看出两颗行星的收敛距离应该是多少了。所有的值都非常接近我在第谷的观测数据中发现的那些距离[25],只有水星有一些小的出入。天文学给它的距离似乎是470,388和306,这些值都偏小。我们也许可以合理地猜想,这里的不一致的原因或者是因为观测次数太少,或者是因为偏心率太大。(参见第三章)不过我还是快点把计算完成吧!
现在就很容易把立体形的两球之比与收敛距离之比进行比较了(见下表)。
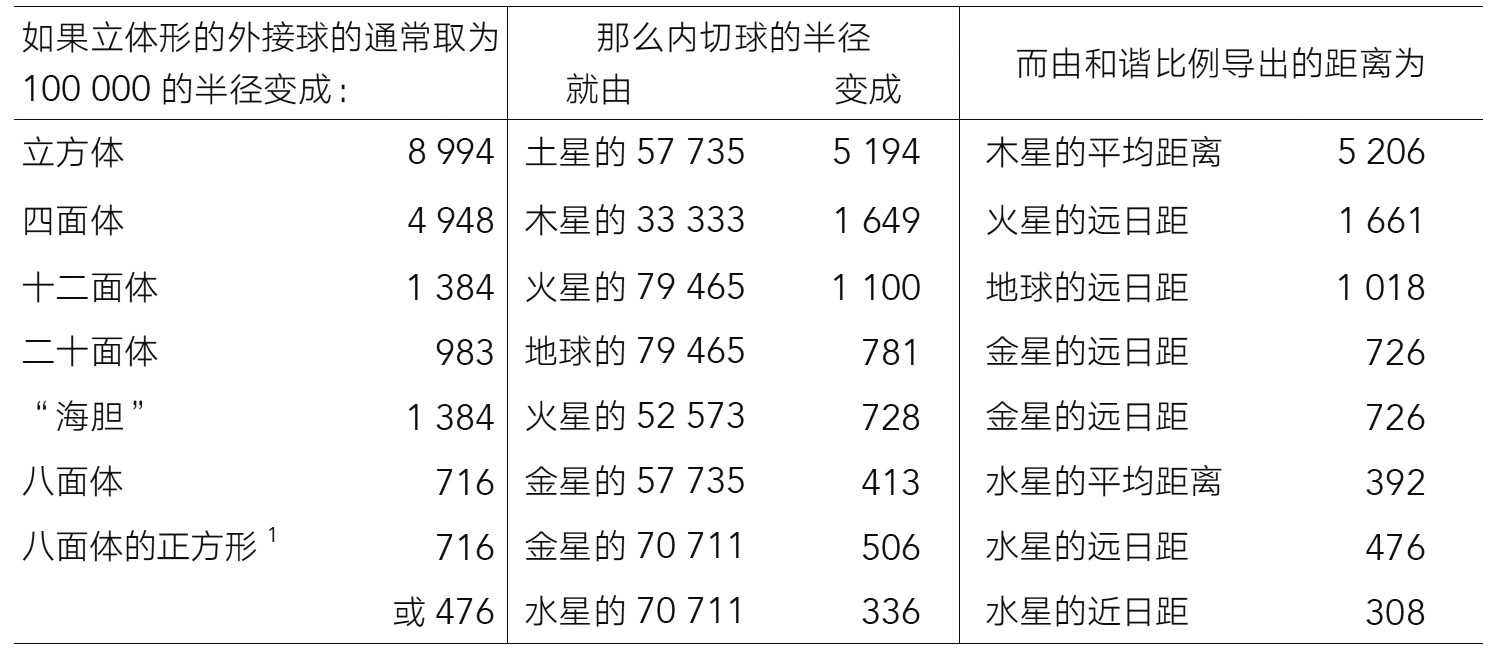
1.开普勒试图(但未获成功)在这个表的最后两行使用“八面体的正方形”(正八面体腰部的四个点所连成的正方形)的比例。开普勒曾在《宇宙的奥秘》第13章中说,水星的远日轨道也许是内切于这个正方形内,而不是内切于八面体内,因为他发现,用八面体的正方形中的圆代替内切球作为水星轨道的外边界是更合适的。他在这里表明,八面体正方形的过小的比例不能与金星的近日天球和水星的远日天球很好地符合,也不能与水星的近日天球和远日天球符合。他完全愿意抛弃年轻时的想法。正如他在之前说的:“平面图形能在立体中起什么作用呢?”
也就是说,立方体的面向下稍微伸进了木星的中圆;八面体的面还没有达到水星的中圆;四面体的面稍微伸进了火星的远日圆;“海胆”的边还没有达到火星的远日圆;但十二面体的面远远不到地球的远日圆;二十面体的面也几乎同样程度地没有达到金星的远日圆;最后,八面体的正方形一点都不相配,不过这没有什么坏处,平面图形能在立体中起什么作用呢?因此,你看到,如果行星距离是从迄今证明的运动的和谐比例中导出的,那么前者的大小必定会像后者所允许的那样大,但不像由命题45所规定的自由镶嵌定律所要求的那样大。这是因为,借用本卷卷首的盖伦的话来说,这种完美镶嵌的“几何装点”与其他可能的“和谐装点”并非完全一致。为了澄清这一命题,许多东西都必须通过实际的数值计算来证明。
我并不隐瞒这一事实:如果我通过金星运动的固有比例来增加金星与水星的发散运动的和谐比例,并因而把水星的固有比例减少同样的量,那么这样一来,我就得到了水星与太阳之间的如下距离——469,388,307,它们与天文学给出的值精确相符。但是首先,我不能用和谐理由来保证这种减少,因为水星的远日运动将不会与任何音阶相符,而且在那些相互对立的行星中,完整的对立模式也没有在一切方面被保留下来;其次,水星的平均周日运动过大,以至于整个天文学中最为确定的水星周期被太大地缩短了。但通过这个例子,我鼓励所有那些有机会读到这本书,并且一心致力于数学的原理和最高哲学的知识的人们:努力工作,或者抛弃在任何地方都适用的和谐比例中的一种,把它换成另一种,看看你是否可以接近第四章所提出的天文学;或者用理性去论证,你是否可以用天体运动建立某种更好的、更适当的东西,它可以或者部分或者全部地摧毁我已经使用过的方案。无论属于我们造物主的荣耀的有哪些东西,它们都可以经由本书平等地为你所使用。直到这一刻,我认为自己完全可以改变任何我发现早先想得不正确的东西,它们往往是一时不留意或心血来潮的产物。
49.总结。在距离创生的时候,立体形让位于和谐比例,行星对的较大和谐比例让位于所有行星的普遍和谐比例(直至后者成为必然的),这是恰当的。
蒙天恩眷顾,我们现在碰到了49,即7的平方;这也许就像一种安息日,紧接着前面关于天的构造的六次八个一组的讨论。而且,尽管它本可以放在早先的公理中说,但我还是很恰当地把它写成了总结:因为上帝在欣赏他的创世工作时也是这样做的,“神看着一切所造的都甚好”。[26]
这篇总结分为两部分:首先是一则关于和谐比例的一般性的证明,它是这样的:只要是在分量不等的不同东西中进行选择,那么首先应该选的就是更优秀的东西,而且只要可能,更拙劣的东西就应该让位于它,就像“装点”一词似乎表明的那样。正如生命比物体更优秀,形式比质料更优秀一样,和谐装点也比几何装点更优秀。
正如生命完善了生命体,后者天生就是用来实现生命功能的一样(因为生命是从作为神的本质的世界原型中来的),[27]运动也度量了被指派给每颗行星的区域,因为一块区域被指派给行星,就是为了使它能够运动的。但是五种正立体形,根据它们的名字本身,与区域的空间、数目和物体有关,而和谐比例却与运动有关。再有,由于质料是弥散的、本身不明确的,而形式是明确的、统一的、能够确定质料的,所以虽然存在着无限数量的几何比例,但只有极少数才是和谐比例。因为尽管在几何比例中存在着确定、形成和限制的程度,而且通过把天球归于正立体形,只有三个比例可以形成;但即使是这些几何比例,也被赋予了一种为其余所共有的偶性,即预设了一种对量的无限种可能的分割,那些各项彼此不可公度的比例实际上也以某种方式包含了这种性质。但和谐比例都是有理的,它们所有的项都是可公度的,都是得自于确定而有限的平面图形种类。无限可分性意味着质料,而项的可公度性或有理性却意味着形式。因此,正如质料渴望形式,一块适当大小的粗凿的石头渴望人体的形状一样,形体的几何比例也渴望和谐比例——不是为了后者能够塑造和形成前者,而是为了某种质料能与某种形式符合得更好,石头的尺寸与某个雕塑符合得更好,形体的比例与和谐比例符合得更好;从而使它们能够被塑造和形成得更完善,质料被它的形式所完善,石头被凿子凿成一个生命体的样子,而立体形的球的比例通过它最接近的、适当的和谐比例来形成。
我们迄今所说的东西可以通过我的发现史而变得更清楚。当我在24年前沉浸在这种沉思中时,我首先研究了单颗行星的天球是否彼此等距(因为在哥白尼那里,天球是分离的,而不是彼此接触的)。当然,我认为没有什么能比相等的关系更美妙了。然而,这种关系没头没尾,因为这种质料上的相等没有给出运动星体的数目,也没有给出确定的距离。于是,我开始思考距离与天球的相似性,即它们的比例。但同样的麻烦出现了,因为尽管这时天球之间的距离是不等的,但它们并不像哥白尼所认为的那样是不均匀地不等的,而且也没有给出比例的大小和天球的数目。于是,我继而考虑正平面图形:它们通过圆的归属而产生了距离,但仍没有给出确定的数值。最后,我想到了五种正立体:这时,无论是星体的数目还是距离的几乎正确的数值都被揭示了,以至于我把余下的不一致归于天文学的精确程度。天文学的精确性在这20年里被完善了许多;[但是]注意!在距离与正立体形之间仍然存在着出入,而且偏心率在行星中的分布相当不均等的原因也没有得到揭示。在这个世界的居巢中,我一直都只是在寻找石头——虽然可能是一种更优雅的形状,但终归是适合于石头的——而没有意识到雕刻家已经把它们塑造成了一尊非常考究的有生命的雕像。于是渐渐地,特别是在过去的这三年里,我想到了和谐比例,而把正立体形弃做较不重要的东西。这既是因为和谐比例是基于最后一触所给予的形式,而正立体形却基于质料(它在宇宙中只是星体的数目和距离的大致距离),也是因为和谐比例能够给出偏心率,而立体形却丝毫不能保证。也就是说,和谐比例提供了雕像的鼻子、眼睛和其余部分,而立体形却只是规定了粗略的外在大小。
因此,正如生命体和石块都不是根据某种几何形体的纯规则制成的,而是有某种东西从外在的球形中去除,无论它可能有多么精妙(尽管体积的正确大小保持不变),于是身体能够得到为生命所必需的器官,石头能够得到生命体的形象;所以正立体形为行星天球规定的比例是低等的,它只关注身体和质料,因而必须尽一切可能让位于和谐比例,以使和谐比例更能为天球的运动增辉。
结尾的另一个部分是关于普遍和谐比例的,它也有一个证明,这个证明是与前一个证明紧密相关的。(事实上,它在前面公理18中就已经被部分地假设了。)完美的最后一触属于那种使世界更完美的东西,而那种较为次要的东西要被去除(如果有一方要被去除的话)。然而,使世界更为完美的是所有行星的普遍和谐比例,而不是相邻两颗行星的两个和谐比例。因为和谐比例是单位的某种关系,所以如果所有行星都能统一于同一个和谐比例,而不是每两颗行星分别形成两个和谐比例,那么行星就更加统一了。因此,两颗行星所产生的两个和谐比例中必有一个需要屈从,以使所有行星的普遍和谐比例能够成立。然而,需要屈从的比例必须是发散运动的较大和谐比例,而不是收敛运动的较小和谐比例。因为如果发散运动发散了,那么它们所关注的就不再是这一对行星,而是其他相邻的行星了;而如果收敛运动是收敛的,那么一颗行星的运动就会关注另一颗行星的运动:例如,在木星和火星这对行星中,木星的远日运动会关注土星的运动,火星的近日运动会关注地球的运动;而木星的近日运动会关注火星的运动,火星的远日运动会关注木星的运动。因此,收敛运动的和谐比例对于木星和火星是更适合的,而发散运动的和谐比例对于木星和火星来说就比较远了。如果与两颗相临行星离得较远的、较为不一致和谐比例能够被调整,而不是它们的固有比例,即相临行星的更加相临的运动之间存在的比例被调整,那么把临近的行星两两组合到一起的和谐比例就较少受到破坏。然而,这种调整不会很大。因为比例关系已经被找到了,由此既可以建立所有行星的普遍和谐比例(两种不同种类),又可以包容两颗临近行星的个别的和谐比例(幅度仅为一个音差):事实上,四对收敛运动的和谐比例是纯的,一对远日运动和两对近日运动的和谐比例也是纯的;然而,四对发散运动的和谐比例却相差不到一个第西斯(使华丽音乐中的人声几乎总是走调的最小音程);而只有木星和火星的这种差距在一个第西斯和一个半音之间。因此,这种相互屈从在任何地方都是非常好的。
至此,这篇关于造物主的作品的结尾就完成了。最后,我要把我的目光从证明表上移开,把双手举向天空,虔诚而谦卑地向光芒之父祈祷:
噢,您通过自然之光在我们心中唤起了对恩典之光的渴望,由此将荣耀的光芒洒向我们;创造我们的上帝啊,我感谢您,您使我醉心于您亲手创制的杰作,令我无限欣喜,心神荡漾。看,我已用您赋予我的全部能力完成了我被指派的任务;我已尽我浅薄的心智所能把握无限的能力,向阅读这些证明的人展示了您作品的荣耀。我的心智已经为最完美的哲学做好了准备。如果我这只在罪恶的泥淖中出生和长大的卑微的小虫提出了任何配不上您的意图的东西,那么请启示我理解您的真正意图,并对它们加以改正;如果我因您的作品的令人惊叹的美而不禁显得轻率鲁莽,或者在这样一部旨在赞美您的荣耀的作品中追求了我自己在众人中的名,那么请仁慈地宽恕我;最后,愿您屈尊使我的这些证明能够为您的荣光以及灵魂的拯救尽一份绵薄之力,而千万不要成为它们的障碍。
[1]要想让收敛运动表示一个小音程,行星之间必须非常接近。然而,五种正立体在行星球之间的嵌入给相邻两颗行星的距离设置了下限。对于正二十面体和正十二面体来说,它们的外接球与内切球的半径之比是最小的,即约为1000 : 795。开普勒认为,这个比例对于让收敛运动产生一个大三度或小三度是太大了。
[2]这里的1 : 2和1 : 3是第一卷中所说的“初级立体形家族中的首领”。第一家族包括边数为2,4,8……的立体形(或准立体形),第二家族包括边数为3,6,12……的立体形。参见第一卷,命题30。
[3]当开普勒在行星球之间镶嵌正多面体时,他是从最高的行星开始的。开普勒解释说,由于恒星区域是宇宙中最重要的部分,所以立方体作为初级形体中的第一种,理应离恒星天球最近,从而确定了第一个距离比例,即土星与木星的距离之比。行星的自然顺序也就可以由此确定下来了。开普勒需要下一个命题来确定哪一颗行星应当拥有大三度和小三度。
[4]“较小”和“较大”的和谐比例等价于我们现在所说的“相距更近”和“相距更远”的和谐比例。——Elliott Carter, Jr.
[5]收敛运动之比小于1 : (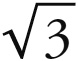 )
)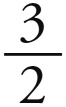 =1 : 2.28。因此1 : 3大于收敛运动之比,1 : 4也太大。1 : 3比收敛运动的真正比例大出3 : 3.28=1.32 : 1,1 : 4比收敛运动的真正比例大出4 : 3.28=1.75 : 1=1.32² : 1。
=1 : 2.28。因此1 : 3大于收敛运动之比,1 : 4也太大。1 : 3比收敛运动的真正比例大出3 : 3.28=1.32 : 1,1 : 4比收敛运动的真正比例大出4 : 3.28=1.75 : 1=1.32² : 1。
[6]火星与地球的发散运动之比是5 : 12,即一个八度加小三度,收敛运动之比是2 : 3,即一个纯五度。这是不搭配的,因为2 : 3并没有改变和谐比例的种类。
[7]地球与金星是唯一一对远日运动和近日运动之间,而不是收敛运动和发散运动之间构成和谐比例的行星。其远日运动的比例是0.602(大六度=0.600),近日运动的比例是0.628(小六度=0.625)。
[8]“同音和谐比例”是指像3 : 5,3 : 10,3 : 20……这样的比例。——原注
[9]关于对小于协和音程的音程的划分,开普勒使用了音差而没有任意进行划分,是因为他在命题26中说,即使和谐的本性没有对这种音程的划分提供更有分量的理由,上帝也不会没有任何缘由地规定一个东西。
[10]参见脚注“音程与和谐比例的比较”。——原注
[11]《蒂迈欧篇》,36。——原注
[12]参见命题13。
[13]根据第三章第六条,偏心圆上的视周日弧之比几乎精确地等于它们与太阳之间的距离的反比的平方。
[14]这里“六度”(sexta)可能应当是“三度”(tertia)。—— Elliott Carter, Jr.
[15]C和e在“自然系统”中并不产生一个下小三度。—— Elliott Carter, Jr.
[16]也就是小于一个第西斯。
[17]第一章中区分了正立体形的雌雄等级。雄雄立体形连同雌性同体的正四面体位于地球以上,雌性立体形则位于地球以下,因此地球的轨道就成为一个边界。
[18]近日运动或远日运动。
[19]这条公理强调了正多面体在确定行星距离方面所起的作用,它使得开普勒能够把严格的镶嵌与观察到的距离之间所可能产生的不一致,解释成在构造宇宙过程中占据优先地位的和谐比例的必然结果。
[20]“反转的边”是指构成“海胆”核的正十二面体的边。
[21]通过构成“海胆”核的十二面体的各边中点的球。
[22]内切于反转的边的球的半径等于两临角间距的一半。
[23]天球必定接触到了四面体各面的中心。
[24]C. Clavius, Geometriae Practicae (Rome, 1604)。开普勒大约在1606年10月得到了这本书。在第8卷末尾,克拉维乌斯列了一张从1到1000的平方和立方表。
[25]从第谷的观测数据中导出的距离已经在第四章中给出。
[26]《创世记》1:31。
[27]参见第四卷。
