电气设备的实际电路几乎都不是单一的电阻、电感或电容电路。最常见的是电阻与电感串联的电路,如电动机、变压器等。
在电阻、电感串联电路中,各元件上的电压和总电压的关系,如图1-30所示。
在电压u的作用下,通过R、L的电流为i,i与R上的压降uR同相位,i比L上的压降uL落后90°。画相量图时,以电流I·为参考相量,再画出电阻上的电压U·R相量和电感上的电压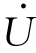 L相量,总电压
L相量,总电压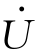 等于
等于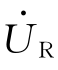 和
和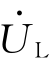 的相量和。从图1-30(b)看出,总电压
的相量和。从图1-30(b)看出,总电压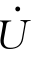 与
与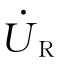 、
、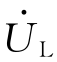 构成了一个直角三角形,称为电压三角形。其斜边为总电压
构成了一个直角三角形,称为电压三角形。其斜边为总电压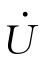 ,两直角边分别为
,两直角边分别为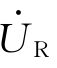 、
、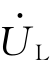 ,根据勾股定律可得
,根据勾股定律可得
![]()
或
![]()
式中 ![]() ——交流电路的阻抗,用Z表示,阻抗的单位也是Ω。
——交流电路的阻抗,用Z表示,阻抗的单位也是Ω。
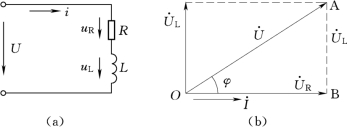
图1-30 电阻和电感串联电路
(a)电路图;(b)相量图
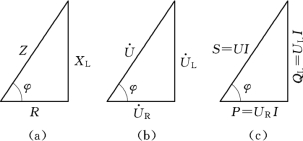
图1-31 阻抗、电压、功率三角形
(a)阻抗三角形;(b)电压三角形;(c)功率三角形
由上式看出,Z、R、XL之间也是一个直角三角形,称为阻抗三角形,如图1-31(a)所示。
从图1-31(b)看出,总电压和电流之间的相位差为φ,即总电压和电流之间的相位差由负荷电阻和感抗的大小决定。
在电阻、电感串联电路中的有功功率也是电阻上消耗的有功功率为
![]()
由电压三角形可知(https://www.daowen.com)
![]()
所以
![]()
式中,cosφ称为电路的功率因数,可由阻抗三角形求得,其数值与负荷的阻抗参数有关。
在电阻、电感串联电路中的无功功率为
![]()
由电压三角形可知
![]()
所以
![]()
在电阻、电感串联电路中的视在功率为
![]()
由视在功率S、有功功率P、无功功率Q组成的三角形,称为功率三角形,如图1-31(c)所示。视在功率为S=![]() 。
。
【例1-9】 有一个电阻R=6Ω,电抗L=25.5mH的线圈,串接于U=220V、50Hz的电源上,试求线圈的感抗XL、阻抗Z、电流I、电阻压降UR、电感压降UL、功率因数cosφ、有功功率P、无功功率Q和视在功率S。
解:由题意有
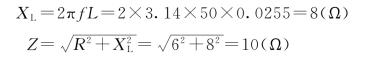
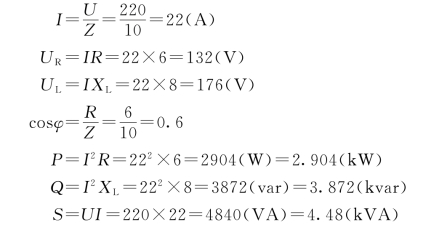
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







