单纯形法的计算公式优化建议：简述单纯形法计算公式

设线性规划

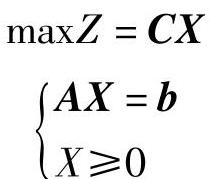
其中A_m×n且r（A）m。

假设A=（P₁，P₂，…，P_n）中前m个列向量构成一个可行基，记为B=（P₁，P₂，…，P_m），后n-m列构成的矩阵记为N=（P_m+1，P_m+2，…，P_n），则A可以写成分块矩阵A=（B，N）。

对于基B，基变量X_B=（x₁，x₂，…，x_m）^T，非基变量X_N=（x_m+1，x_m+2，…，x_n）^T。则X可写为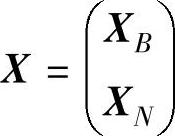。同理，C可写为C=（C_B，C_N），C_B=（c₁，c₂，…，c_m），C_N=（c_m+1，cm+2，…，cn）。因此AX=b可写成：

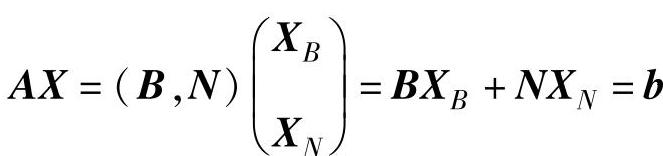
又因r（B）=m，即B≠0，所以存在B^-1，则有：

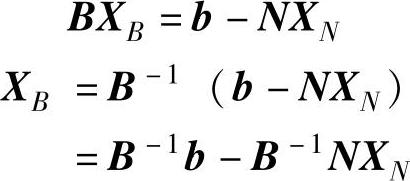
令非基变量X_N=0，则X_B=B^-1b。因此可得到原问题的基本可行解为：

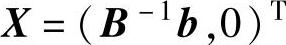
此外，Z=CX可写成：

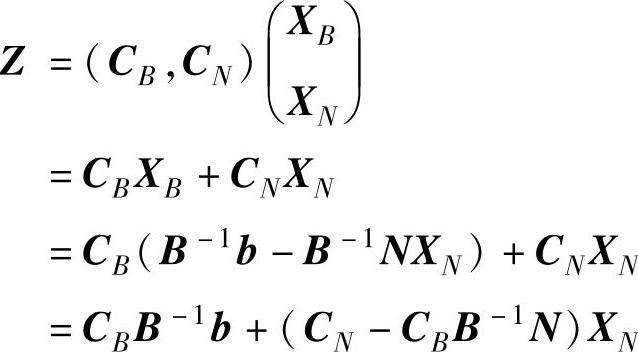
令非基变量X_N=0，Z的值为：

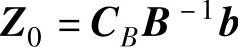
非基变量的检验数λ_N为：

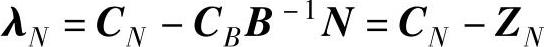
C_BB^-1称为单纯形乘子，记为：

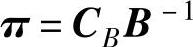
因而当已知线性规划的可行基B时，求得B^-1，根据上述矩阵运算公式就可求得单纯形法所要求的结果。

上述公式可用简单的矩阵表格运算得到，如表1-13所示。

用B^-1左乘表1-13的第二行，将基矩阵B变换为E（m阶单位矩阵），便可得到基本可行解，见表1-14。由表1-13和表1-14的第二行可知B^-1N是N通过初等行变换后的结果，记为N=B^-1N。

将目标函数中基变量的系数C_B变换为零，将表1-14的第二行左乘-C_B后加到第三行，就可求得检验数和目标值，见表1-15。

表1-13

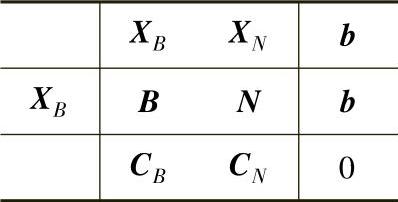
表1-14

(https://www.daowen.com)

表1-15

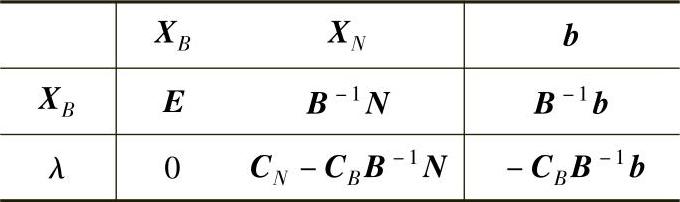
将上述常用公式总结如下：

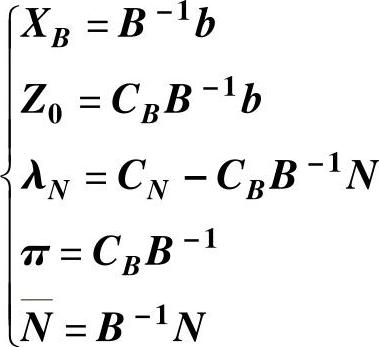
λ_N是n-m个非基变量的检验数，应用λ=C-CB^-1A表示全部变量的检验数。同理，λ_N中第j个分量的检验数为：

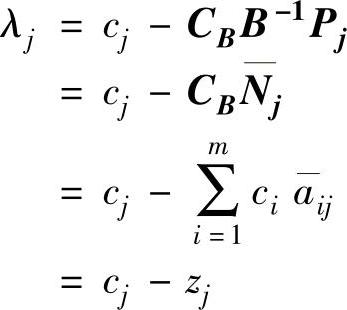
上面是假设可行基在前m列，在实际应用中可行基B由A中任意m列组成时，上述所有公式仍然有效。值得注意的是，在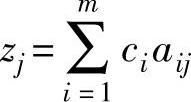中c_i不一定按c₁，c₂，…，c_m的顺序，下标的顺序要与基变量的下标一致。

【例1.17】 用公式计算下列线性规划的有关结果。

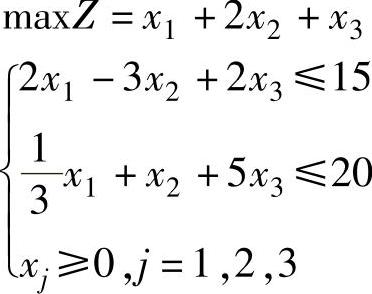
已知可行基。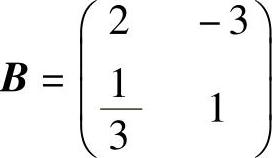

1）求基本可行解和目标值。

2）求单纯形乘子π。

3）B₁是否是最优基，为什么？

解 标准型为：

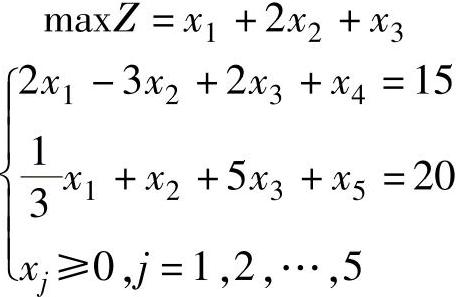
B₁由A中第1列、第2列组成，x₁、x₂为基变量，x₃、x₄、x₅为非基变量。故有C_B=

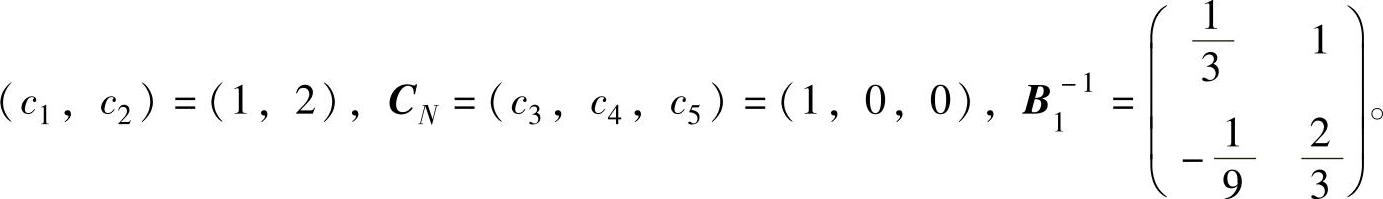
1）基变量的解为：

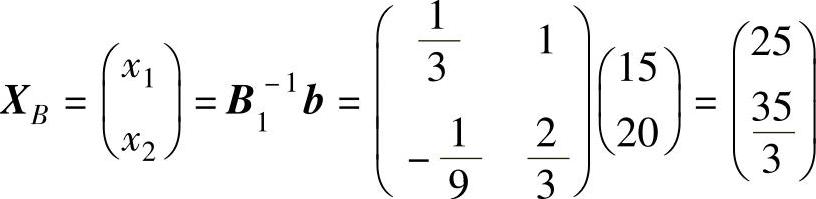
基本可行解为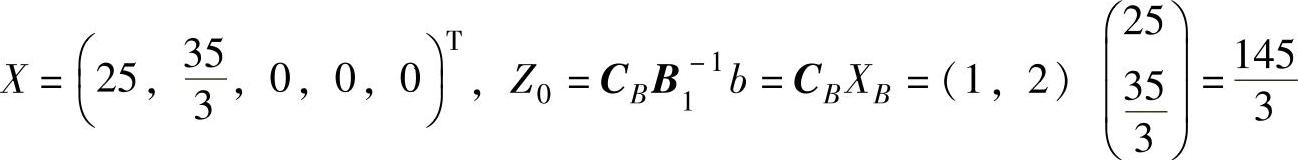

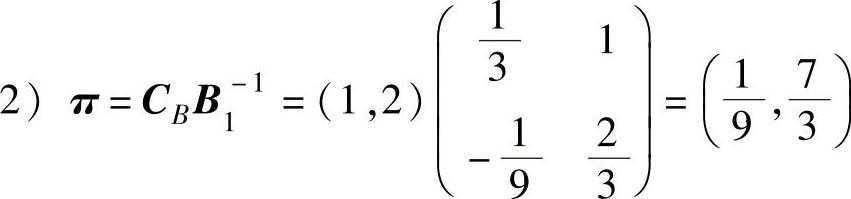
3）判断B₁是否是最优基，就要求出所有的检验数是否满足λ_j≤0（j=1，2，…，5）。由于x₁、x₂是基变量，故λ₁=0，λ₂=0。由λ_N计算公式得：

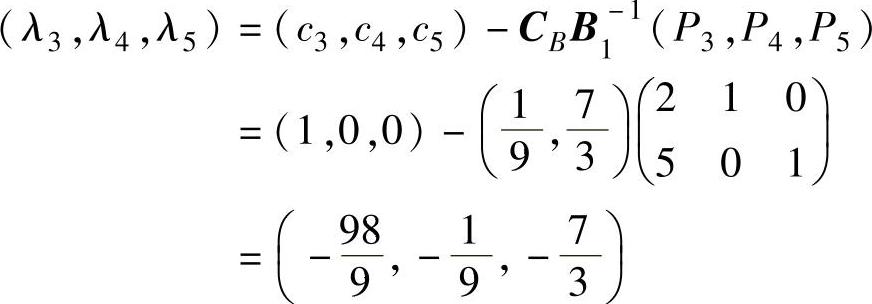
由于λ_j≤0（j=1，2，…，5），故B₁是最优基。