非对称信息条件下的连锁零售企业供应链模型

信息环节作为连锁零售企业供应链运作的重要基础，直接影响相关企业的计划、采购、制造、销售活动。在对称信息条件下，供应链采取的调控措施相对容易，而信息不透明、不平和条件下是供应链研究中的一个重大理论问题。

非对称的信息（AsymmetricInformation）作为经济领域常用的一个名词，在连锁零售企业供应链中主要是指其运行环节中，每个参与企业拥有的信息并不相同，企业对自身信息的掌握量远大于其他企业，这形成了供应链中信息的非对称性，另外随着大型垄断零售商所占市场份额的逐渐扩大，其在供应链中的强势地位也日益巩固。供应链中非对称信息的研究，近年来许多学者的关注并参与研究，但主要集中在需求或成本信息的非对称。如SUCKY（2006）研究了单个供应商和单个零售商的供应链在信息不对称情况下依靠转移支付实现供应链协调的讨价还价模型。姬小利等（2004）用委托代理理论设计了当销售价格为不对称信息时的VMI数量折扣契约。王晓斌等（2005）探讨了非对称需求信息下的两阶段供应链协调。其中秦娟娟等（2011）研究发现，供应链中成员利润为损失规避程度的减函数，信息对称情况下供应链中成员利润要优于非对称信息情况。最后，基于信号博弈探讨供应商风险偏好信息的揭示机制，证明信号博弈的分离均衡和混同均衡的存在，为供应商的决策提供了科学的指导。

当环境发生变化如机器故障、工人罢工、自然灾害和其他突发事件等时，供应链常常会受到不同程度的扰动，并最终影响供应链的决策。从非对称信息或供应链扰动单方面进行分析，近年来一些学者进行了初步的研究。王明照等（2008）分析了在非对称信息下供应链发生中断时供应商和销售商如何设计最优合同以降低自己的期望损失。其中周建中等（2013）对由一个生产商和一个销售商组成的两级供应链模型，在需求分别为线性和非线性情况下研究非对称信息下生产成本和市场规模同时发生扰动时，供应链中各成员的最优决策问题，可为供应链运行处于动态扰动情形下的稳定、可靠运行提供理论参考。

本节仅介绍需求函数分别为线性情形时，不对称信息下线性需求供应量链最优决策。

考虑由一个生产商和一个零售商组成的二级连锁零售企业供应链系统，如图5-6所示。商品的销售价格p和市场需求之间的关系是确切已知的，生产商生产的商品以w的批发价格卖给零售商。假设生产商和零售商都是独立的决策者，生产商是主导者，销售商是跟随者，它们的目标是争取各自利润的最大化。

图5-6 二级连锁零售企业供应链系统

假设生产商了解市场需求是零售价格p的线性函数Q（p）=a−kp（其中a表示市场规模，k表示价格敏感系数，且k＞0）知道a的波动范围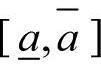但不能确定其具体值，其分布函数为F（a），密度函数为f（a），则均值可表示为。

要求满足约束条件：，e_a≥kc，c为生产商的单位生产成本。

除了市场规模a外，生产商与零售商共享其他信息。则在商品销售剩余量为0的条件下，即零售商根据小于市场需求的订货量订货，而生产商则依据零售商的订单组织生产，则此时生产商的产量等于零售商的销量，即Q（p）=a-kp。

在以上假设的模型中，通常依据生产商决定给零售商的批发价格w，零售商来决定小于市场需求的订货量及销售价格p。此时，零售商的利润为R_r（p）=（p-w）（a-kp），则最优销售价格为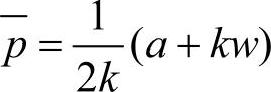，最优订货量为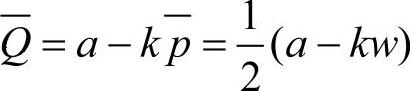；对于生产商，其期望利润为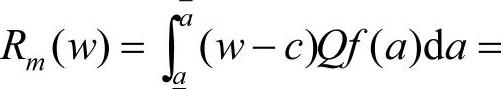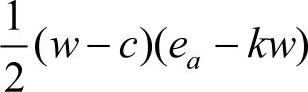，从而最优期望批发价格为，最优生产量为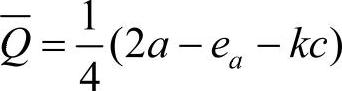。则相应的最优零售销售价格为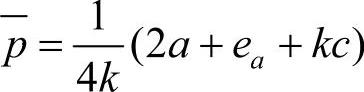，零售商的最大利润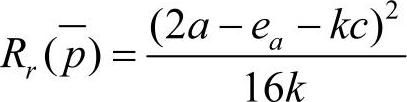，生产商的最大利润为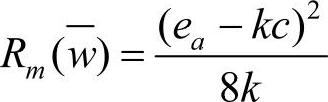，则，整条供应链的总利润为。

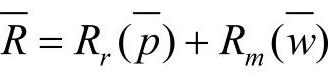考虑市场规模与生产成本同时发生扰动时供应链的收益、损失分析，有利于相应决策信息的制定与执行。假设市场规模与单位生产成本c同时发生扰动，其扰动量或改变量分别为Δa和Δc，则扰动后的市场规模和单位成本分别为a_d=a+Δa≥0和c_d=c+Δc≥0。令扰动发生后市场的需求量为Q_d（p）=a_d-kp，则相应的改变量为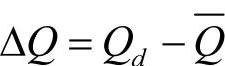，对应地，ΔQ＞0表示需要增加生产以满足市场的需求，ΔQ＜0表示产量过剩，有多余的原材料。

在信息不对称条件下，假设a_d的分布区间为，且有约束条件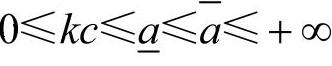。其先验分布函数和密度函数分别为G（a_d）和g（a_d），则对应的均值为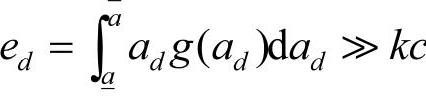。又假设生产商对a的估计值的改变量与其真实值的改变量相同，即e_d−e_a=a_d−a=Δa，那么当Δa≥0时表明市场需求规模增加，G（a+Δa）≥F（a）；当Δa≤0时，表明市场需求规模减小，G（a+Δa）≤F（a）。

市场规模发生变化时，零售商的利润为R_rd（p）=（p-w）（a_d-kp），对应的最优销售价格为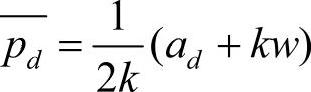，则订货量为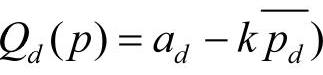。对生产商，生产成本发生变化时其期望利润为

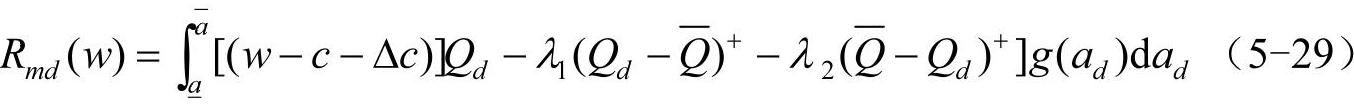
其中定义的函数（x）⁺=max（x，0），λ₁＞0为ΔQ＞0时多生产ΔQ的单位额外成本，λ₂＞0为ΔQ＜0时减少产量而发生的单位额外成本。上述表达式表明多生产一个单位的产品需要花费生产商λ₁个单位费用，而处理一个单位的缺货产品则会花费生产商λ₂个单位费用。

当需求增加时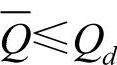，，由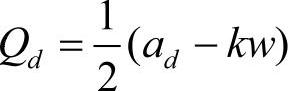可获得生产商的期望利润为

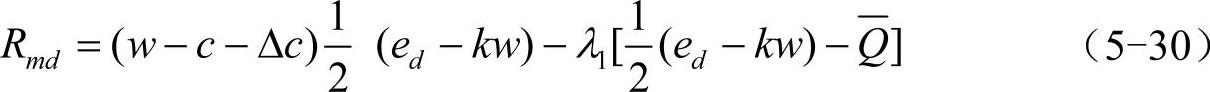
则极大化该期望利润的约束条件为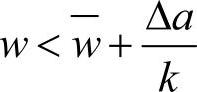，即。

由一阶必要条件得生产商的最优批发价为

对应的销售价为

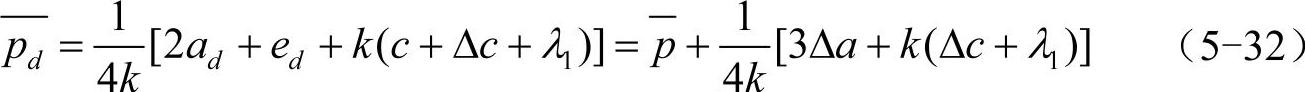(https://www.daowen.com)

订货量（即生产量）为

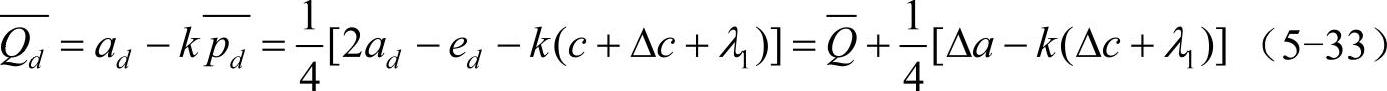
以下分两种情形

情形1：Δa＞k（Δc+λ₁）

这时必有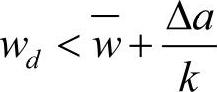，约束条件满足，表明生产商的期望利润函数在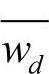处取最优，从而订货量为

即生产商最优产量增加。生产商的最优期望利润为

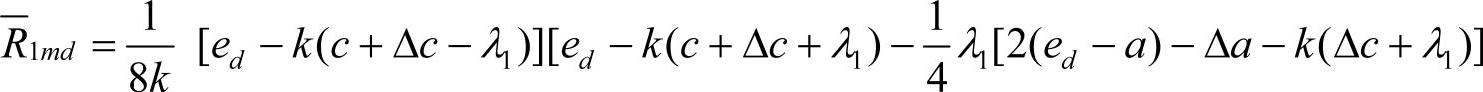
零售商的最优利润为

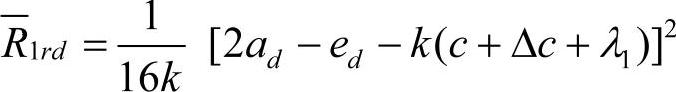
总的供应链利润为

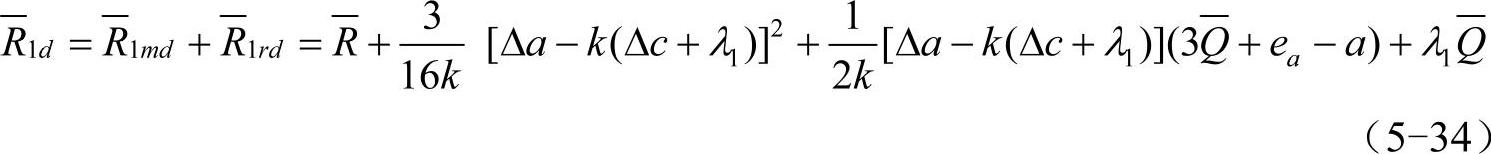
由于e_a≥kc及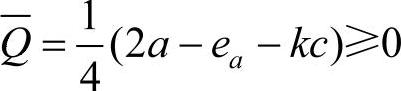，所以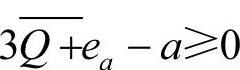，从而当Δa≥k（Δc+λ₁）时有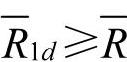。此表明，当市场规模与生产成本同时发生扰动且市场规模的扰动量和单位成本的扰动量满足关系Δa≥k（Δc+λ₁）时，产品生产量增加，同时供应链的总利润也增加。

情形2：kΔc＜Δa＜k（Δc+λ₁）

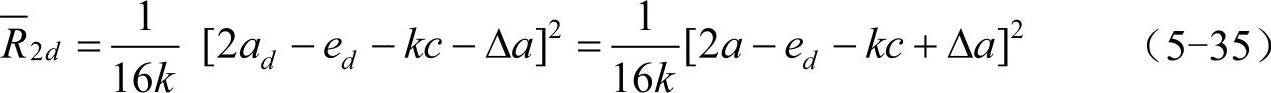
生产商的期望利润为

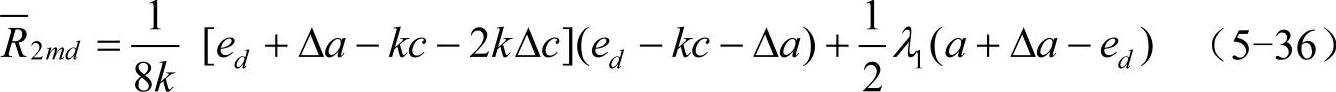
总的供应链的利润为

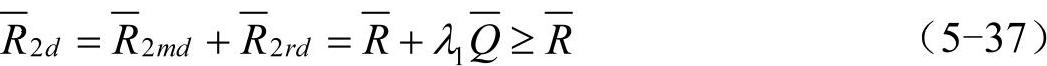
所以，当情形2条件满足时，虽然市场规模与生产成本同时发生扰动，但是产品生产量并没有发生变化，而供应链的期望总利润增加。

此外在需求减少时，可参照上述流程进行类似分析，具体情形分析可参阅周建中（2013）发表在中国管理科学的文献。