采用分数法求解问题的基本思想

分数法又称斐波纳契（Fibonacci）法，其基本思想与黄金分割法一样，不同的是在每次确定区间内点的位置时，采用斐波纳契数组成的分数作为区间的缩短系数。

所谓斐波纳契数F_n（n=0，1，2，3，…）是一个数列，其组成规律可由迭代公式表示：

利用上式可算出F_n的数列，见表3-2。

表3-2 斐波纳契数列

根据给定的允许误差ε＞0，F_n可由下式求出：

然后再由F_n在表3-2上查得对应的n及F_n-1和F_n-2。于是，第一次迭代公式为（图3-9）

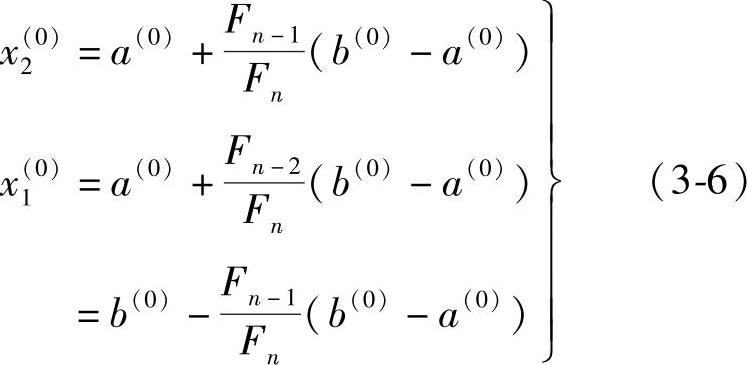
分数法的迭代步骤如下：

1）给定区间[a，b]（a＜b）及允许误差ε＞0。

图3-9 分数法原理示意图

2）置1⇒F₀，1⇒F₁。

3）判断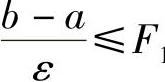是否成立，若成立则进行5），否则进行4）。

4）置F₀+F₁⇒F₁，F₁-F₀⇒F₀，返回3）。

5）置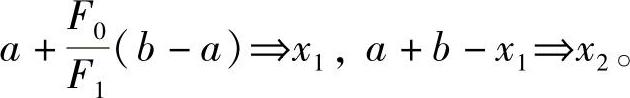

6）计算f（x₁）及f（x₂）之值，并置f（x₁）⇒f₁，f（x₂）⇒f₂。

7）检验是否满足条件b-a≤ε。若满足，则比较f₂与f₁。当f₂＞f₁时，输出x₁、f1为近似最优解；否则输出x₂、f₁为近似最优解，均停止迭代。若不满足条件：b-a≤ε，则进行8）。

8）比较是否满足不等式f₂＞f₁，若满足，置x₂⇒b，x₁⇒x₂，a+b-x₂⇒x₁，f₁⇒f₂，f（x₁）⇒f₁，返回进行7）；否则，置x₁⇒a，x₂⇒x₁，a+b-x₁⇒x₂，f₂⇒f₁，f（x₂）⇒f₂，返回进行7）。

分数法的迭代过程如图3-10所示。

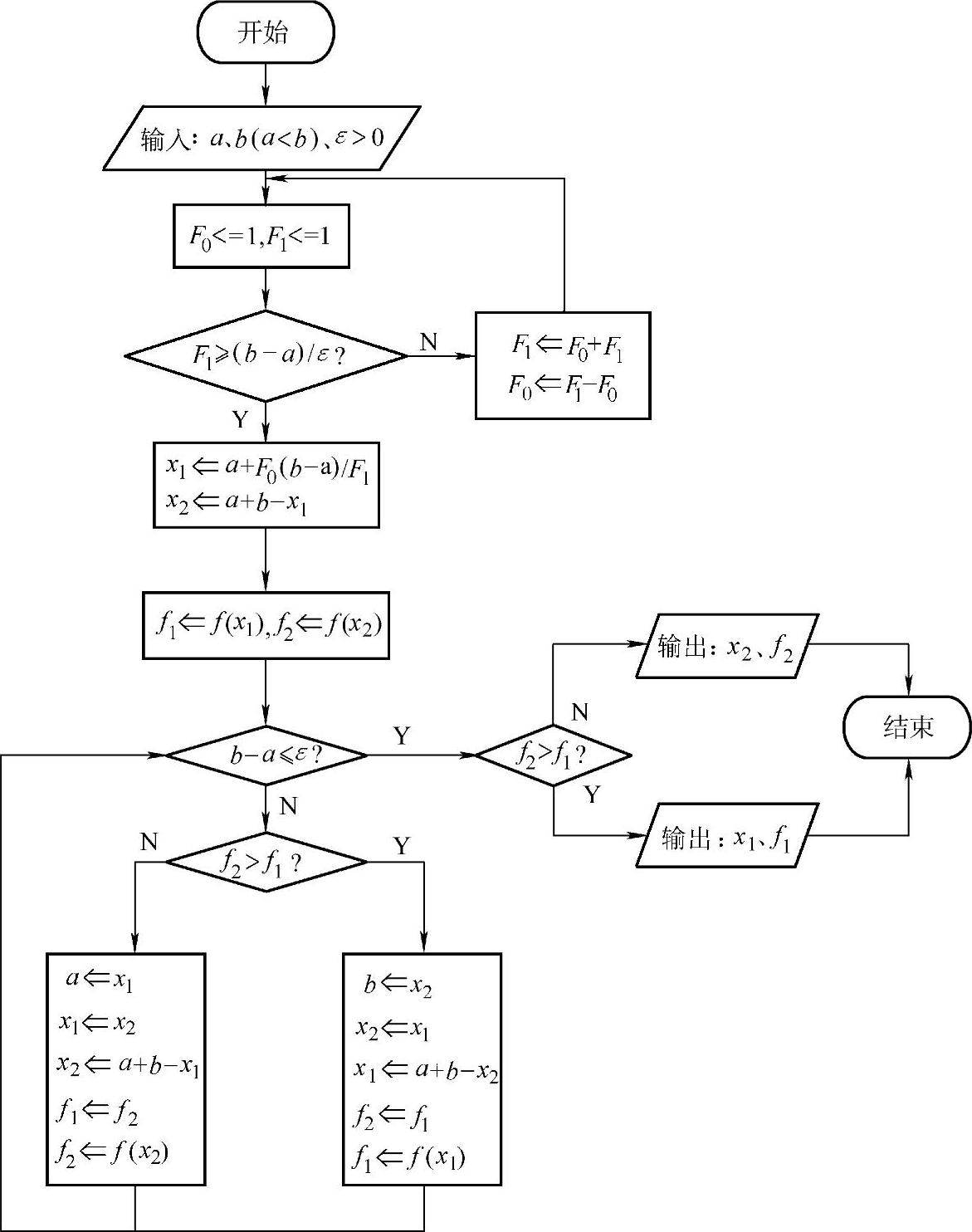
图3-10 分数法程序框图

【例3-4】已知汽车行驶速度x与每千米耗油量的关系为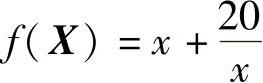，试用分数法求当速度x在0.2～1km/min范围内的最经济速度X^*。

解 依题意知[a^（0），b^（0）]=[0.2，1]，设ε=0.1。因为

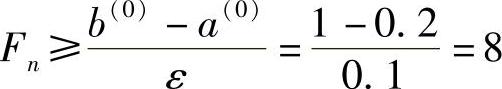
查表3-2得n=5。

第一次迭代计算：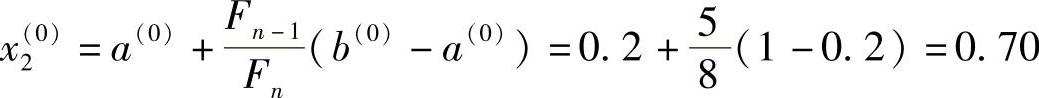

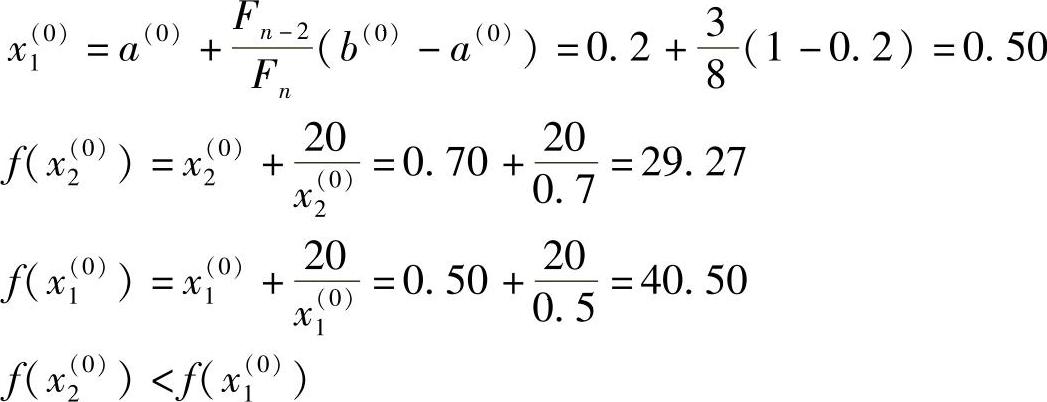
第二次迭代计算：

取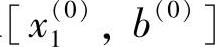为新区间，即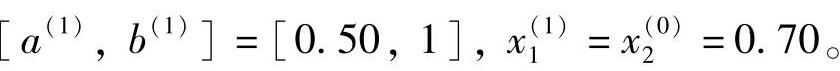于是(https://www.daowen.com)

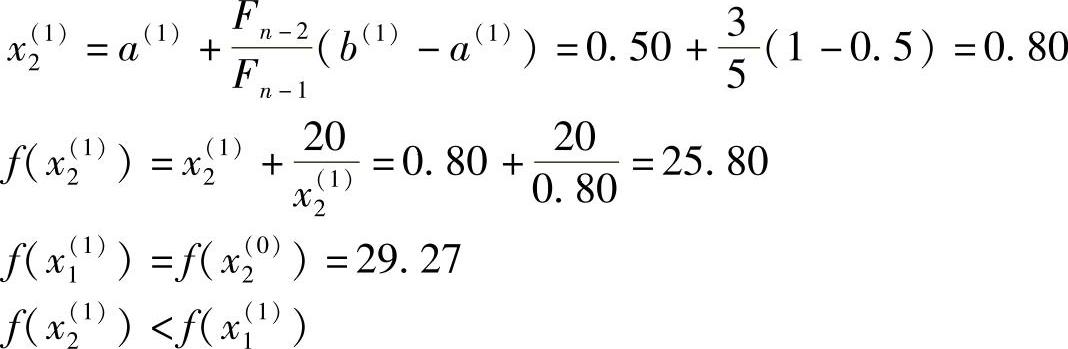
以此类推。当进行到第k次时，其迭代公式如下：

1）类似图3-9b情况时：

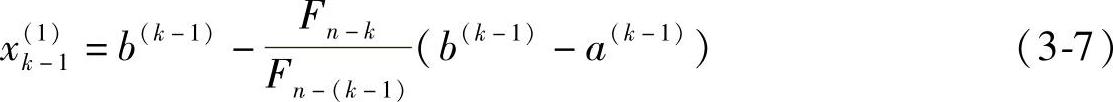
2）类似图3-9c情况时：

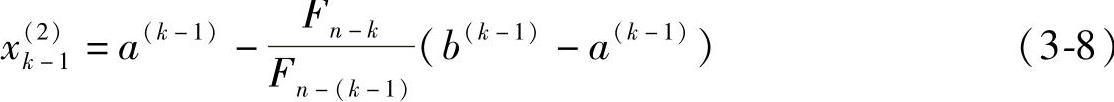
第三次迭代计算：

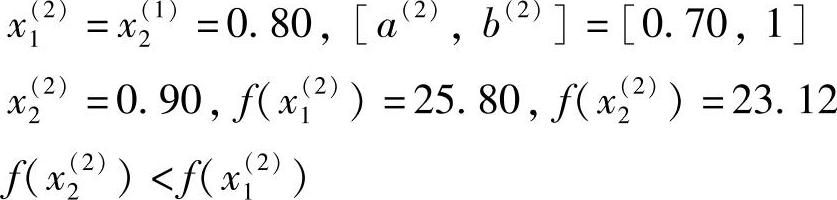
第四次迭代计算：

取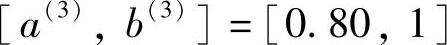。因为k=n-1=4，此时斐波纳契分数是

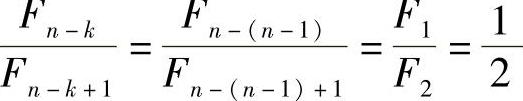
在区间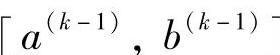中，两个计算点将重合，无法进一步比较其函数值的大小，可改用下式：

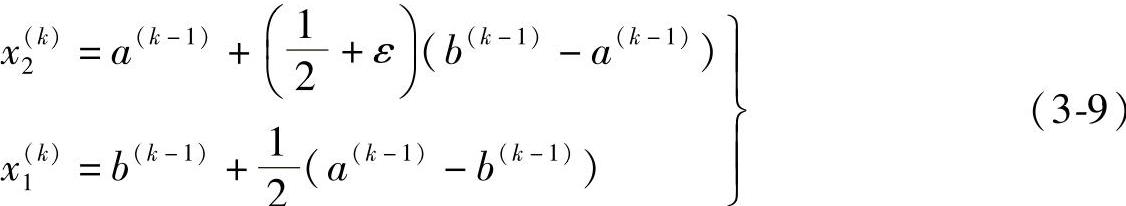
计算，于是

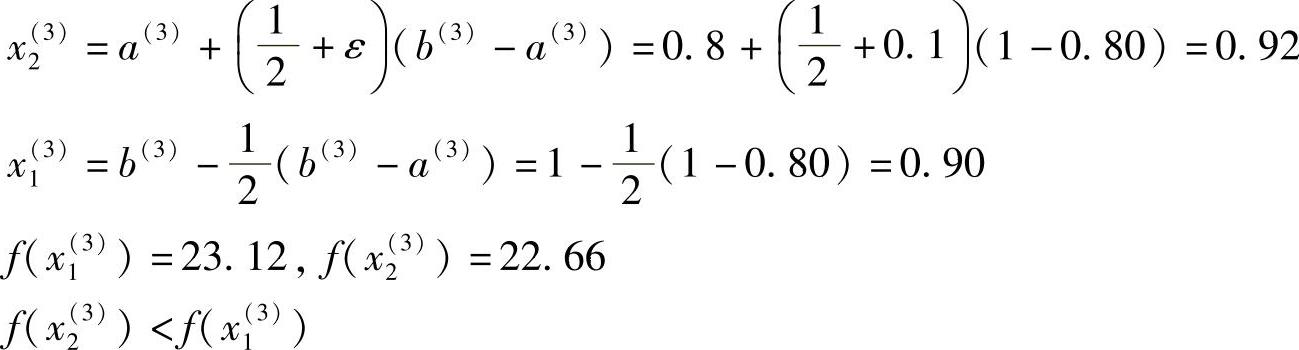
第五次迭代计算：

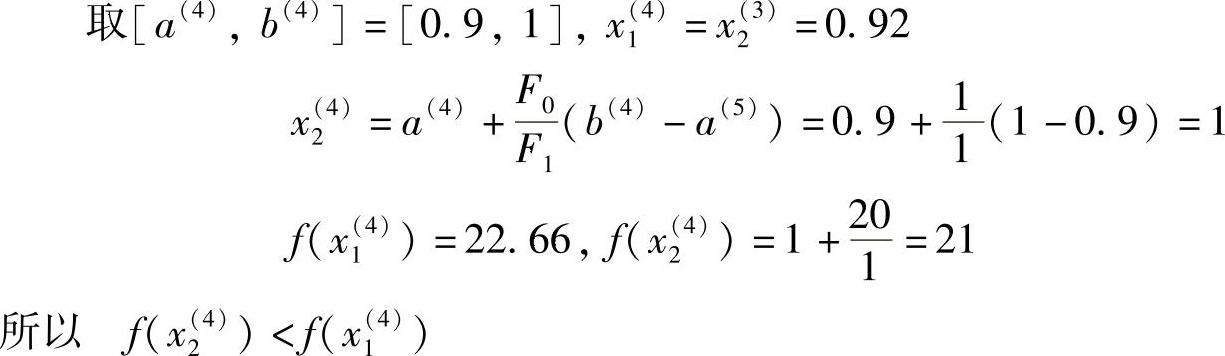
这时精度要求已满足，即b^（4）-a^（4）=1-0.90=0.1=ε

故汽车行驶的最经济速度为：X^*=x₂^（4）=1（km/min）。

从前面讨论可以看出，分数法和黄金分割法（0.618法）的迭代过程基本上是相同的，所不同的仅有一下两点：

1）分数法首先要确定函数值的计算次数n。n一旦确定之后就不能更改，否则要重新计算。

2）分数法每次缩短的比例是变化的，即分别为

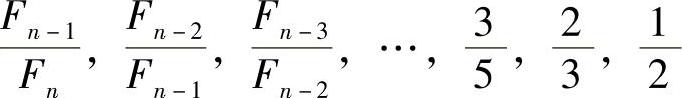
而黄金分割法中的缩短比例为常数0.618，同时还可以看到：

当n=9时，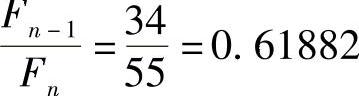

当n=10时，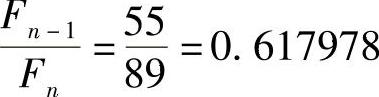

当n=11时，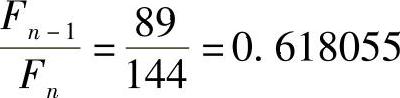

当n=12时，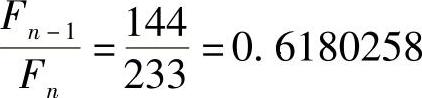

还可以证明当n很大时，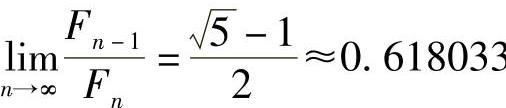

由此可以看出，黄金分割法是分数法的极限情况。综上所述，就理论上而言，分数法优于黄金分割法，但由于黄金分割法实现起来简单易行，且一般能满足机械设计的精度要求，因而实际上多采用黄金分割法。