混合惩罚函数法优化算法

混合惩罚函数法的思想很简单，就是对不等式约束用内点惩罚函数法，而对等式约束用外点惩罚函数法。这样可克服两种惩罚函数法的某些限制，如内点惩罚函数法不能用于非可行域内点的情况，外点惩罚函数法不能用于在可行域外部某些约束无定义或病态的情况。

对于兼有等式和不等式约束条件的最优化问题，采用如下形式的混合惩罚函数：

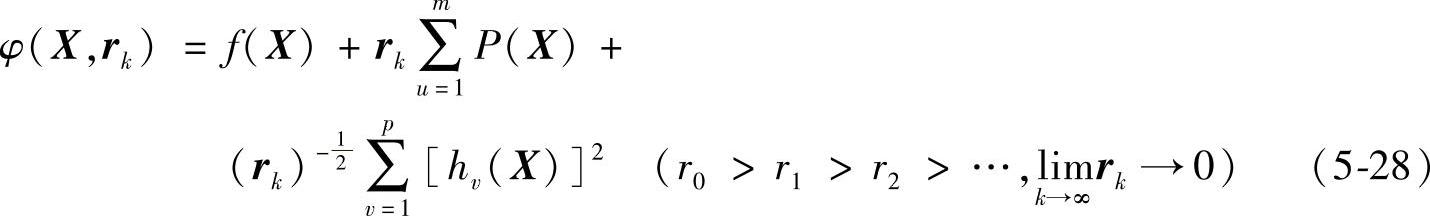
这里将惩罚因子统一用r_k，且要求不等式约束的可行域应至少有一个内点。

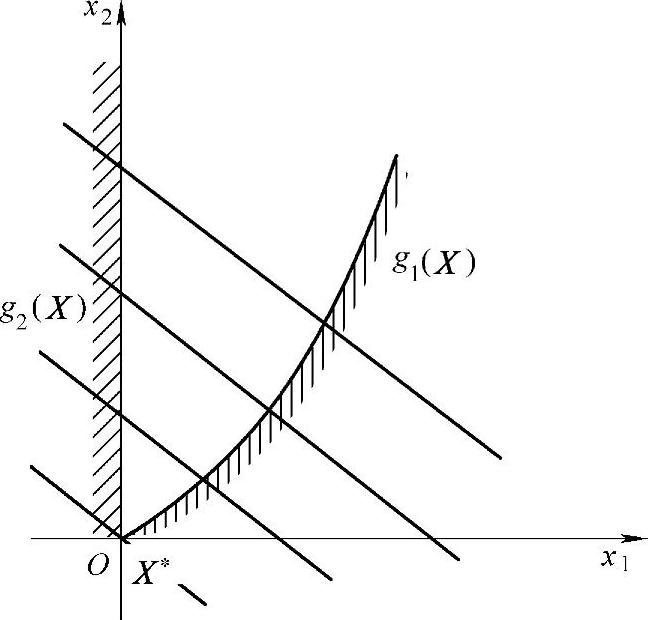
图5-9 例5-7解的几何表示

混合惩罚函数法的计算步骤如下：

1）选择满足不等式约束的一个内点X^（0）作为起始点，并选择适当的r₁＞0，给定小量ε₁＞0，ε₂＞0，令k=1。

2）以X^（k-1）作为起始点，用无约束最优化算法求φ（X，r_k）的最小点X^（k）=X（r_k）。

3）检查|X^（k）-X^（k-1）|≤ε₁与|f（X^（k））-f（X^（k-1））|≤ε₂。

4）如果满足3）的收敛准则，则终止计算，取X=X（k）；否则，令r_k+1=r_k/C，其中C是大于1的数。令k=k+1后返回2）。

这种混合惩罚函数法比之单纯使用外点惩罚函数法有加速迭代过程的收敛作用。

混合惩罚函数法的迭代过程如图5-10所示。

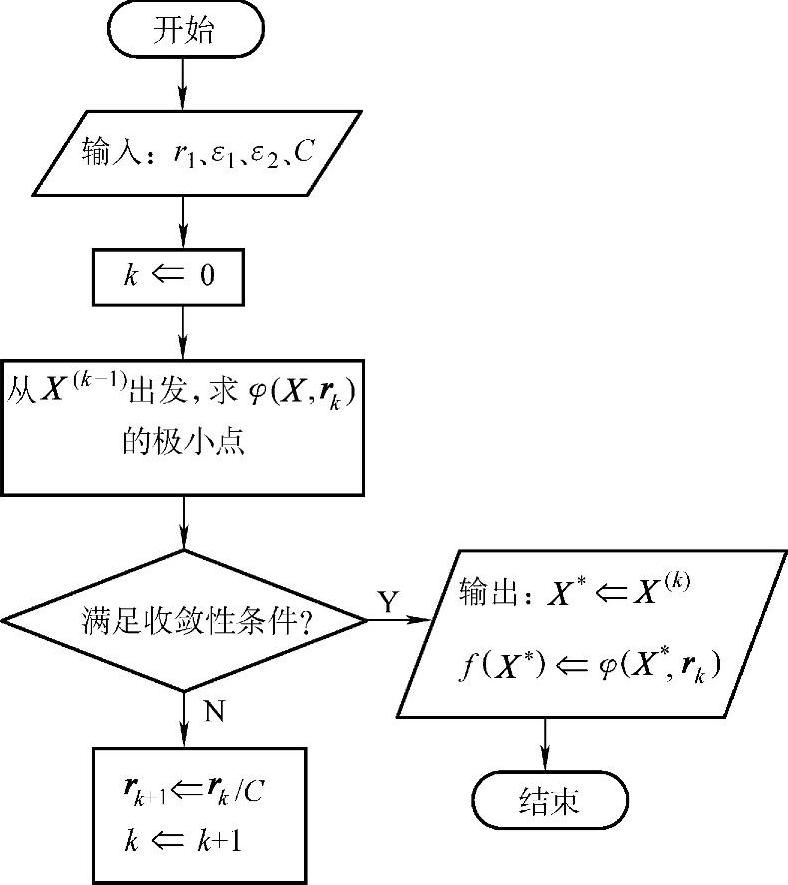
图5-10 混合惩罚函数法程序框图

【例5-8】试用混和惩罚函数法求解目标函数f（X）=-x₁+x₂在约束条件h（X）=x₁+x₂-1=0和g（X）=-lnx₂≤0下的最优解。

解 由于g（X）在X=0时无界，故不能用外点惩罚函数法处理；又由于h（X）没有内点，亦不能用内点惩罚函数法处理。因而，只能用混合惩罚函数法求解本问题。

如式（5-28）的目标函数是：

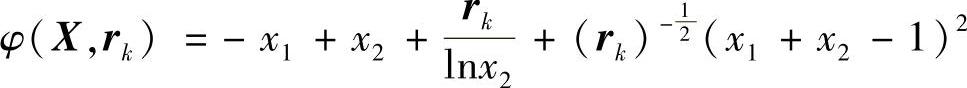
最优解的必要条件是：(https://www.daowen.com)

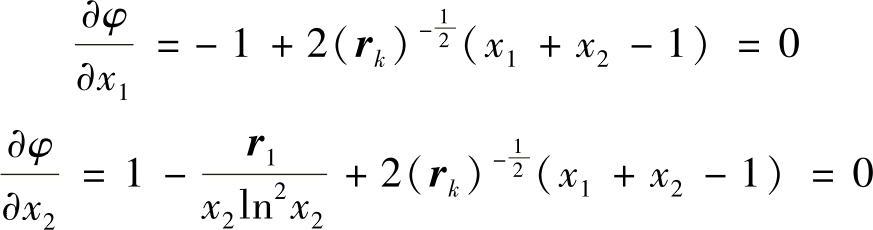
两式相减，得

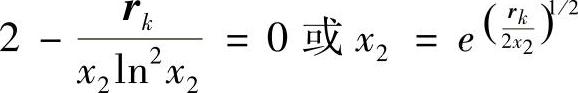
当r_k→0时，x₂→l，且必须满足（x₁+x₂-1）→0，否则将违反约束h(X)。因此在取极限时得x₁=0。这样，该问题的最优解为X=[0，l]^T，f(X)=1。

式(5-28)是不等式约束部分按内点法形式处理的混合法，故称之为内点形式的混合法。若不等式约束部分按外点法形式处理，即外点形式的混合法，其惩罚函数形式为

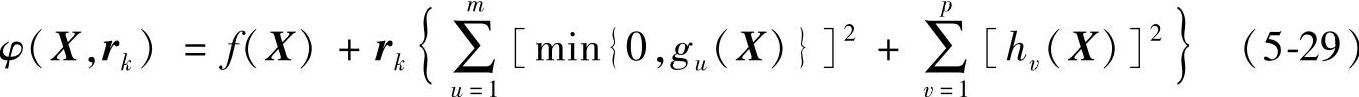
惩罚因子r_k恒为正，且r_k+1=Cr_k；递增系数C＞1，且有

。

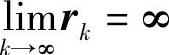初始点可在E空间任意选取，初始惩罚因子r₀、递增系数可参照外点法选取。

5.6.5 讨论

如前所述，惩罚函数法有内点法、外点法与混和法之分，不同方法的惩罚函数形式也不同。但是，它们仍能归结为如下统一的惩罚函数形式：

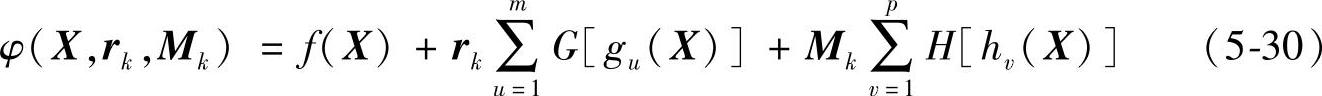
式中

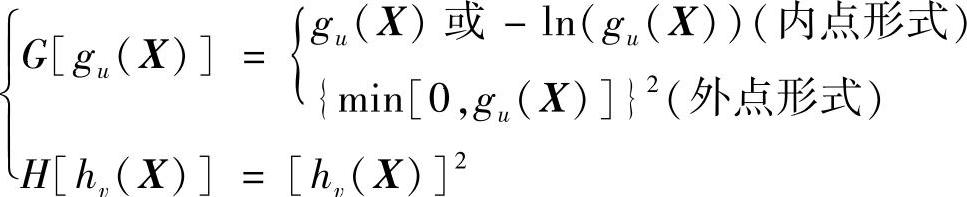
从解决问题的范围和惩罚函数的构造方式来看，内点法和外点法可以看作是混和法的特殊情况。无论哪一种形式，惩罚项的函数值总为正。因而有φ(X，r_k)≥f(X)。为使φ(X，r_k)最终能收敛到f(X)的同一最优解，可通过对参数r_k、M_k。的不断调整，使其惩罚项对f(X)的惩罚作用在搜索过程中趋于减弱并终将消失。为此，惩罚项必须具有如下性质：

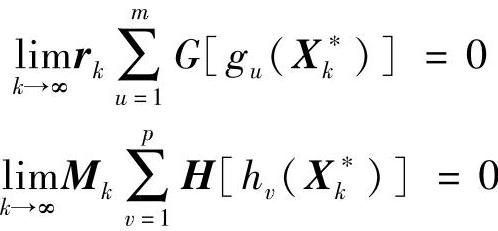
从而必存在关系：

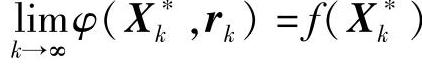
由此表明，惩罚函数法是用惩罚函数妒φ(X，r_k)去模拟原目标函数f(X)的一种函数逼近过程。