Martinelli-Nelson方法详解

Martinelli和Nelson处理了蒸汽-水的数据。他们的基本假设是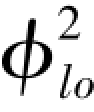可以在任何压力条件下都与流动干度关联起来。热力学平衡及流动处于湍流-湍流状态。使用Lockhart-Martinelli的Xtt（湍流-湍流）的结果，建立了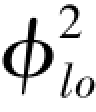的关联（图4-24）。

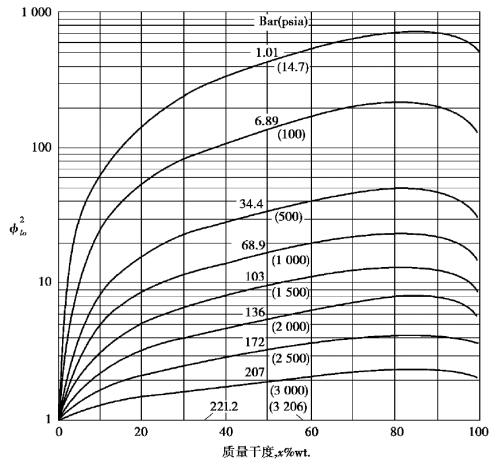
图4-24　Martinelli-Nelson的将φ2
lo作为干度和压力的函数

Jones给出了蒸汽-水的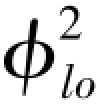分析值：

注意该方法假设在采用均相流模型时，质量流速不影响。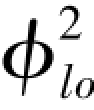

在计算加热通道的总压降时，摩擦压降需要根据平均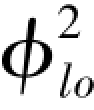来计算：

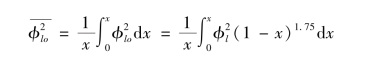
或者

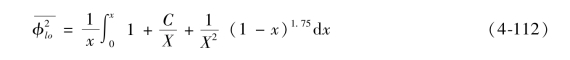
在Xtt（C=20）下采用Martinelli-Nelson方法所得到的结果如图4-25所示。

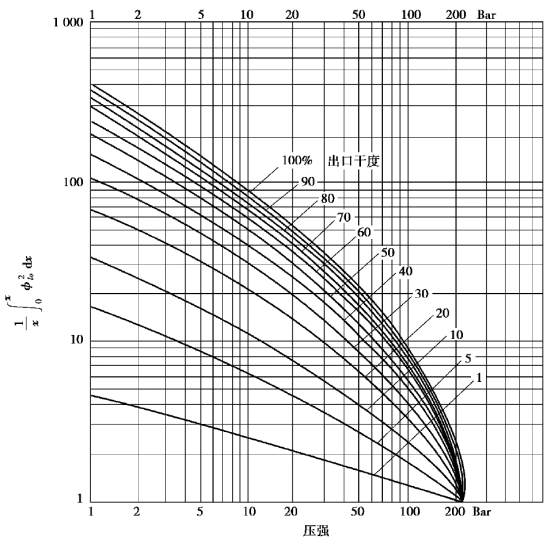
图4-25　在入口干度为0下采用Martinelli-Nelson方法所得到平均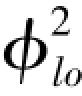

积分式（4-97），并忽略蒸汽的压缩性得到

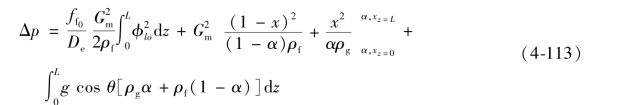(https://www.daowen.com)

在z=0时，α=x=0，在整个加热长度L热流密度不变，则在全长方向蒸汽干度线性增加：

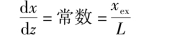
因此式（4-113）可以写为

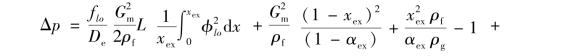
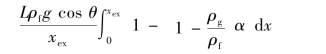
或

式中，参数r3为基于全液相流动的长度平均两相流摩擦压降倍数。在轴向均匀加热条件下，r3等于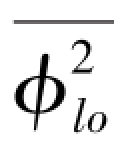，可以用式（4-112）来计算。α值与干度的关系示于图4-26中。r2取值在大气压和出口干度在1%～100%的条件下从2.3到1 500，在7.0 MPa下从0.2到20。

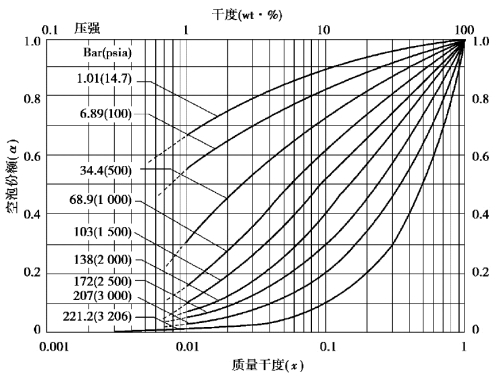
图4-26　Martinelli-Nelson方法的空泡份额

式（4-114）的形式对于预测更为普遍加热方式下的压降情形很有用处，也可以使用其他的模型。然而，r2，r3和r4的值对于非均匀加热的情况和采用不同的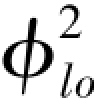及α的模型时是不同的。

需要认识到Martinelli-Nelson方法和均相流模型的一些不足之处：

①它们都忽略了在给定干度条件下质量流速（Gm）对压降梯度的影响，然而实验发现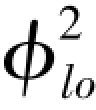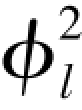，和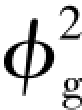与质量流速Gm有关。

②它们都没有考虑表面张力效应，在高压下还非常重要（特别是接近临界点时）。

各研究者发现在500<Gm<1 000 kg/（m2·s）下，Martinelli-Nelson结果比均相流模型好；但在Gm=2 000 kg/（m2·s）时，均相流模型要好一些。该结果的原因可能是在给定干度下高流速两相流混合更为均匀所致。