用相量法求同频率正弦量之和

只有同频率正弦量的相量才能相互运算。用相量表示正弦量进行交流电路运算的方法称为相量法。用相量法分析正弦交流电路十分方便，下面举例加以说明。

例如，一条支路上有两个同频率的正弦电压，其解析式为

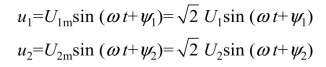
相量的运算

利用三角函数知识计算，可以得出它们的和为同频率的正弦量，即

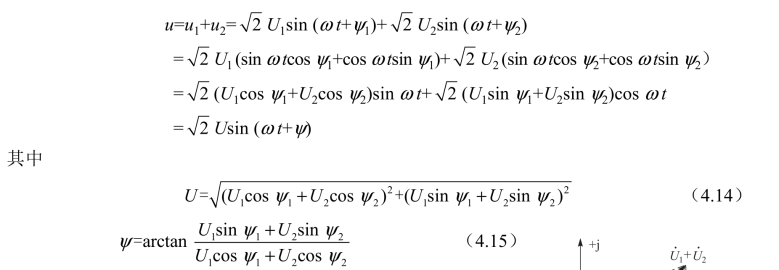
可以看出，要求出同频率正弦量之和，关键是求出它的有效值和初相。但用三角函数运算很麻烦，用相量法求和就方便得多。

现在复平面上作出相量按平行四边形法则作出的相量图，如图4-18所示。从相量图中各相量之间的几何关系得

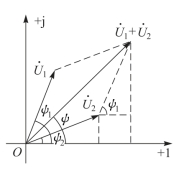
图4-18　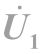+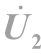的相量图

可见，相量相加所得的模、辐角与解析式相加所得的有效值、初相相同。(https://www.daowen.com)

由此可以得到一个重要结论：

因此，同频率正弦量相加的问题可以转化成对应的相量相加，用这种方法形象且直观。其步骤为：

①由相加的正弦量的解析式写出相应的相量，并表示成代数形式。

② 按复数运算法则进行相量相加，求出和的相量。

③由和的相量的有效值和初相写出和的正弦量。还可以作相量图，按照矢量的运算法则求相量和。

例4.10 已知两个同频率的正弦电压求它们的和u1+u2，并画相量图。

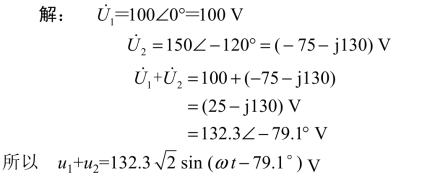
其相量图如图4-19所示。

注意：u1与u2之和的有效值不等于u1的有效值加u2的有效值。

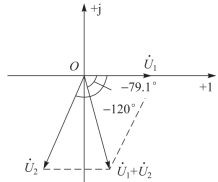
图4-19　例4.10相量图