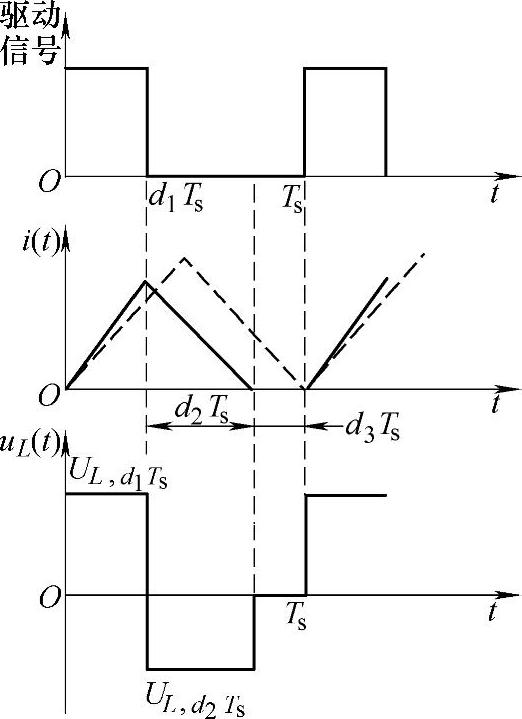
图1-35 DCM的波形示意图
理想Buck变换器如图1-1所示。下面按照1.2.2小节的三个步骤用状态空间平均法分析DCM下的理想Buck变换器。
1.列写三阶段状态方程和电感电流平均变量方程
选电感电流i(t)和输出电压u(t)作为状态变量,选输入电流ig(t)作为输出变量。DCM下理想Buck变换器的三种工作状态如图1-36所示。
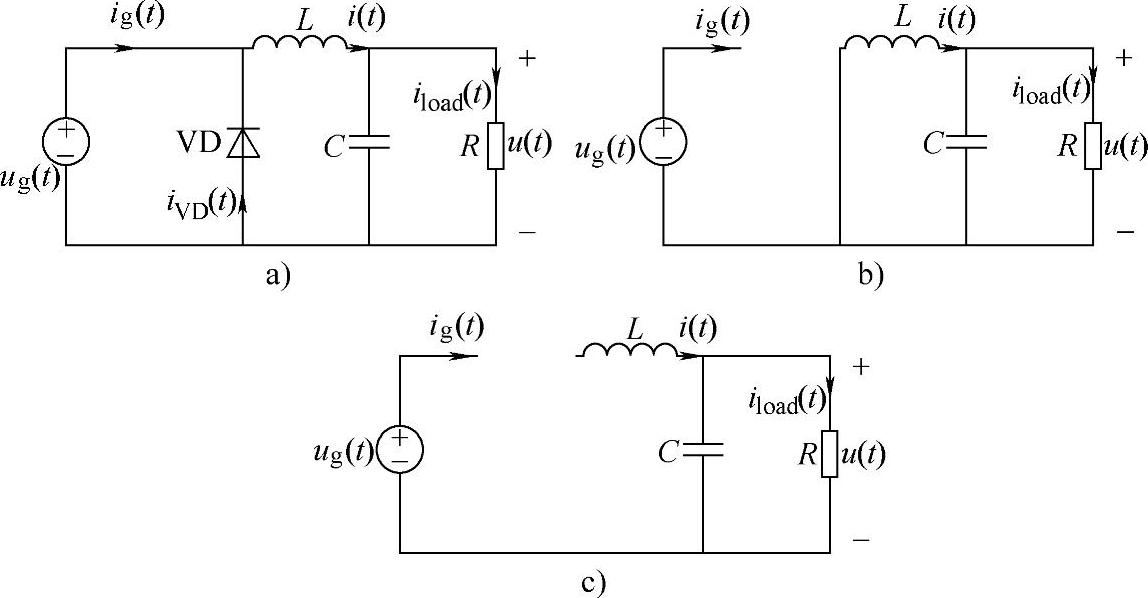
图1-36 理想Buck变换器DCM下三种工作状态
a)工作状态1 b)工作状态2 c)工作状态3
对DCM下DC-DC变换器的三个工作状态分别列写状态方程与输出方程如下:
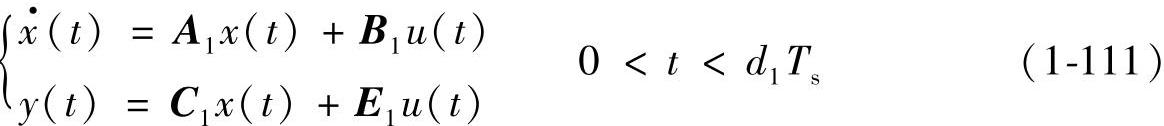
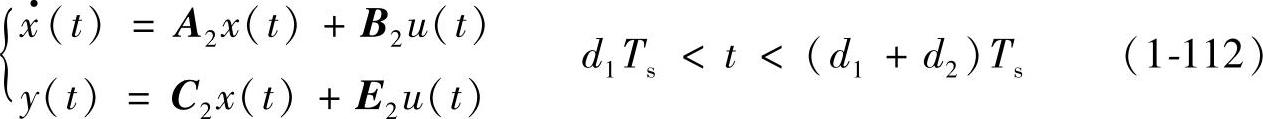
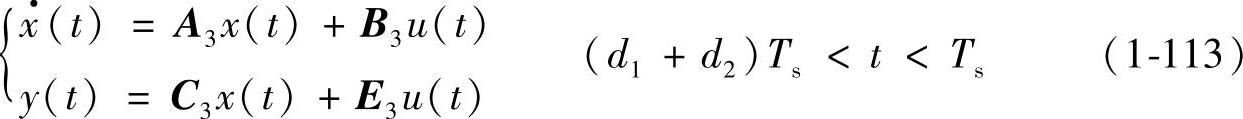
电感电流平均变量方程为
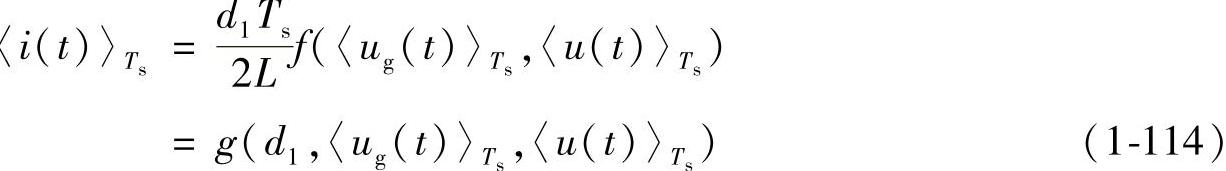
式中,函数f(<ug(t)>Ts,<u(t)>Ts)为用<ug(t)>Ts和<u(t)>Ts表达的(0,d1Ts)时间段内的电感电压,即图1-35中所示的UL,d1Ts,f一般为<ug(t)>Ts与<u(t)>Ts的线性函数。
工作状态1:开关器件VF导通,二极管VD截止,电路如图1-36a所示,变换器的状态方程与输出方程如下:
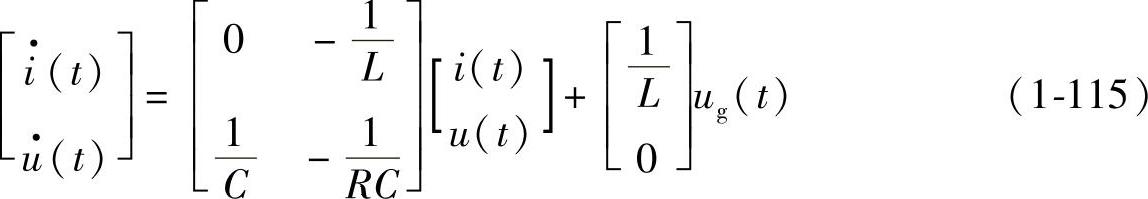
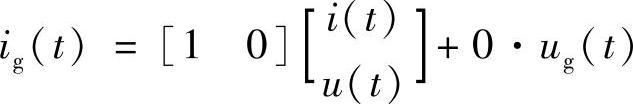
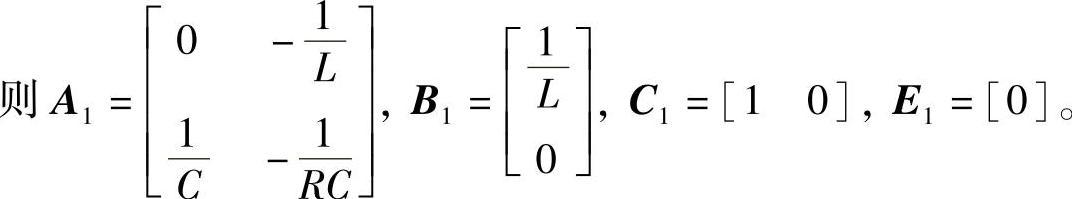
工作状态2:开关器件VF截止,二极管VD导通,电路如图1-36b所示,变换器的状态方程与输出方程如下:
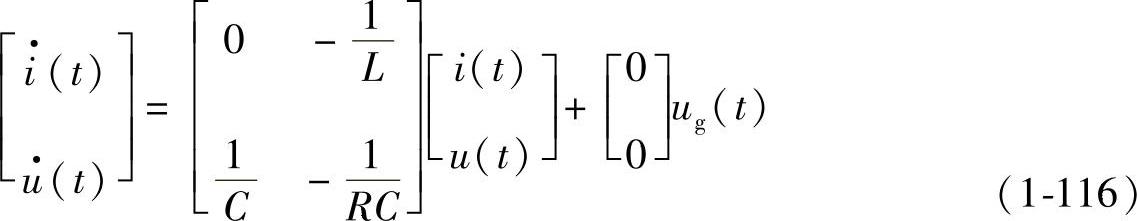
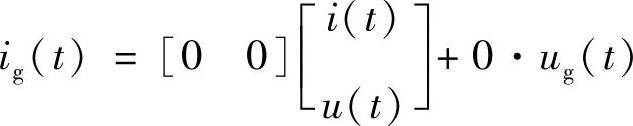
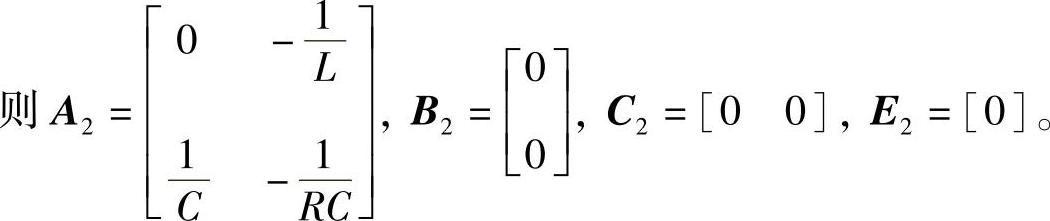
工作状态3:开关器件VF与二极管VD都截止,电路如图1-36c所示,变换器的状态方程与输出方程如下:
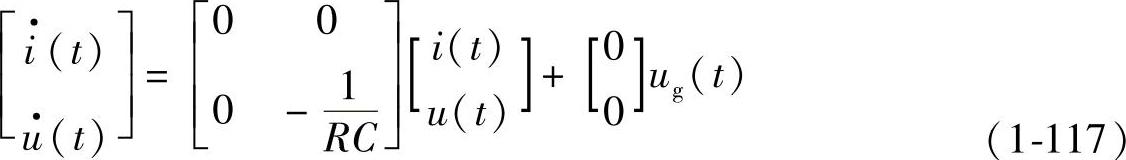
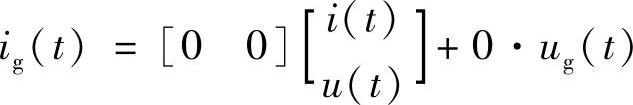
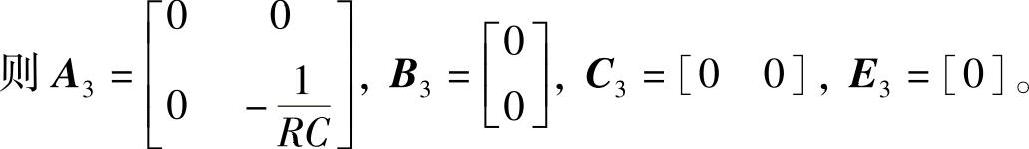
列写电感电流平均变量方程,可根据图1-35a用<ug(t)>Ts和<u(t)>Ts表达的(0,d1Ts)时间段内的电感电压为
UL,d1Ts=f(<ug(t)>Ts,<u(t)>Ts)=<ug(t)>Ts-<u(t)>Ts (1-118)则电感电流在(0,(d1+d2)Ts)时间段内的平均值为
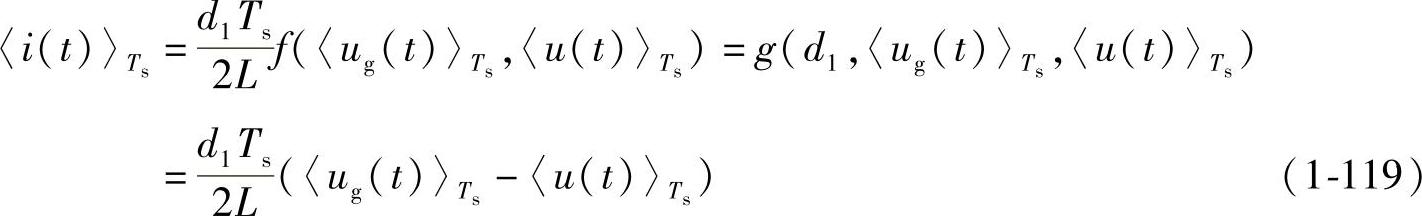
2.确定静态工作点和D2
根据分段列写的状态方程与输出方程可得到
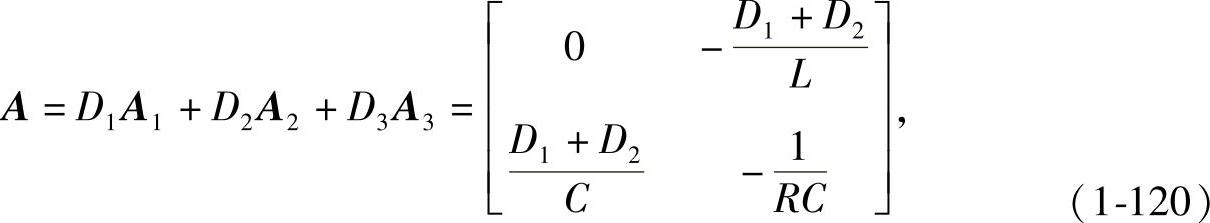
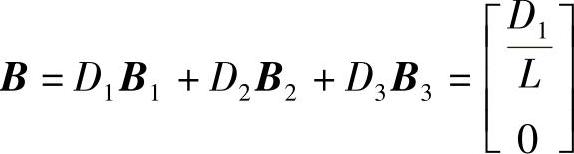
C=D1C1+D2C2+D3C3=[D10],
E=D1E1+D2E2+D3E3=[0]式中,D3=1-D1-D2。
变换器的稳态方程组为
AX+BU=0
Y=CX+EU (1-121)(https://www.daowen.com)
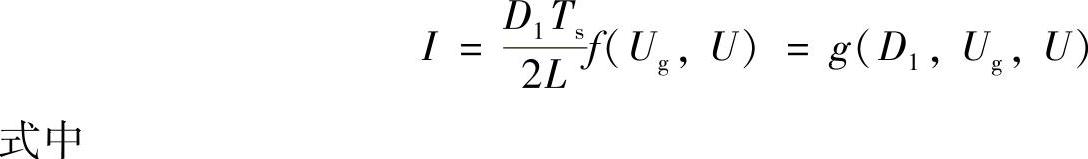
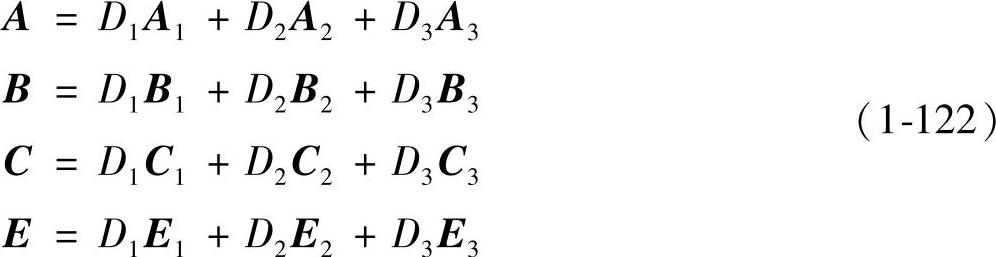
根据式(1-121)可以得到变换器的稳态方程组为
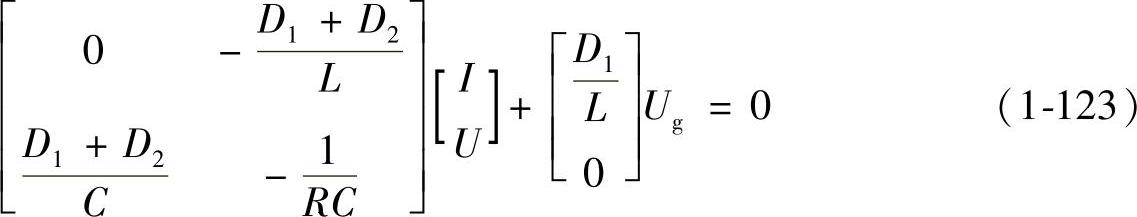
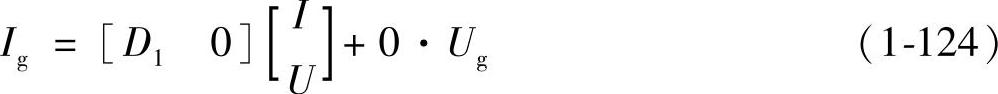

由式(1-123)可得到
-(D1+D2)U+D1Ug=0 (1-126)

由式(1-126)可得到用D1和D2表示的电压比M

根据式(1-125)~式(1-128)可解得未知量D2、I、Ig和电压比M,分别为
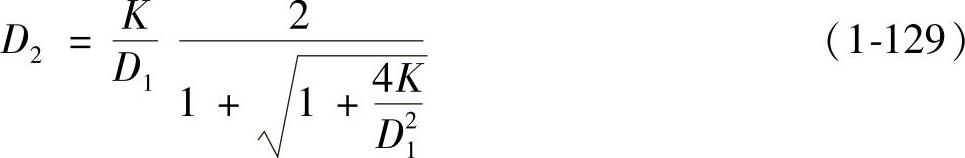

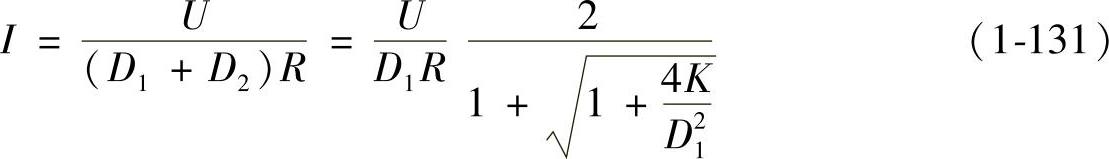
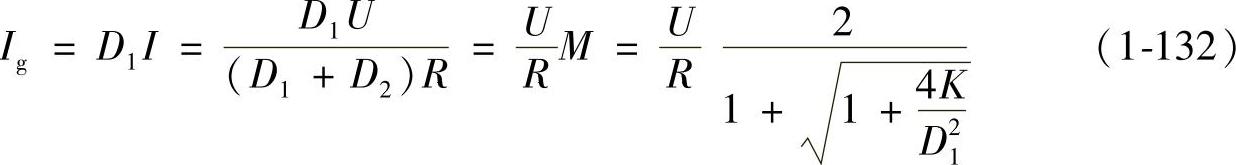
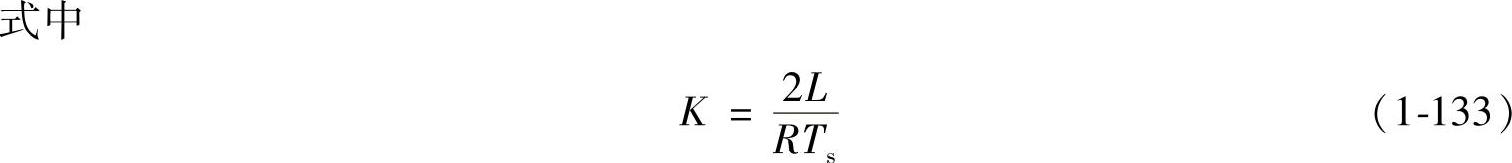
K是DCM下变换器的一个重要参数。
当变换器运行在闭环情况下时,对于一给定的变换器,M、K和U已知,将D1、D2和I表达为M、K和U的函数可便于确定系统的控制策略。这时D1、D2和I的表达式分别为



需注意的是电流I所描述的是(0,(d1+d2)Ts)时间段内电感电流的直流分量。
3.建立交流小信号状态方程与输出方程
交流小信号的状态方程与输出方程为
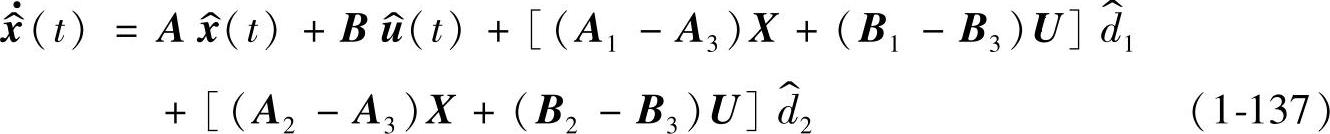
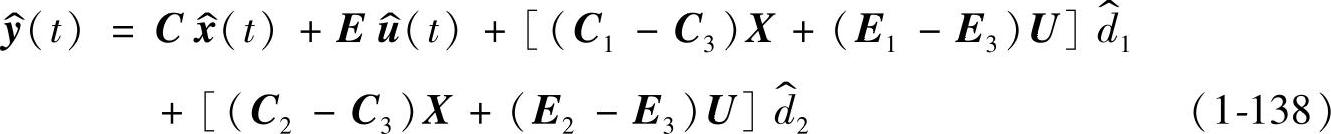
则理想Buck变换器的交流小信号的状态方程与输出方程为
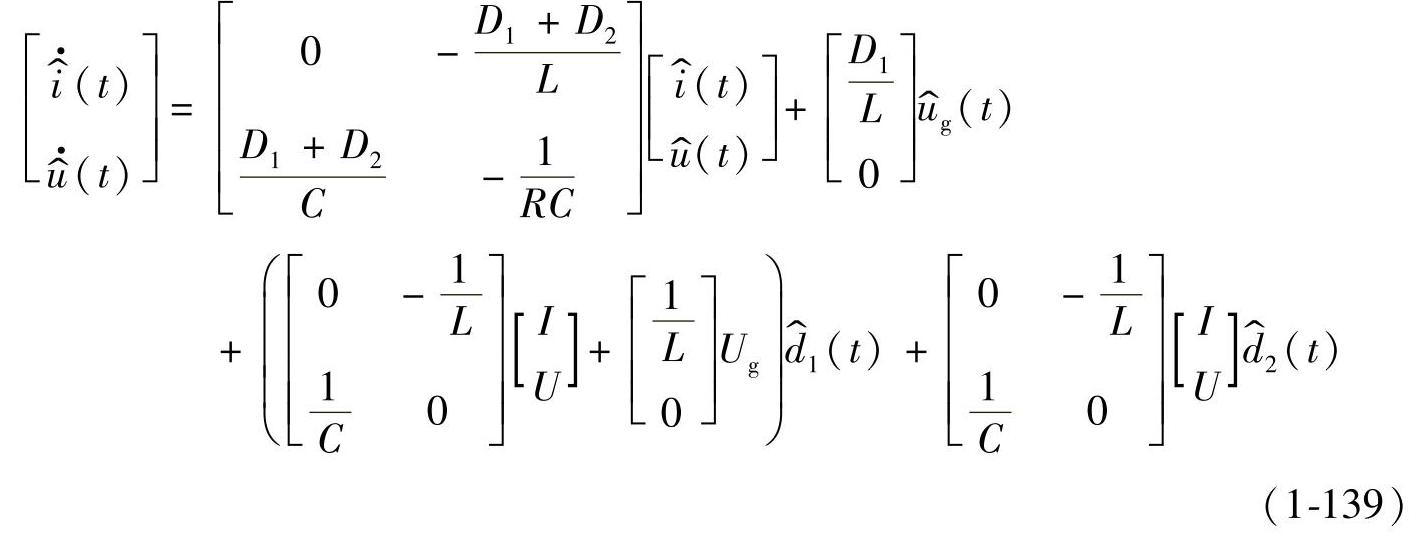
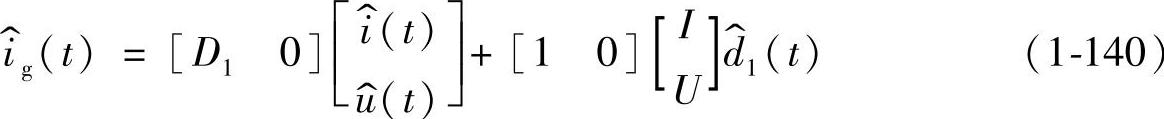
由电感电流提供的辅助方程为

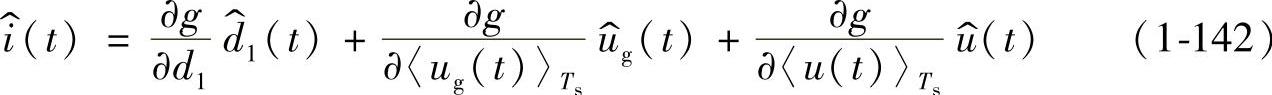
所以有
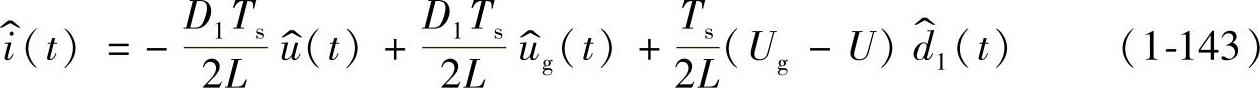
式(1-139)、式(1-140)、式(1-143)为理想Buck变换器的交流小信号方程组,这里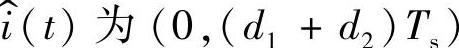 时间段内电感电流的交流分量。联立式(1-139)、式(1-140)、式(1-143)可求得各小信号变量。为了便于建立变换器的DCM下小信号等效电路和分析变换器的DCM下低频动态特性,一般将
时间段内电感电流的交流分量。联立式(1-139)、式(1-140)、式(1-143)可求得各小信号变量。为了便于建立变换器的DCM下小信号等效电路和分析变换器的DCM下低频动态特性,一般将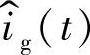 和
和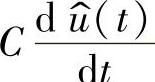 表示成
表示成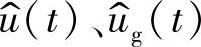 和
和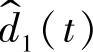 的函数,因此,
的函数,因此,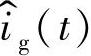 和
和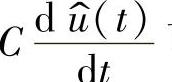 可表示为
可表示为
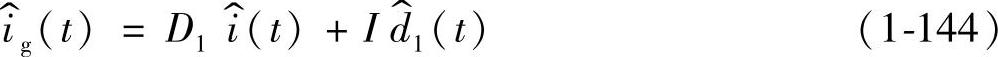
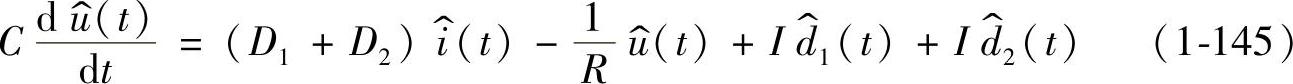
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







