基本概念：哈密尔顿算子与涡量连续性微分方程

（1）涡量Ω

设流体微团的旋转角速度为ω（x，y，z，t），则涡量定义为

Ω，ω都反映流体质点瞬时转动的转动方向。其中，Ωx、Ωy、Ωz是涡量Ω在x，y，z坐标上的投影。由定义可知

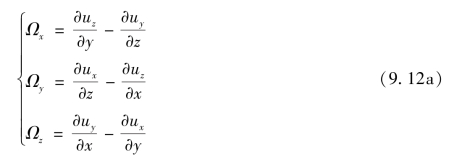
显然，涡量同速度一样也是空间坐标和时间的函数：Ω＝Ω（x，y，z，t）。所以，它也构成一个向量场，称为涡量场。哈密尔顿算子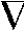是一个矢性微分算子，即

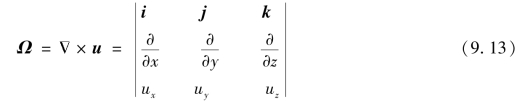
从而

或

上式称为涡量连续性微分方程。

（2）涡线、涡管

同流线一样，在涡量场中，也有反映同一瞬时流体各质点涡量方向的曲线——称为涡线。在给定的瞬时，涡线上各点的涡向量在该点处与涡线相切。

涡线方程（对应流线方程）：

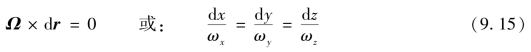
例9．1 当x坐标选在管轴时，管中层流运动的速度分布为

试求涡线微分方程。

解 角速度分量

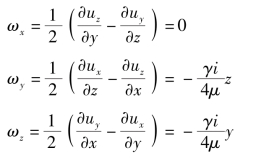
涡线微分方程

(https://www.daowen.com)

代入角速度分量

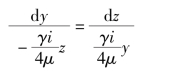
或　ydy＋zdz＝0

积分得 y2＋z2＝C

故涡线是和管轴同轴的同心圆。

在涡量场中任意画一封闭曲线，通过这条曲线上的每一点所作出的涡线构成一管状的曲面，称为涡管。涡管对应流管，若曲线无限小，则称为微元涡管。

（3）涡通量（涡管强度）

设A为涡量场中一开口曲面，微元面dA的外法线单位向量为n，涡量在n方向的投影为Ωn，如图9．3所示。

对于微小的涡管：

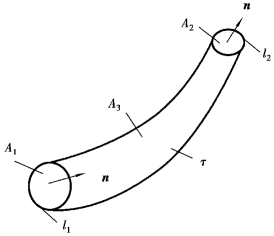
图9．3　Stokes定理

dK＝ΩndA

面积分，得

K称为涡通量或涡管强度。

（4）速度环量

在流场中任取一封闭曲线l（可缩曲线），如图9．4所示，则流速沿曲线l的积分，即

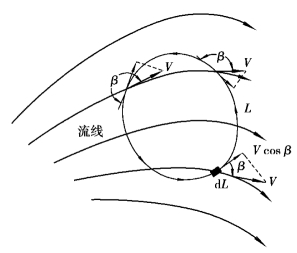
图9．4　速度环量

称为曲线l上的速度环量，并规定积分沿l逆时针方向绕行为l的正方向。

由以上概念可知，对于有旋流动，其流动空间既是速度场，又是涡量场。涡量场中的涡线、涡管、涡通量等概念分别与流速场中的流线、流管、流量等概念相对应，而涡线方程和涡管的涡通量方程则分别与流线方程和连续性方程相对应。