显示二阶网络状态轨迹的实验（2.20）

1）实验目的

（1）观察RLC网络在不同阻尼比ξ值时的状态轨迹。

（2）熟悉状态轨迹与相应瞬态响应性能间的关系。

2）实验设备

（1）TKSS-C型信号与系统实验箱　　　　　一台

（2）YB4340G型双踪示波器一台

（3）EE1642B型函数信号发生器一台

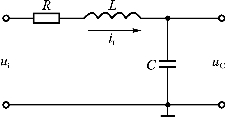
图2.57　RLC电路

3）实验原理

（1）任何变化的物理过程在每一时刻所处的“状态”，都可以概括地用若干个被称为“状态变量”的物理量来描述。例如，一辆汽车可以用它在不同时刻的速度和位移来描述它所处的状态。对于电路或控制系统，同样可以用状态变量来表征。例如图2.57所示的RLC电路，基于电路中有两个储能元件，因此该电路独立的状态变量有两个，如选uC和iL为状态变量，则根据该电路的下列回路方程：

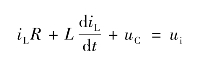
求得相应的状态方程为：

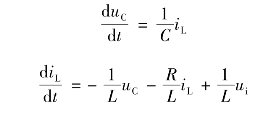
不难看出，当已知电路的激励电压ui和初始条件iL（t0）、uC（t0）时，就可以唯一地确定t≥t0时，该电路的电流iL和电容两端的电压uC。

“状态变量”的定义是能描述系统动态行为的一组相互独立的变量，这组变量的元素称为“状态变量”。由状态变量为分量组成的空间称为状态空间。如果已知t0时刻的初始状态x（t0），在输入量u的作用下，随着时间的推移，状态向量x（t）的端点将连续地变化，从而在状态空间中形成一条轨迹线，叫状态轨迹。一个n阶系统，只能有n个状态变量，不能多也不可少。

为了便于用双踪示波器直接观察到网络的状态轨迹，本实验仅研究二阶网络，它的状态轨迹可在二维状态平面上表示。

（2）不同阻尼比ξ时，二阶网络的相轨迹。

二阶网络标准化形成的微分方程为：

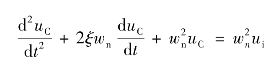
可推得：(https://www.daowen.com)

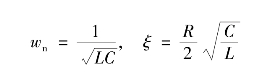
由上式可知，改变R、L和C，使电路分别处于ξ＞1、0＜ξ＜1和ξ=0三种状态。根据状态方程可直接解得uC（t）和iL（t）。如果以t为参变量，求出iL=f（uC）的关系，并把这个关系画在uC-iL平面上。显然，后者同样能描述电路的运动情况。图2.58、图2.59和图2.60分别画出了过阻尼、欠阻尼和无阻尼三种情况下，iL（t）、uC（t）与t的曲线以及uC与iL的状态轨迹。

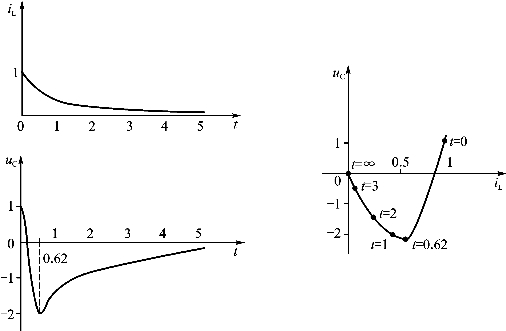
图2.58　RLC电路在ξ＞1（过阻尼）时的状态轨迹

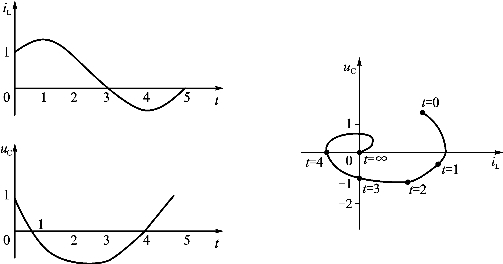
图2.59　RLC电路在0＜ξ＜1（欠阻尼）时的状态轨迹

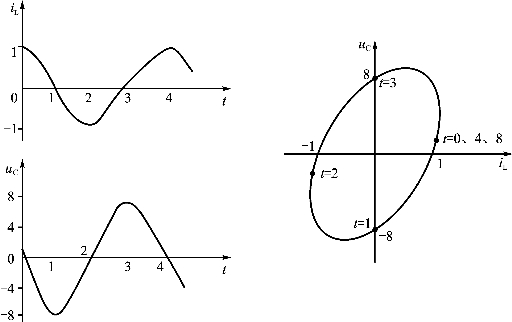
图2.60　RLC电路在ξ=0（无阻尼）时的状态轨迹

实验原理如图2.61所示，uR与iL成正比，只要将uR和uC加到示波器的两个输入端，其李萨如图形即为该电路的状态轨迹。

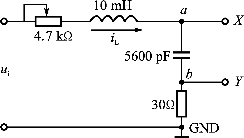
图2.61　实验电路图

4）实验内容

（1）在TKSS-C型信号与系统实验箱中，观察状态轨迹采用了一种简易的方法，如图2.61所示，由于该电路中的电阻值很小，在b点电压仍表现为容性，因此电容两端的电压Ua、Ub分别接至示波器X轴和Y轴，即能显示电路的状态轨迹。

（2）输入1 kHz的方波信号，调节电位器，观察电路在ξ＞1、0＜ξ＜1和ξ=0三种情况下的状态轨迹。

5）预习要求

（1）熟悉用双踪示波器显示李萨如图形的接线方法。

（2）确定所用实验网络的状态变量，在不同电阻值时，状态轨迹的形状是否相同。

6）实验报告

绘制由实验观察到的ξ＞1、0＜ξ＜1和ξ=0三种情况下的状态轨迹，并加以分析、归纳与总结。

7）思考题

（1）为什么状态轨迹能表征系统（网络）瞬态响应的特征？

（2）如何测量电流iL？