【摘要】：因为这种数字滤波器所对应的差分方程是利用差分方程或系统函数可以直接画出递归式滤波器的一般结构，如图2-25所示。+aNy（n—N）可见，递归型数字滤波器当前的输出不仅与当前输入和以前的输入有关，而且还与以前的输出有关。于是递归型数字滤波器的传递函数为在计算机中的计算公式为y=x—x（n—1）+x（n—2）+1.5y（n—1）—0.75y（n—2）若设由逆变换得由式和式可得到简化直接型递归式滤波器的结构，如图2-27所示。
因为这种数字滤波器所对应的差分方程是
利用差分方程（2-81）或系统函数（2-80）可以直接画出递归式滤波器的一般结构，如图2-25所示。
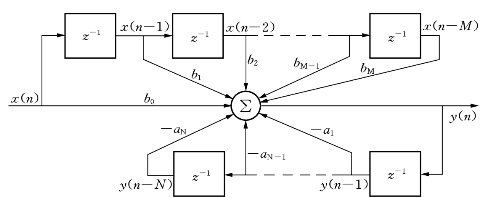
图2-25 递归式滤波器的一般结构图
该差分方程可展开为
y（n）=b0x（n）+b1x（n—1）+…+bMx（n—M）
—a1y（n—1）+a2y（n—2）+…+aNy（n—N）
可见，递归型数字滤波器当前的输出不仅与当前输入和以前的输入有关，而且还与以前的输出有关。
则H1（z）的设计与零点设置有关，而H2（z）则与极点设置有关。下面着重分析一下如何设置极点。首先，极点也必须按共轭成对设置。其次，极点必须设置在单位圆内，即复数的模值必须小于1。
例如想在基波处设置一个极点，则
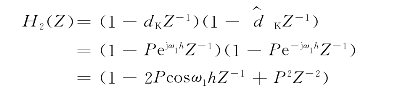
式中 P——极点所对应的模值。
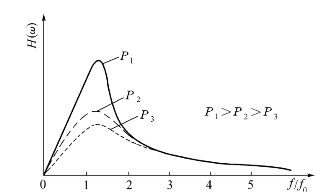
P值选多大呢？一般P越接近于1，在极点频率上滤波器输出值越大，但滤波器达到稳定输出所需的时间越长。如图2-26所示。
(https://www.daowen.com)
图2-26 滤波器达到稳定所需的时间与输出值的关系
为便于处理起见，取P2=0.75，则
，2Pcosωh=1.5（fS=600），于是有
H2（Z）=1—1.5Z—1+0.75Z—2
如果零点设置为二次谐波，10次谐波，则H1（Z）=1—Z—1+Z—2。
于是递归型数字滤波器的传递函数为
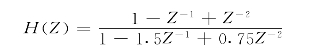
在计算机中的计算公式为
y（n）=x（n）—x（n—1）+x（n—2）
+1.5y（n—1）—0.75y（n—2）
若设
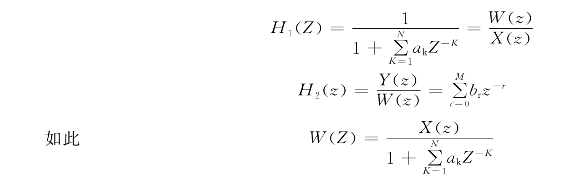
由逆变换得
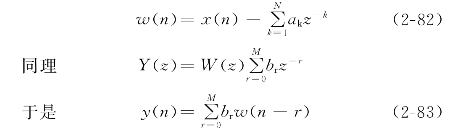
由式（2-82）和式（2-83）可得到简化直接型递归式滤波器的结构，如图2-27所示。
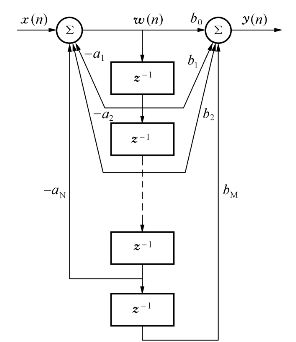
图2-27 简化递归式直接型滤波器结构图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
