无线电信道的建模方法优化

物理信道模型通常基于由无线电传播测量得到（经常是噪声）的参数。除了强烈的由镜像影响造成的多径组成（Multipath Component，MPC）外，无线电工程师（级别）（Institute of Radio Engineer，IRE）的无线信道协会包括在一系列额外延迟上的更低的、发散的“背景”能量，这些延迟相信是电磁散射的结果。除非对这种能量做出贡献的组成部分能从测量中得到准确估计，否则它们既不能正确地用于仿真建模，它们的存在也抑制了来自测量数据的其他参数的估计。Richter和Thoma（见参考文献［TLRT05］）已经阐明了对这种估计问题的解决办法。

基于物理观点，他们推测在一个测量系统延迟解决间隔内和背景能量联系的IRE组成（电压）可以建模成复杂的均值为零的圆正态分布（在随机的选择中）模型。它们的相位适度地建模成在（-π，+π）间均匀分布。在连续统一的延时上的一系列元件建模成一个StP，功率按延时函数呈指数衰减，开始于一个RX处和最早到达能量有关的起始延时。为了完成一个StP建模的所需组成，必须描述不同延时上的散射能量的组成间的协方差。由于这受到测量系统带宽的影响，一个对所需协方差的频域描述在同样的频率间隔里被测量系统寻呼谱的协方差复用，且结果转换回延时域。然后，完整认识了上述描述的用于背景成分的随机模型，一个统计值就可以从（频域）信道转移函数的抽样版本中得到。

基于描述发散背景能量的StP服从高斯分布的这样一种推测，抽样的数据建模成多变量的圆形高斯分布d_bStP～N_C（0，R（θ））。给定参数模型的矢量θ，写出了用于背景StP的（测量的）实现的概率密度函数和它的对数似然函数。这些表达随后扩展为采用一个IRE的测量时间系列。一个用于相应（频域）协方差矩阵的抽样版本公式也可以写成:

R_f（θ）=toep（κ（θ，κ（θ）^H） （6.1）

其中，

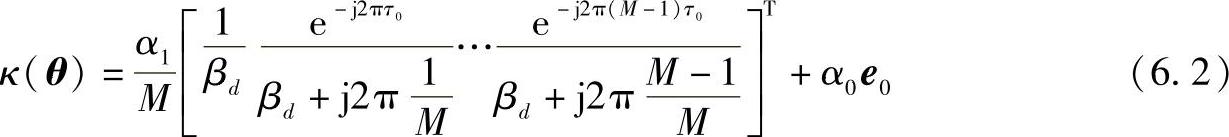
式中，α₁是τ=τ_d时发散成分的功率;M是在测量带宽内测量的频率点的数量;β_d是发散成分的连贯带宽，归一化到测量系统的带宽;α₀是圆形独立同分布常规测量噪声的方差，而e⁰=［1，0，…，0］^T是一个单位矢量。

为了完成建模，涉及镜像元作为背景（散射的）元分配的本地平均值，且这些平均值的对数似然函数的最大值作为加权最小均方问题处理。作者预示发散背景和镜像元的联合估计可以纳入恰当的高分辨率参数估计算法（像ESPRIT、SAGE和RIMAX），来显著提高参数估计准确性。例如，他们建议在使用SAGE或者RIMAX的时候，联合最优化可以被镜像和发散模型在连续步骤内的最优化问题之间的简单转换所影响。

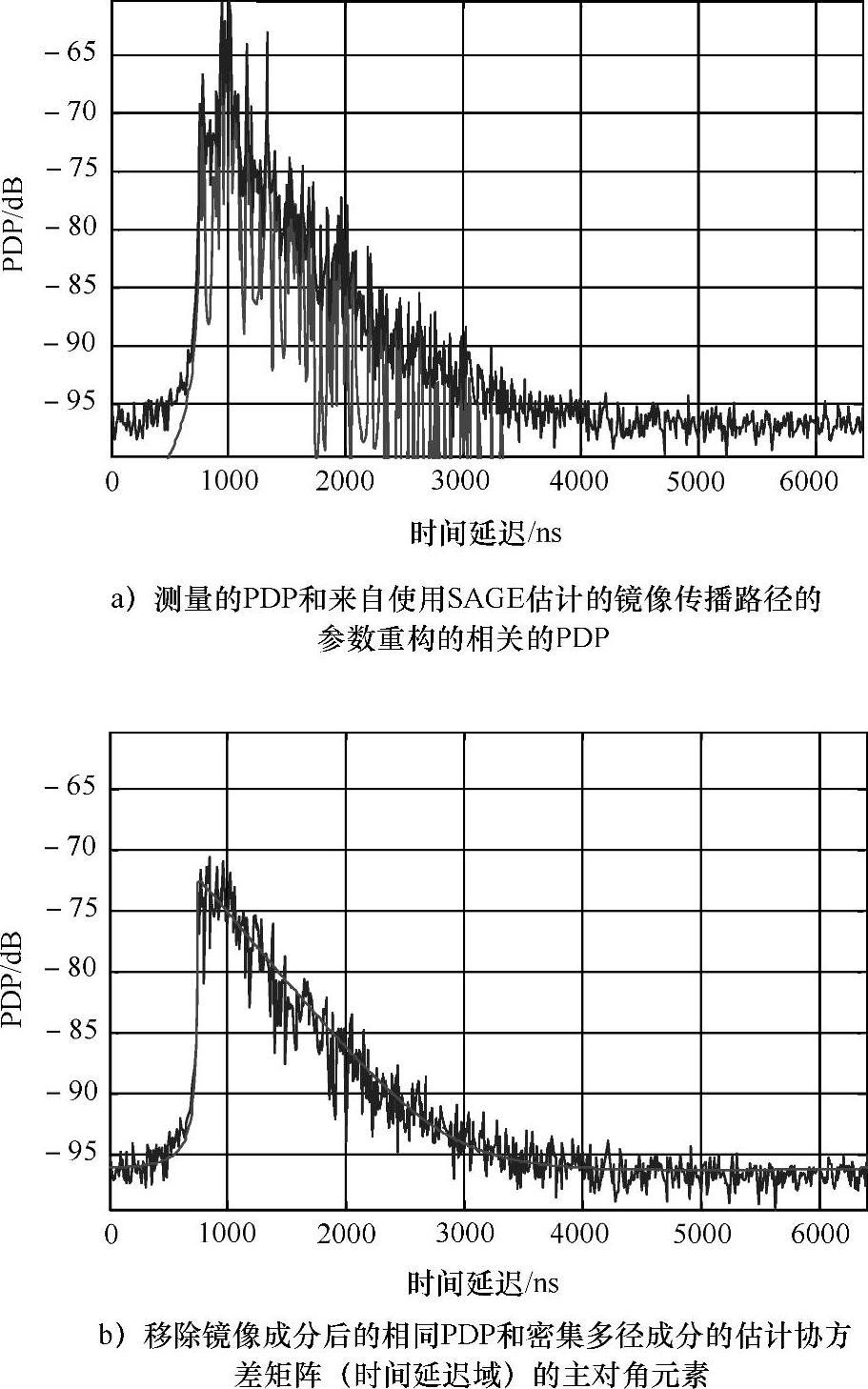
图6.7 测量PDP中的镜像和漫反射内容估计的结果

图6.7显示了来自一个在街道微蜂窝内测量的镜像和发散成分的联合估计结果，该街道微蜂窝测量使用由一个在RX基站的8个成员线性阵列和一个在TX的全方向天线配置的RUSK信道探测器组成。该图清晰地显示了在用于信道参数建模的测量数据的分析中、报告方法的优势。本节的剩下部分报告了COST 273参与者在发展和执行CP模型上进行的工作，该模型基于一些包含在TX和RX之间无线波传播的机制的伪物理（或者近似）建模^[5]，通常使用来自测量的信道参数估计。在一个实际的移动无线信道中，无线电波可以经受来自在CrR的IO的多散射、衍射以及发射。然而，一个假伪理模型可能被基于以下考虑而发展，例如，只有来自IO的镜像反射有反映MT和BS间位置的测量传播延时的几何条件，镜像反射是否是真正的造成来自涉及到IO再发射的原理。

Xu（见参考文献［XCHV02］）发展了一个基于普通类几何的建模方式，并通过和纽约市记录的室外宏蜂窝传播测量的分析比较进行测试。报告的建模方式是宽带信道实现通过使用任何给定的信道统计集合来进行仿真，包括即时PDP，TX和RX处的方位光谱，以及预期的天线阵列配置。基于假设一个MLk矩阵H的每个成员都是来自L个波能量的叠加结果，对应于在延迟“q”的MT天线成员“n”和基站天线成员“m”的H的成员，和时间步骤“s”根据以下产生

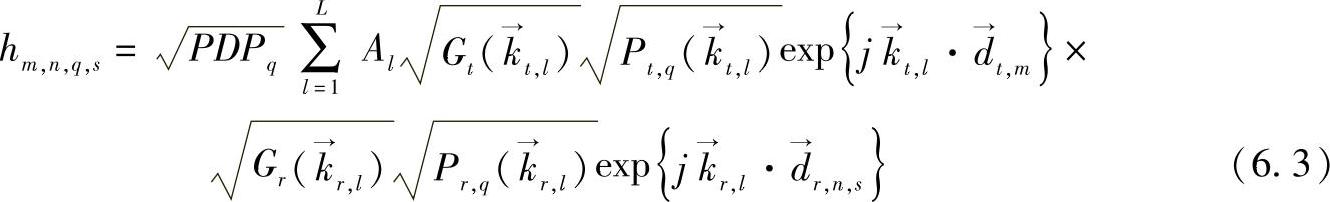
式中，A_l是一个复杂的高斯变量，A_l=x+jy，且x，y～N（0，1）;G_t，G_r分别是TX和RX天线的增益;k=2π/λ;P_t，q是作为DoDs函数的功率方位分布（PAS）;P_r，q表示作为DoA的函数的PA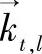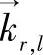，，分别表示在第l个平面波的DoD和DoA到TX和RX的方向矢量。

第m个接收天线成员的位置独立于时间，且表示为→d_m。第n个天线成员的位置是时间步骤s和它的速度的函数，且由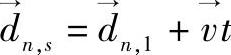给出。通过传播媒介的相位偏移由Al的相位建模，A_l是在［0，2π］均匀分布的。如果要求包括一个LoS组成来产生有着给定莱斯因子K的衰落，将根据以下加入一个强平面波

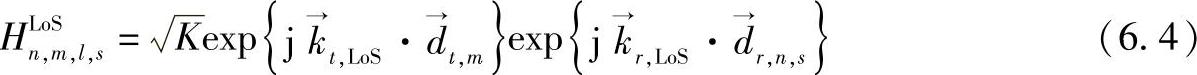
本文也给出了一个从前述的链路级模型扩展到解决多用户和多基站的系统级模型的方法。

参考文献［XCHV02］中的模型验证结果包括对类型Ⅰ在仿真中相应于35°的MT-PAS宽带与10km/h的车速环境下得出的相关数据。对于小间隔（即小天线成员间隔）的情况，预期理论相关函数和由克拉克的模型得到的函数显示有着很好的一致性，诸如那些适合考虑MIMO天线的情况。容量CDF的比较也同样地好，且介绍了可以预料到的和瑞利独立同分布环境相关的退化。对使用测量数据估计的参数模型仿真得出的容量CDF和使用用于4×MLk的测量数据直接获得的那些进行比较，在引证工作中显示了建模和基于测量的结果间的一致性是极好的。

Oestges等人（见参考文献［OeEP04］）提出了一个双极性、几何基础上的信道模型，用于2.5GHz上的固定本地多点分布系统类型链路。首先使用它的是PDP的规范，这一规范是对特定的在BS、系统带宽和天线模式以及极化特性范围内有效。随后通过将IO放置成椭圆形且尺寸与PDP内的多径组（Multipath Group，MPG）的延迟相关，指定了一个物理操作环境以匹配PDP。假设一个抽头延迟线性类型索引的抽头延迟线性模型用于信道脉冲响应，且每个抽头被分配一个时间平均的功率、延迟以及服从一个有特定莱斯因子的莱斯衰落分布。

每个IO能量的极化特性通过在参考文献［Oest02］定义的系数矩阵来定义，参考文献［Oest02］包括了对数正态分布随机变量，有着衰减的正交和交叉极化耦合分子和同极化耦合分子的相位偏移复制。尤其需要注意同极化和异极化间增益不平衡的合并。天线XPD特性也在一个特定延迟MPG上接受到的能量的最终分配上得以说明。除了来自非相干散射的能量外，可以建模由一个LoS分子和相干散射因子的总和组成的相干能量。最后，使用重联合过程合入多普勒特性，在这个过程中，考虑的IO的数量的一部分在每个离散仿真时间间隙Δt内被移除。在每个重联合中被移除的IO数量是一个泊松随机变量ζ，其均值由E［ζ］=1-exp（-nΔt）给出，其中n和所需的多普勒扩展有关。

参考文献［OeEP04］报告了涉及2×2MLk的仿真，每个天线阵列有一个垂直极化和一个水平极化天线元。有3个MPG的PDF使用一个三抽头的、抽头延迟线性模型，该模型有着用于离基站7km范围内的典型瑞利以及莱斯衰落信道的IEEE 802.16推荐相关的性质。正如在引用的文章中提到的，其他范围内的PDF是基于这个参考轮廓散射来进行仿真的。各态历经容量使用类型Ⅱ的时间平均来计算，以取代对不同基站用户范围、天线极化以及XPD联合的期望。结果表明延迟扩展信道容量只是微弱地取决于传输范围，即使是瞬时RMS，衰落特性以及交叉极化分离范围影响非常明显。

Molisch（见参考文献［Moli04b］）提出了一个用于宏蜂窝移动无线环境中MIMO信道的一般模型。这一模型充分地基于COST 259定向信道模型（见参考文献［MAH-Sed］），并做了个重要的扩展。这包含常被指为双散射相关的建模，即使物理原理不需要限制在电磁散射。参考文献［MAHS05b］讨论了单散射模型，允许以下可能:

1）从BS到MT的能量的直接传送。

2）从位于接近MT（通常环绕在MT的周围）的IO上的BS发射能量的入射，并随后重发射到MT。

3）从位于远离MT（通常环绕在MT的周围）的IO上的BS发射的能量的入射，并随后重发射到BS。

4）MT和BS间的对相互传播路径的相似的相互作用。(https://www.daowen.com)

假设从多IO到RX终端的能量传输导致了多MPC的接收，这说明了在这种模型里有主要的、强镜面反射的情况。称为“双散射”的扩展包括了这样一种可能性:来自基站的能量首先是在临近基站的IO上的事件，随后再辐射，直接在MT接收或者通过临近MT的IO接收。不认为通过涉及远程（指“远”）IO的双（即两个连续的）相互影响的能量接收是接收能量很微弱的可能性的结果。

Molisch突出了在“双向”和“矢量（矩阵）”信道建模间的差别，但是强调虽然方法不同，结果却必须是确定的。双向建模时基于物理考虑，并产生了遵照每个MPC下的传播路径的脉冲响应的估计。这些估计的单径脉冲响应函数的总和随后被用作信道（即一个无线链路）的脉冲响应模型。由于脉冲响应的结果包括DoS、DoA、延迟以及所有MPC幅度的信息，一个MLk矩阵可以容易地得到计算。使用双向测量结果的一个优点是这些参数可以几乎独立于测量设备特性得到。Molosh的一般模型在COST 273行动中得到持续修正。细节将在6.8节进行讨论。

Hoffstetter和Steinböck在模型实现中采用了Molish的方法，且结果记录在参考文献［HoSt04］中。假设一个或一些BS，以及远IO和在BS和MT（随着它移动）附近的IO，作为一个MT速度的矢量。在每个IO，假设镜面反射，且一个射线追踪工具计算按照MPC的路径联系的脉冲响应函数。完整的信道脉冲响应函数以及MLk矩阵随后会像在参考文献［Moli04b］中描述的那样进行仿真。（软件）的实现包括传输调制（Propa-gation Module，PrM），一个天线调制（Antenna Module，AnM）以及一个卷积调制（Convolution Module，CoM），并在PrM和AnM以及AnM和CoM间有合适的端口。合成的双向信道信息（包括在波形极化上的专断的随机信息）在PrM里产生并用于AnM，它说明了天线对不同极化的反应，且对于每个MPC以一个衰减和相位偏移的形式中的后者出现。这些结果随后在CoM中总结来形成信道脉冲响应以及MLk矩阵。长期的功率变化在MLk矩阵成员的标准化中得到说明，且作为类型Ⅰ、Ⅱ和Ⅲ随机变化的结果的真实衰落相关性在MIMO分析中进行估计。仿真的MLk的容量在图6.8中显示，且显著地低于那些在独立同分布瑞利衰落情况下达到的容量。

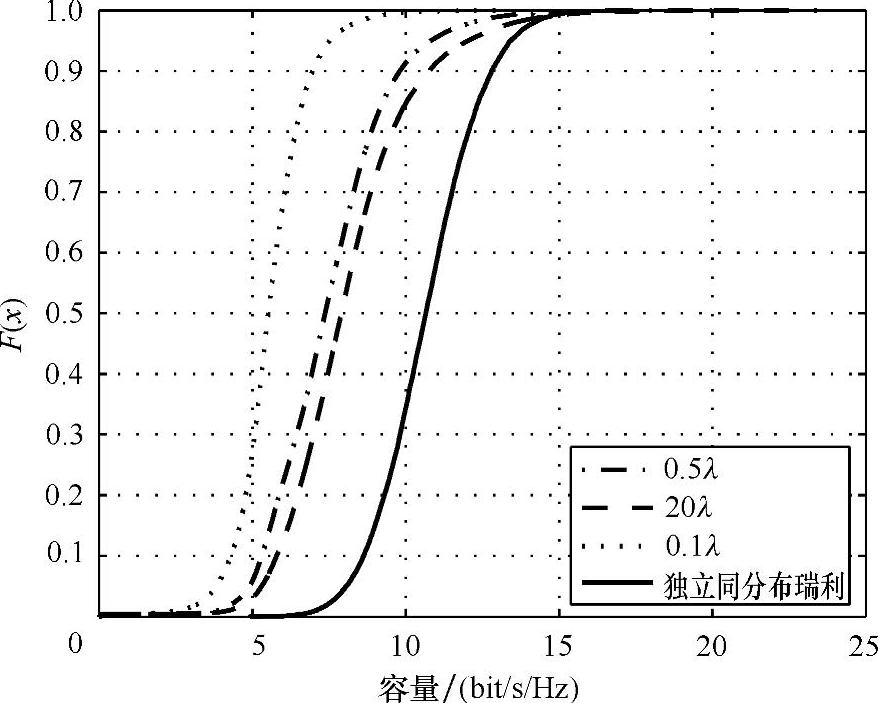
图6.8 选择的天线元间隔的中断容量

图中也显示了不同天线成员间隔的容量变化，也说明了容量随着仿真中考虑的IO数量变化而改变。

对系统级的MIMO系统的研究，需要一个准确的空间色散的蜂窝内及蜂窝间干扰的描述。这意味着为了增加临近MLk间的距离，信道参数的自相关也应该增加。这点在绝大部分物理基础上的MIMO信道模型中不予考虑。然而，参考文献［FKMW04］中给出的多用户双向信道模型（Multiuser Double-Directional Channel Model，MDDCM），使得能够准确描述在宏蜂窝环境（见参考文献［FKMW04］）下的干扰。模型的概念性基础类似于和基于几何的随机信道模型相关的那些，但是与之相反的，和IO相关的位置和参数在每个信道实现中重复地被随机计算。传播环境产生于前段处理过程并在整个仿真过程中保持固定。

报告的MDDCM涉及新的用于MT周围和IO相互影响的新模型，以及用于沿着高楼中间的街道的传播。参考文献［AMSM02］，［Moli02］包括用于远集群和可视通路场景的已知模型。本地集群建模如图6.9所示。为了简化，图中只显示了2维平面。固定的IO均匀地分布在整个3D仿真环境中，该环境可能覆盖一些BS和MT。每个MT位于一个圆/椭圆柱体上，定义了本地集群。由于只有在柱体内的IO是活跃的，这种柱体就用作搜索函数。IO建模为理想的、完美导向的矩形盘。根据参考文献［Svan01］得到的模型，来计算经历MT和基站间单一相互作用的射线。这种模型的优点是解释了基础时空性质（例如，入射波场的解极化，“散射”叶）。

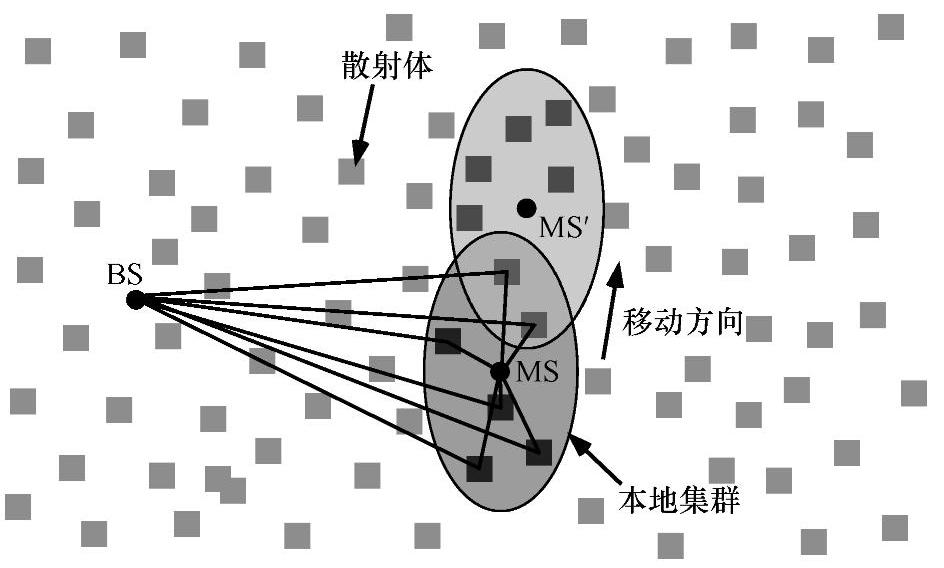
图6.9 建模本地集群的方法

为了说明时间变化信道行为，把信道模型和移动模型联系在一起。当MT移动到一个新位置，许多新IO就贡献能量给接收信号，同时来自旧IO的一些能量减弱。作为一个仿真模型，使用在参考文献［ETSI98］中定义的近似曼哈顿移动模型。城市环境的街道网格建模成一个“棋板”。移动站沿着街道线性地移动且可以在每个十字路口改变它们的方向。根据MT的位置，对本地集群的形状和大小进行调整。如果MT位于高楼中间的街道处，本地集群就建模成一个椭圆柱体。如果MT位于十字路口，本地集群则为圆柱形状。

在宏蜂窝环境下，一些波形从BS传播到十字路口。然后，由于高楼中间的街道效应，这些波被引导到MT。它们的DoS（方位与仰角）以及它们的延迟高度相关。高楼中间的街道造成了跟波导一样的现象。为了建模沿着高楼中间的街道的传播，假设所有建筑位于沿着近似曼哈顿街的网格上，因此这种网格体现了一种波导结构。除了波导，还需要建模十字路口附近的波形交感点。为了这个，在每个临近十字路口的圆柱体上放置额外的IO，射线从BS传播到MT。使用高楼中间的［FMKW04］讨论的3D图像理论，可以计算关联的传播参数，图6.10给出例证。

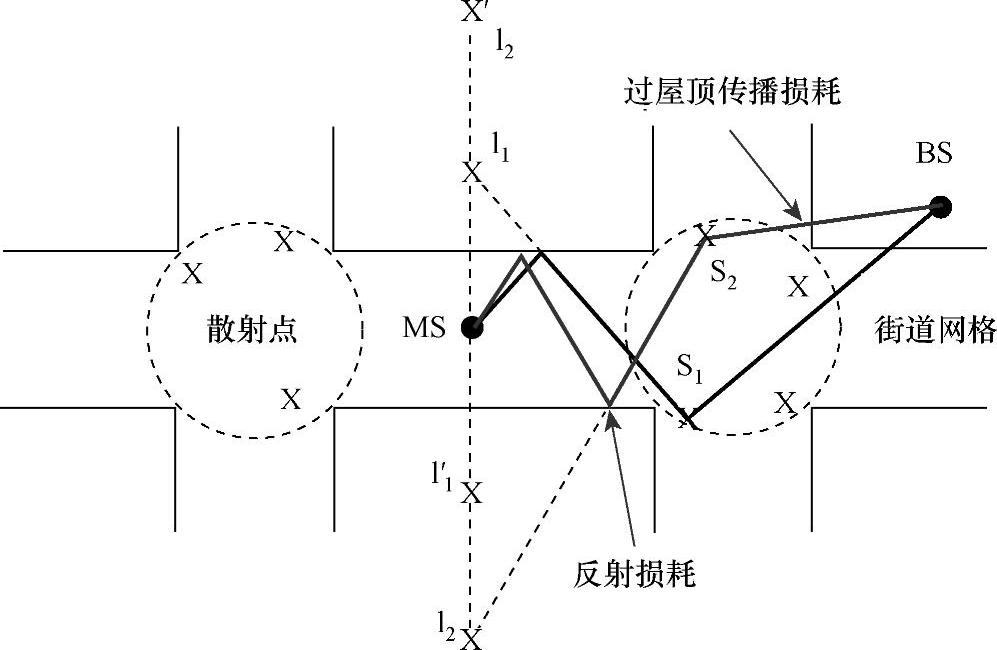
图6.10 和街道导向相关的镜像原理

Sibille（见参考文献［Sibi01］）给出了所谓锁眼信道的物理模型概念，它是基于冲击到一个锁眼的输入波和许多由衍射现象产生的输出波之间结合的考虑制定了一个建模方法。信道转移函数矩阵以TX和RX阵列的指导矩阵和一个描述两个阵列上复杂波幅度间相互关联的“连接”矩阵来表达。由将入射波分裂成多输出波导致的连接矩阵的非对角特性，当该矩阵有多半非零实体（即，当它是满矩阵的时候）时，将造成一个锁眼。本文给出了一个不同的完全吸收平面内，时隙的任何一侧都有TX和RX阵列的3×3MLk的例子。对4种涉及不同阵列成员间隔和两个不同时隙宽度的不同情况进行了容量CDF的估计。对于相应于微不足道的衍射的一个很宽的时隙（5λ），以及相对应于阵列上类型Ⅳ随机变量的小空间相关性的大阵列（1λ）成员间隔，容量估计为3.54bit/s/Hz。然而，当时隙宽度减少到1/4λ时，容量估计就减少到2.5bit/s/Hz。伴随着狭窄的时隙，进一步表明在每个阵列将天线间隔减小到1/10λ以增加空间相关性对容量没有影响。这表明MLk已经减少，通过狭小时隙和随之而来的衍射效应来换取单自由度。可以发现，当时隙宽从大约两个波长减少到约一个波长时容量的增加最多。

参考文献［Sibi01］发展了用于MLk矩阵的频域描述和它的相对应的延迟域的公式，假设了M个发射波结合在一起变成N个接收波。频域表达式如下:

H（w）=A_r（w）W（w）A_t^T（w） （6.5）

式中，A_r和A_t代表阵列指导矩阵;而W是波形连接矩阵。

在简单的衍射时隙的3×3例子中，该矩阵将有以下成员

w_ij=R_ij^Tij^Kije^-jklie^-jklj （6.6）

式中，R_ij和T_ij是在时隙边上的波形衰减，相应应传播长度l_i和l_j;K_ij是和路径ij有关的Kirchhoff衍射系数。

采用傅里叶变换给出

H（τ）=A_r（τ）W（τ）A_t^T（τ） （6.7）

在这一公式中，指导矩阵和耦合矩阵都有取决于在阵列上的相互耦合的狄拉克delta函数的实体，以及TX和RX阵列之间的各种PLk的传播延迟。所有参数都可以从双向信道寻呼测量中得到估计。Sibile推测，在实际场景中的联合矩阵，可能可以通过考虑冲击在RX的组波是明显的有着随机DoS和DoA的瑞利衰落信号，来减小其大小。