均匀线路传输矩阵探究

在工频稳态条件下考察一回均匀对称输电线路，图2-1展示了一条单相线路，该线路的参数取正序模型中的分布参数，即每个无穷小段dx采用4个参数来描述，这4个参数也称为一次参数，即r、l、g和c。对于交叉互连和三相循环换位的电缆线路，这4个参数的计算方法见2.3.1～2.3.4节；对于紧固互连的气体绝缘输电管线（GIL），这4个参数的计算方法见2.4.1～2.4.4节。而对于架空输电线路，这4个参数的计算公式是众所周知的。

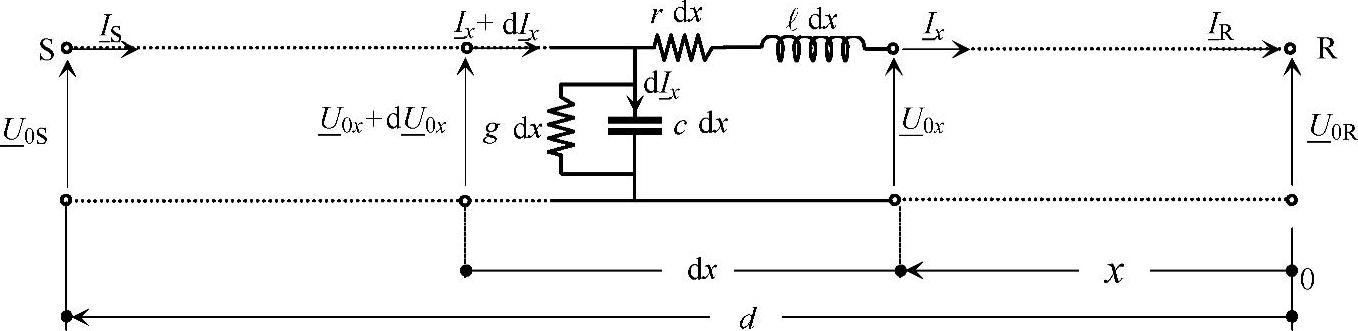
图2-1 一回输电线路的正序单相模型

整条线路的送端和受端以及无穷小段dx上的电压和电流的参考方向如图2-1所示。在稳态条件下，当角频率为ω时，每个无穷小段具有的纵向阻抗和并联导纳为

式中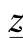，是单位长度纵向阻抗，单位为Ω/km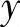；是单位长度并联导纳，单位为S/km。

距受端R x（km）处的无穷小段dx的两个端口之间的电压升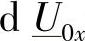等于纵向阻抗zdx上的电压降，因此有

而无穷小段dx的两个端口之间的电流变化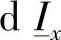等于无穷小段并联导纳中流过的电流，即

考虑到式（2-3）中的高价小量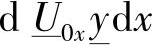可以被忽略掉，式（2-2）和式（2-3）可以被重新写成如下形式：

应当记住，稳态相量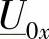和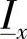是以恒定角频率ω旋转的，它们决定了时域中正弦量的瞬时值（即将相量投射到参考轴上，其值与相量的相位角有关）。这样，剩下的问题就是求解由式（2-4）和式（2-5）构成的微分方程组，且将电流和电压相量看作仅仅是空间变量x的复函数。

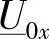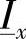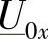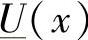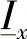通过拉普拉斯（Laplace）变换，将复函数和变换到s域中，设变换后为，变换后为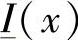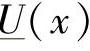，和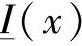为实变量x的函数。根据著名的函数导数变换式

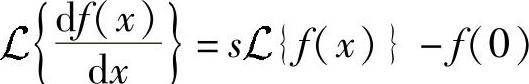
在受端作为坐标原点的情况下，显然有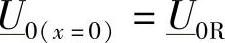和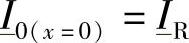，应用上式，可得到如下的方程组：

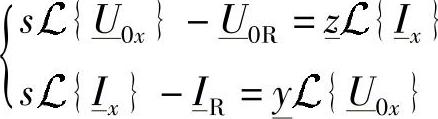
重新整理上式，可得

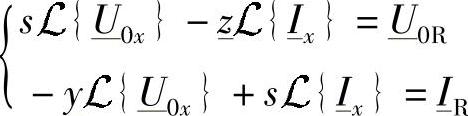
求解上述方程（根据Cramer法则），立即可以得到

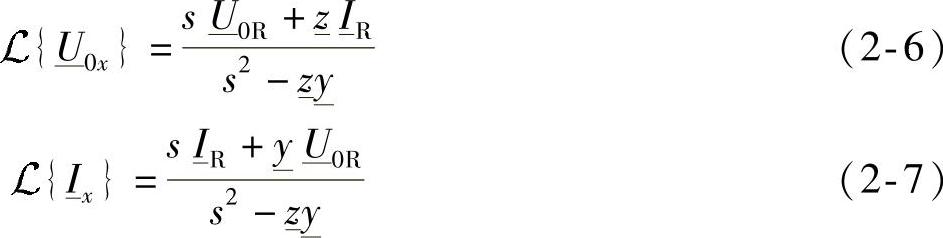
如果定义新的变量和为

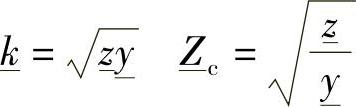
则

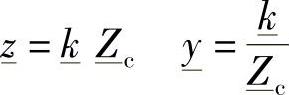
因此可以将式（2-6）和式（2-7）表述成其最终形式，即(https://www.daowen.com)

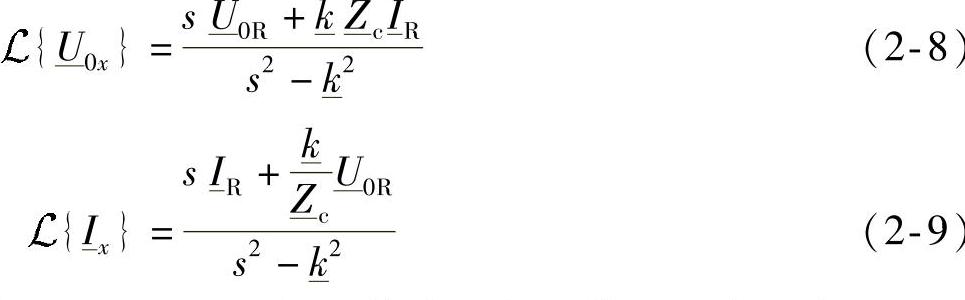
对上两式进行拉普拉斯反变换，电压和电流相量作为x的函数可以表述为

式中

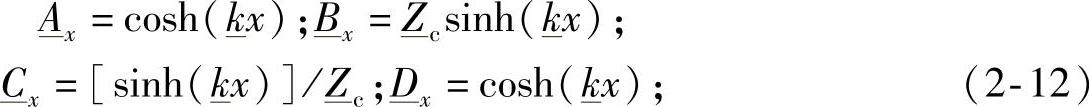
而x是考察点与受端之间的距离，单位为km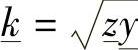；，称为传播因数，单位为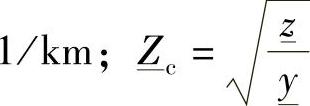，称为特征阻抗或自然阻抗。

如果将双曲函数通过欧拉（Euler-Lambert）公式用指数函数来表示，可以得到传输线公式（电报方程的解）。该公式首先是由O.Heaviside于1876年导出的^[1]，后来又由Arnold^[2]、Roessler^[3]、Steinmetz^[4]等人使用并重新整理过。

如果x=d，可以得到

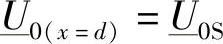
和

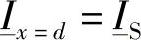
因此，有

式中

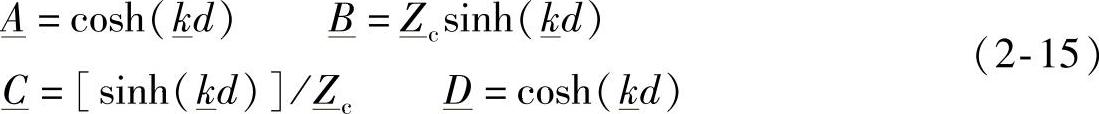
因此，长度为d的线路的单相模型可以看作由参数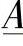、、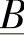、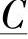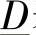表征的一个两端口电路。参数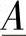、、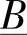、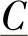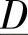也称为传输线的混合参数，因为它们具有不同的单位和不同的电路意义，这在任何电力系统分析的教科书中都是强调的^[5，6]。

由于线路具有均匀分布的参数，该两端口电路是对称的，因此有

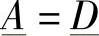
式（2-13）和式（2-14）可以被重新整理成简洁美妙的矩阵形式，即

这里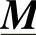，通常被称为传输矩阵。一旦将受端的混合矢量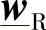固定住，通过式（2-16）就能得到送端的混合矢量。

式（2-16）存在如下的关系：

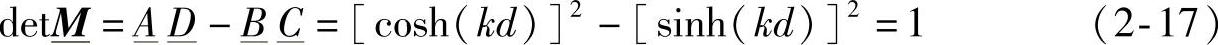
式（2-17）表明，由输电线路构成的两端口电路显然满足互易性原理。