动态电路在初始状态为零的情况下,仅由独立电源作为激励引起的响应,称为零状态响应(Zero-state Response)。初始状态为零意味着在换路前uC(0-)=0和iL(0-)=0,即电路没有初始储能。因此,电路的响应形式,不仅与电路的结构和参数有关,还与外加的激励源有关。本节讨论一阶RC电路和RL电路的零状态响应。
1.RC电路的零状态响应
在图4-15(a)所示的电路中,US为直流电源,开关S在t=0时闭合,闭合前电容上没有电荷,即电容的初始状态为零,闭合后,直流电源对电容充电。根据零状态响应的定义和换路定则有
![]()
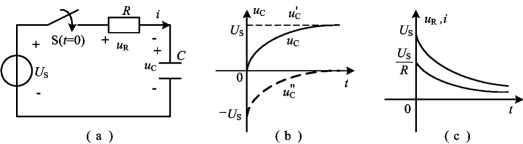
图4-15 RC电路的零状态响应
(a)电路;(b)uc的变化曲线;(c)uR,i的变化曲线
当t≥0+时,由KVL可得
![]()
将电阻和电容元件的伏安关系式uR=Ri和![]() 代入式(4-31)中,得
代入式(4-31)中,得
![]()
式(4-32)为一阶线性常系数非齐次微分方程,该方程的解也可利用高等数学求微分方程的方法确定,为此,可将式(4-32)整理变形为
![]()
对式(4-33)两边积分,并应用初始条件,可得
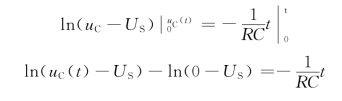
或

用e的指数表示为
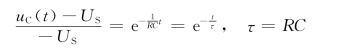
即
![]()
式(4-35)即为电容电压的零状态响应。
回路中电流和电阻电压为
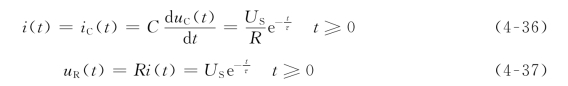
由式(4-35)~式(4-37)可得到电容电压、电容电流和电阻电压的变化规律如图4-15(b)和图4-15(c)所示,显然是呈指数规律变化。
由式(4-35)可见,非齐次微分方程的解由两部分组成,即
![]()
式(4-38)中,u′C=US是非齐次方程的特解,具有与激励相同的形式,所以称之为强制分量(Forced Component)。对于直流、周期激励作用下的RC电路,换路后电路经过一段时间可以达到新的稳态。u′C也就是电容电压在电路重新达到稳态时的值。故又称之为稳态分量(Steady State Component)。![]() 为对应齐次方程的通解,其中的积分常数由初始条件来确定。通解的变化规律取决于电路的结构和参数,它按指数规律衰减到零,故称之为暂态分量(Transient Component),也称之为自由分量(Free Component)。电路过渡过程的特点主要反映在自由分量上,电路过渡过程的快慢取决于自由分量的衰减快慢。暂态分量的形式与激励的形式无关,而暂态分量中的积分常数A由激励初始值决定。
为对应齐次方程的通解,其中的积分常数由初始条件来确定。通解的变化规律取决于电路的结构和参数,它按指数规律衰减到零,故称之为暂态分量(Transient Component),也称之为自由分量(Free Component)。电路过渡过程的特点主要反映在自由分量上,电路过渡过程的快慢取决于自由分量的衰减快慢。暂态分量的形式与激励的形式无关,而暂态分量中的积分常数A由激励初始值决定。
从能量的角度来分析,RC电路的零状态响应实际上是电源给电容充电的过程(Charging Process)。电路中的电阻起到限流作用,若电阻值过小就会导致充电电流初始值过大而损坏电容,过大则会导致充电电流初始值过小而充电时间过长。换路之前,电容没有储存电场能量,在换路后,电源通过电阻给电容充电,将电能转换为电场能量,电容储存的电场能量为

而充电过程中电阻消耗的能量为
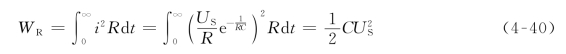
比较式(4-39)和式(4-40)可以看出,电阻消耗的能量正好与电容储存的能量相等。
例4-9 电路如图4-16所示,t<0时开关S打开,电路已处于稳态。在t=0时刻闭合开关S,求t>0时的i(t)。
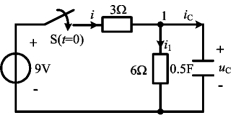
图4-16 例4-9图
解 t<0时,电路已处于稳态,电容相当断开,故有uC(0-)=0。t=0时刻闭合开关S,由换路定则有
uC(0+)=uC(0-)=0
对节点1应用KCL有
i=i1+iC
将![]() ,
,![]() ,
,![]() 等式代入上式有
等式代入上式有
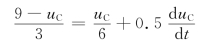
整理得
![]()
可见该方程为一阶常系数微分方程。设该方程的特解为u′C=K,代入微分方程中可求得
u′C=6V
对应齐次方程的通解为
u″C=Aept
将通解代入对应齐次方程中,消去因子Aept,便得到微分方程的特征方程为
p+1=0
所以特征根为p=-1。
则所求齐次微分方程的通解为
u″C=Ae-t
微分方程的解为
uC=u′C+u″C=6+Ae-t t≥0
利用初始条件,得
0=6+Ae0, A=-6
所以有
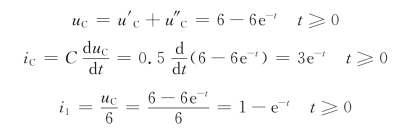
故得
i=i1+iC=1+2e-t t≥0
例4-10 电路如图4-17(a)所示,求零状态响应u0(t)。
解 图4-17(a)所示电路中a、b两点的左边是一个含受控源电路,可以用一个戴维南等效电路代替,如图4-17(d)所示,因此,可将其化为一个一阶RC电路问题。
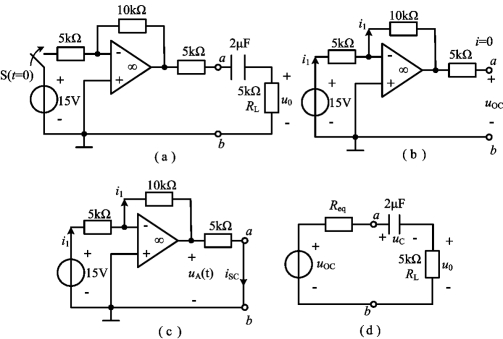
图4-17 例4-10图
(1)根据图4-17(b)所示电路求端口a、b的开路电压uoc(t)。
![]()
uoc(t)=-10×103i1=-10×103×3×10-3=-30V(https://www.daowen.com)
(2)根据图4-17(c)所示电路求端口a、b的短路电流isc(t)。
uA(t)=-10×103i1=-10×103×3×10-3=-30V
故得
![]()
(3)端口a、b的短路输入电阻Req。
![]()
(4)由此可作出等效电路如图4-17(d)所示。将KVL应用于该电路,并利用电路元件的伏安关系,可得
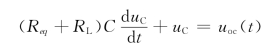
即
![]()
此为常系数微分方程,其解为
uC=-30+30e-50tV, t≥0
![]()
u0(t)=RLiC=5×103×(-6×10-3)e-50t=-30e-50tV, t≥0
2.RL电路的零状态响应
图4-18(a)所示电路中,开关S在t=0时闭合。闭合前,电感上无初始储能,电路处于零状态。
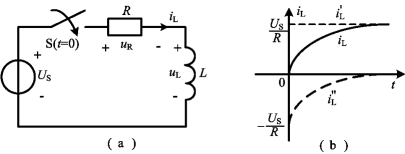
图4-18 RL电路的零状态响应
(a)电路;(b)电感电流变化曲线
当t≥0后,由KVL可得
![]()
将元件的伏安关系uR=RiL,![]() 代入式(4-41),得
代入式(4-41),得

式(4-42)为一阶常系数线性非齐次微分方程。类似RC电路的讨论,该方程的通解由两部分组成
![]()
式(4-43)中i′L是非齐次方程的特解,i″L是对应齐次方程的通解。
非齐次方程的特解i′L应满足

可以求出特解为
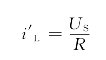
齐次方程的通解为
![]()
所以,方程(4-42)式的通解为
![]()
其中,积分常数A由初始条件决定。由于换路前iL(0-)=0,根据换路定则,有
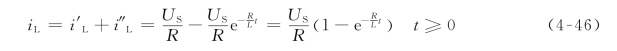
故电感电流的零状态响应为
![]()
式(4-46)所表示的电感电流变化规律如图4-18(b)所示。
例4-11 电路如图4-19(a)所示,t=0时,开关S打开,求t>0后iL,uL的变化规律。
解 这是RL电路零状态响应问题,先化简电路,得到图4-17(b)所示电路,其等效电阻为
Req=80+200∥300=200Ω
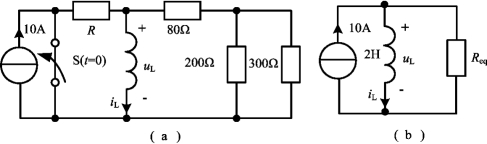
图4-19 例4-11图
由图4-17(b)所示的电路可得
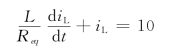
τ=L/Req=2/200=0.01s
电路换路后经过足够长的时间,电路又达到新的稳态,其稳态值为iL(∞)=10A。
所以,t>0后iL,uL的变化规律为
iL(t)=10(1-e-100t)A
uL(t)=10×Reqe-100t=2000e-100tV
例4-12 如图4-20(a)所示电路中,电感未储能。当t=0时,开关S闭合,求iL(t)和i(t)。
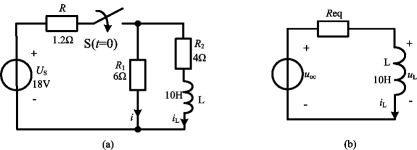
图4-20 例4-12图
解 开关闭合后电路的等效电路如图4-20(b)所示,等效电压源的电压为
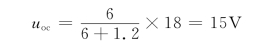
等效电阻为
Req=1.2∥6+4=5Ω
电路的时间常数为
![]()
所以,电感电流的零状态响应为
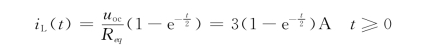
电感电压为
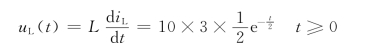
电阻R1两端电压和电流分别为
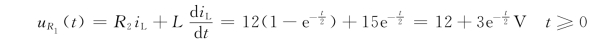
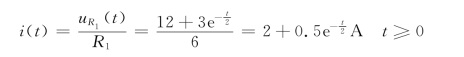
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







