基于分形分布的VaR确定方法优化

风险价值（VaR）的定义：

P（r＜VaRc）＝1-c

式中，r为金融资产在持有期内的回报；c为置信度。

上式表明，在一定的持有期内资产的回报率低于VaRc的概率为1-c。

在给定的置信水平c∈（0，1）条件下，金融资产收益率r在水平c下的VaR定义为：

这里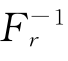，（x）是r的累积分布函数Fr＝P（r≤x）的广义逆函数。

若f（r）为收益率r的概率密度函数，则无论作为收益率r服从什么分布，在给定的置信度c下，下式都成立，即

如果收益率r～N（μ，σ2）的持有期为1天，则(https://www.daowen.com)

由风险价值VaR的定义可以得到：

则基于正态分布的VaR计算公式为：

由于大量的实证研究表明，金融资产收益率的特征参数为0≤α≤2，此时方差不确定或为无穷，因而，样本方差已经不再适合用来度量金融资产的波动性。

设收益率r～Sα，β（γ，δ），则设置信水平为c，根据风险价值（VaR）的定义并结合标准分形分布的性质可以得到：

由此，基于分形分布的风险价值（VaR）计算公式为：

这里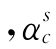代表c置信水平时的分形分布的分位数，其余字母含义与前面的相同。由式（4-10）可知，在分形分布条件下，用尺度的调准参数γ度量金融资产波动性。