海水受到月球和太阳的吸引力作用,产生周期性的升降运动,这种海面升降现象称为海洋潮汐,简称潮汐(陈宗镛等,1979)。太空中的其他星体也对地球产生引力作用,但其对地球变形的影响可以忽略。除了潮汐,海流、风暴潮、江河径流等也都会引起水位变化,由于海洋范围广阔,本节将着重介绍潮汐引起的水位变化规律。
1.潮汐现象
从某一基准面量至海面的高度,称为潮高。为了介绍潮汐现象,我们先了解一些术语。
月中天:月球经过某地子午圈的时刻,称为月中天(或太阴中天),其中,月球每天经过子午圈两次,离观测者天顶较近的一次称为月上中天,离天顶较远的一次称为月下中天。
涨潮和落潮:海面从低潮上升到高潮的过程中,海面逐渐上升,称为涨潮。自高潮至低潮的过程中,海面逐渐下降,称为落潮。
高潮和低潮:在海面升降的每一个周期中,海面上涨到不能再升高时,称为高潮或满潮;海面下降到不能再下降时,称为低潮或干潮。
平潮和停潮:当海面达到高潮的时候,在一段时间内海面暂时停止上升,海面处于暂时平衡状态,称为平潮。当海面达到低潮时候,在一段时间内海面暂时停止下降,海面处于暂时平衡状态,称为停潮。一般取平潮(停潮)的中间时刻为高潮时(低潮时)。
潮差、周期:两个相邻的高潮和低潮的水位高度差,称为潮差。取一段时间内潮差的平均值叫平均潮差。两个相邻高潮或两个相邻低潮之间的时间间隔,称为周期。
涨潮时间和落潮时间:从低潮时刻至高潮时刻所经过的时间间隔,称为涨潮时间;从高潮时刻至低潮时刻所经过的时间间隔,称为落潮时间。
高(低)潮间隙:潮汐主要是由月球引力产生的,而月中天时刻应该是高潮时,但因海水的惰性、海底地形变化以及海岸地形等因素,造成某地月中天时刻未到达高潮,总要经过一段时间,才发生高潮。从月中天至高(低)潮时的时间间隔,叫做高(低)潮间隙。
日潮不等:一日内两次高潮或低潮潮高不等的现象,称为日潮不等,其中,一日内较高的一次高潮叫高高潮,较低的一次高潮叫低高潮,较低的一次低潮叫低低潮,较高的一次低潮叫高低潮。日潮不等是由月球赤纬的变化引起的,月球赤纬是指月球、地球中心连线与地球赤道面之间的夹角。
分点潮和回归潮:当月球在赤道附近,则两高潮(低潮)的潮高约相等,这时候的潮汐称为分点潮。当月球在最北或最南(赤纬最大)附近时,所产生的日潮不等为最大,此时潮汐叫回归潮。
大、小潮:通过长时间观测可以发现潮差在一个月内是随着日期变化的,潮差最大这一天的潮汐称为大潮,潮差最小的这一天的潮汐称为小潮。大潮每月发生两次,一般在朔、望后2~3日出现;小潮每月发生两次,一般在上弦、下弦后2~3日出现。
潮龄:从朔望至发生大潮的时间间隔,称为半日潮龄。从月球最大赤纬至发生回归潮的时间间隔,称为日潮龄。由月球近地点到发生最大潮差的时间间隔,称为视差潮龄。
若将一段时间观测得到的海面高度变化展绘到潮高-时间坐标平面上,则可得到潮汐变化曲线(图9-8)。潮汐变化曲线是有规律的,如果我们在海边一固定处验潮较长时间,并绘制潮汐变化曲线,当能发现上述的一些规律。
在实际应用中,一般将日分潮和半日分潮的振幅比作为划分潮汐类型的依据。在我国一般利用下式对潮汐进行分类:

式中,Hi为某分潮i的平均振幅(分潮调和常数)。其中,下标k1为太阳-太阳赤纬全日分潮,O1为太阳主要日分潮,M2为太阳主要半日分潮。
根据F1取值不同将潮汐分为四类:
①正规半日潮(0<F1≤0.5):在一个太阴日内有两个周期,两相邻的高潮或低潮的潮高几乎相等,此类潮汐称为半日潮;
②不正规半日潮(0.5<F1≤2.0):在一个太阴日内有两次高潮和两次低潮,但相邻的高低潮之间的潮差不等,涨落潮时间也不等,且不等是变化的;
③不正规日潮(2.0<F1≤4.0):在一个朔望月内大多数天是不正规半日潮,但有几天会出现一日一次高潮和一次低潮的日潮潮汐类型;
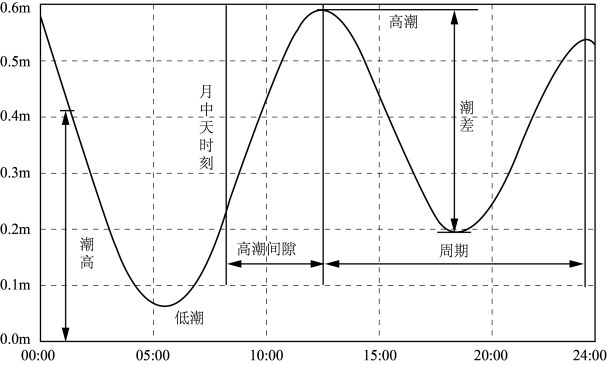
图9-8 潮汐变化曲线图
④正规日潮(F1>4.0):在半个月内大多数天(大于7天)是日潮的性质,少数天发生不正规半日潮。
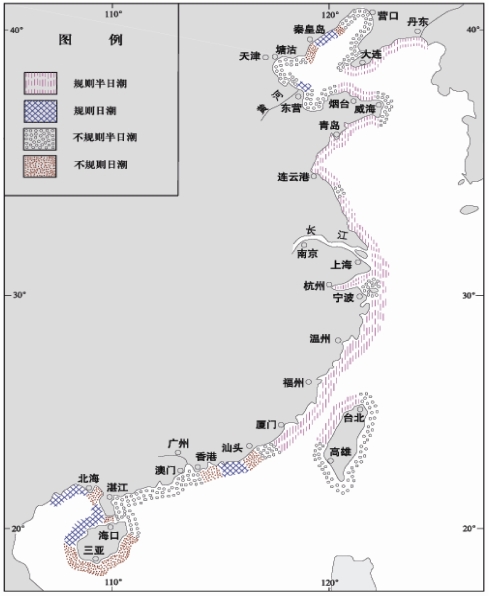
图9-9是四种类型的典型潮汐变化曲线,图9-10是我国沿海港口潮汐性质分布。
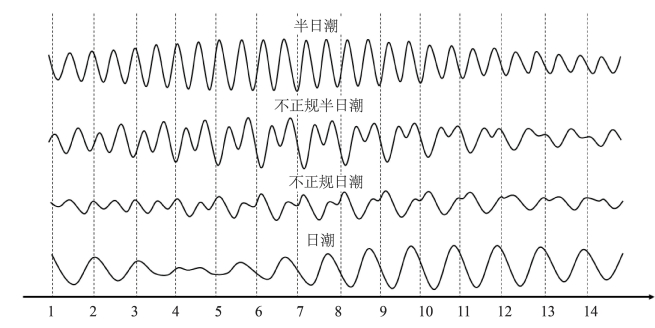
图9-9 不同潮汐类型的水位观测曲线实例
2.引潮力与引潮力势
 (https://www.daowen.com)
(https://www.daowen.com)
图9-10 中国沿海港口潮汐性质分布(吴俊彦等,2008)
海洋潮汐现象主要是月球和太阳的引潮力造成的,尽管太空中其他星体也对地球产生引力作用,但它们要么距离过远、要么质量较小,影响很小,可以忽略。引潮力是指月球和太阳对地球上单位质量的物体的引力与地球绕地月公共质心旋转时所产生的惯性离心力的合力。由于月球是最大的引潮天体,在此将以月球为例解释引潮力和引潮力势,并比较分析月球、太阳引潮力的大小。
如图9-11所示,单位质点A、B、C、D、E在地球各点上受到的惯性离心力FN大小相等方向平行,而月球对地球各点的引力FM因距离的不同而不等。在地心E处,惯性离心力FN与月球的引力FM大小相等、方向相反,合力为零,因而地月之间保持着既不远离又不靠近的平衡状态;而在地球其他各点,由于FM不同,使得FM和FN的合力不为零,此合力即为引潮力。
如图9-12所示,地心E与月球质心M的距离为r,地球某点X至月球质心的距离为ρ,X与地心E之间的距离为R,月球天顶距为θ,E、X延长线与X、M连线的夹角为ψ,G为万有引力常数,则垂直引潮力FV和水平引潮力FH可表示为:
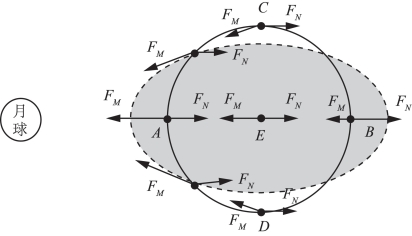
图9-11 地月引力与惯性离心力
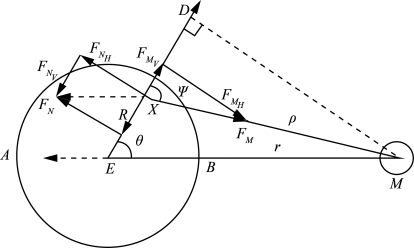
图9-12 月球引潮力分解示意图
![]()
其中,
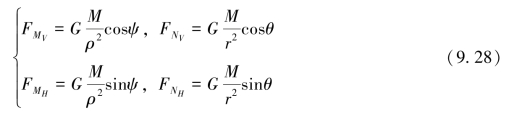
由△EMD和△XMD得:
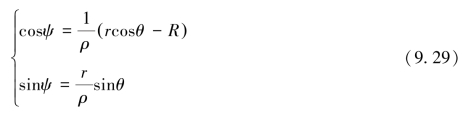
将式(9.28)、式(9.29)代入(9.27),进行泰勒级数展开并省略高阶项得:
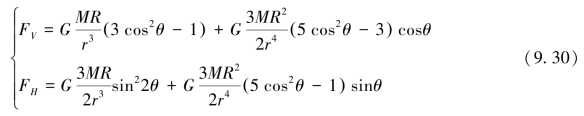
引潮力势是自地心移动单位质量物体克服引潮力所做的功,月球引潮力势表达式为:
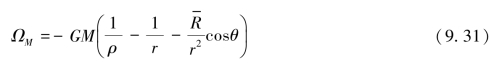
式中,![]() 为地球平均半径。
为地球平均半径。
同理可得到太阳引潮力和引潮力势计算公式,在此不再赘述。表9-2列出了天体基本参数,据此可计算出引潮力数值,通过计算可知:①引潮力量值很小,月球引潮力只是重力的0.56‰~1.12‰,太阳引潮力相比更小;②月球引潮力大约等于太阳引潮力的2.17倍;③月球的最大垂直引潮力大于最大水平引潮力(FH=3FV/4),水平引潮力是引起海面流动和涨落的主要原因。
表9-2 天体基本参数

3.平衡潮理论与潮汐调和分析
17世纪,牛顿用万有引力理论解释海洋潮汐现象,创立了平衡潮理论,又称潮汐静力学理论。理论假设地球表面为等深海水所包围,不考虑海水惯性、黏性、海底摩擦,且忽略地球自转产生的偏向力。通过理论分析,得到一些结论:赤道永远出现正规半日潮;月赤纬不为0时,高纬地区出现正规日潮,除赤道外其他纬度地区出现日不等现象;同时考虑月球和太阳对潮汐的效应,在朔望之时,长轴方向靠近,两潮叠加形成大潮;上、下弦之时,两潮抵消形成小潮。利用平衡潮理论计算出最大可能潮差78cm。但实际海洋潮波是在天体引潮力作用下的一种强迫波动,受海底地形起伏变化、海底摩擦以及地球自转等影响,潮波变化十分复杂,实地观测的潮高变化与平衡潮理论给出的理论潮高变化有很大差别,但潮汐变化的原理和许多规律仍可用平衡潮理论解释,比如潮汐成因、潮汐不等现象。
实际潮汐可分成许多有规律的分振动,这些分离出来的具有一定周期、一定振幅的分振动就叫分潮,实际海水的涨落总可表示为一些已知频率的振动及非潮汐因素的扰动之和。潮汐分析亦称潮汐调和分析,将任一海区的潮位变化看做是许多分潮余弦振动之和,根据最小二乘或波谱分析等数学分析方法由实测数据计算出各分潮振幅和迟角。通过潮汐调和分析,某地任意时刻的实际潮高可表示为:
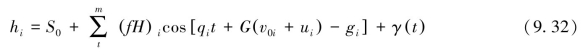
式中,S0为长期平均水位高度,i代表各分潮,fi为分潮i的交点因子,qi为分潮i的角速率,v0i为分潮i的格林尼治零时天文初相角,ui为分潮i的交点订正角,γ为扰动项,Hi为分潮i的平均振幅,gi为分潮i的格林尼治迟角,t为时间,Hi和gi分别是分潮调和常数。
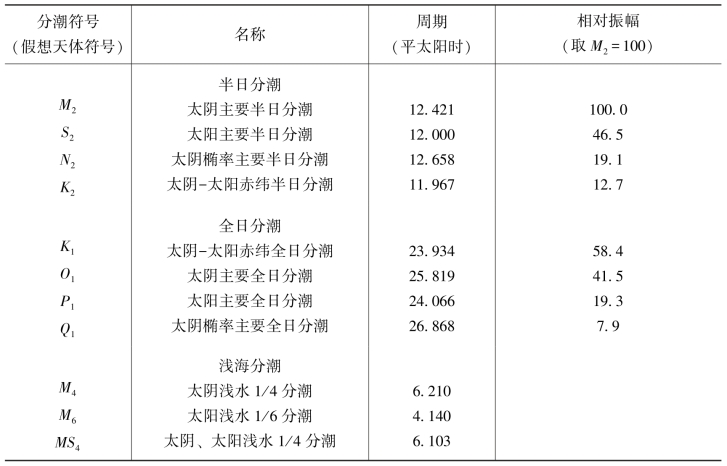
在潮汐分析过程中,hi为t时刻的观测潮高,fi、qi、G (v0i+ui )不需要潮汐观测值而预先求得(方国洪等,1986),Hi、gi为所求,将S0也看做未知数,通过较长的验潮数据,由式(9.32)即可组成误差方程,按照最小二乘原理即可求出各分潮的调和常数。在潮汐预报过程中,有了各分潮的调和常数Hi、gi,即可推算某时刻的潮高hi。表9-3列出了11个主要分潮的基本参数。
表9-3 11个主要分潮及其周期和相对振幅
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






