连续型随机变量函数的分布-《概率论与数理统计》的重要内容

连续型随机变量的函数不一定是连续型随机变量，但本书主要讨论连续型随机变量的函数是连续型随机变量的情况.对于连续型随机变量X 的函数Y，常常可利用已知Y 与X 的函数关系式Y=g（X），先求Y 的分布函数，再求Y 的概率密度函数.

例2.21　设随机变量X 的概率密度为

求随机变量Y=2X+8 的概率密度fY（y）.

解　先求Y=2X+8 的分布函数FY（y）.

于是

设X 是连续型随机变量，概率密度为fX（x），则Y=aX+b（a≠0）的概率密度为

证明留给读者.

对于连续型随机变量X，其函数Y=g（X）也是连续型随机变量时（如Y=g（x）为连续函数时），为求Y 的概率密度，可先将事件{Y≤y}转化为与之等价的事件{X∈A}，利用已知的X 的概率密度求出Y 的分布函数FY（y），再求FY（y）的导数F′Y（y）即可得Y 的概率密度fY（y）.这种通过先求分布函数，再对其求导数，从而得出概率密度的方法称为分布函数法.

例2.22　设X~fX（x）（-∞<x<+∞），求Y=X2 的概率密度.

解　先求Y 的分布函数FY（y）.

由于Y=X2≥0，故当y≤0 时，有

当y>0 时，有

于是，得到Y 的概率密度为

定理2.3　设X 为连续型随机变量，X ~fX（x）（-∞<x <+∞）.又设函数g（x）处处可导，且恒有g′（x） >0（或恒有g′（x） <0），则Y=g（X）是连续型随机变量，其概率密度为

其中α=min{g（-∞），g（+∞）}，β=max{g（-∞），g（+∞）}，h（y）是g（x）的反函数.

证　只证g′（x） >0 的情形，此时g（x）在（-∞，+∞）严格单调增加，它的反函数h（y）存在，且在（α，β）上严格单调增加，可导.下面先求Y 的分布函数FY（y）.

因为Y=g（x）在（α，β）上取值，故

当y≤α 时，FY（y）=P{Y≤y}=0.

当y≥β 时，FY（y）=P{Y≤y}=1.

当α<y<β 时，

于是，得Y 的概率密度(https://www.daowen.com)

对于g′（x） <0 的情形可以同样地证明，我们有

合并此两式，即概率密度式可得证.

特别地，若fX（x）在有限区间[a，b]以外等于零，则只需假设在[a，b]上恒有g′（x） >0（或g′（x） <0），此时α=min{g（a），g（b）}，β=max{g（a），g（b）}.

例2.23　设随机变量X~N（μ，σ2），试证明：X 的线性函数Y=aX+b（a≠0）也服从正态分布.

小知识

高斯导出误差正态分布

1809 年，约翰·卡尔·弗里德里希·高斯（Johann Carl Friedrich Gauss，1777—1855）发表了其数学和天体力学的名著《绕日天体运动的理论》.在此书末尾，他写了一节有关“数据结合”（data combination）的问题，实际涉及的就是这个误差分布的确定问题.

设真值为θ，n 个独立测量值为X1，X2，…，Xn.高斯把后者的概率取为

其中f 为待定的误差密度函数.到此为止，他的做法与拉普拉斯相同.但在往下进行时，他提出了两个创新的想法.

一是他不采取贝叶斯式的推理方式，而径直把使上式达到最大的作为θ 的估计，即使

成立的现在我们把L（θ）称为样本X1，X2，…，Xn 的似然函数，而把满足上式的称为θ 的极大似然估计.这个称呼是追随费歇尔的，因为他在1912 年发表的一篇文章中，明确提到以上概念并非针对一般参数的情形.

如果拉普拉斯采用了高斯这个想法，那他会得出，在已定误差密度为

基础上，其中m>0 为未知参数.θ 的估计是样本X1，X2，…，Xn 中位数med（X1，X2，…，Xn），即X1，X2，…，Xn 按大小排列居于正中的那一个（n 为奇数时），或居于正中的那两个的算术平均（n 为偶数时）.这个解不仅计算容易，且在实际意义上，有时比算术平均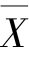 更为合理.不过，即使这样，拉普拉斯的误差分布大概也不可能取得高斯正态误差那样的地位.原因是 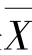是线性函数，在正态总体下有完善的小样本理论，而med（X1，X2，…，Xn），要用于推断就难于处理.另外，这里所谈的是一个特定的问题——随机测量误差是如何的分布？测量误差是由诸多因素形成，每种因素影响都不大.按中心极限定理，其分布近似于正态分布是势所必然.其实，早在1780 年左右，拉普拉斯就推广了狄莫佛的结果，得到了中心极限定理的比较一般的形式.可惜的是，他未能把这一成果用到确定误差分布的问题上来.

高斯的第二点创新的想法是，他把问题倒过来，先承认算术平均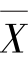 是应取的估计，然后去找误差密度函数f 以迎合这一点，即找这样的f，使由（2）式决定的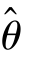就是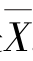.高斯证明了只有在

条件下才能成立，这里σ>0 为常数，这就是正态分布N（0，σ2）.

高斯这项工作对后世的影响极大，他使正态分布同时有了“高斯分布”的名称，后世之所以多将最小二乘法的发明权归之于他，也是出于这一工作.高斯是一个伟大的数学家，重要的贡献不胜枚举.但现今德国10 马克的印有高斯头像的钞票，其上还印有正态分布N（μ，σ2）的密度曲线.这传达了一种想法：在高斯的一切科学贡献中，其对人类文明影响最大者，就是这一项.

在高斯刚做出这个发现之初，也许人们还只能从其理论的简化上来评价其优越性，其全部影响还不能充分看出来.这要到20 世纪正态小样本理论充分发展起来以后.

拉普拉斯很快得知高斯的工作，并马上将其与他发现的中心极限定理联系起来，为此，他在即将发表的一篇文章（发表于1810 年）上加上了一点补充，指出如若误差可看成许多量的叠加，根据他的中心极限定理，误差理应有高斯分布.这是历史上第一次提到所谓“元误差学说”——误差是由大量的、由种种原因产生的元误差叠加而成.后来到1837 年，海根在一篇论文中正式提出了这个学说.其实，他提出的形式有相当大的局限性：海根把误差设想成个数很多的、独立同分布的“元误差”ξ1，ξ2，…，ξn 之和，每个ξi 只取±a 两值，其概率都是，由此出发，按狄莫佛的中心极限定理，立即就得出误差（近似地）服从正态分布.

拉普拉斯所指出的这一点有重大的意义，在于他给误差的正态理论一个更自然合理、更令人信服的解释.因为，高斯的说法有一点循环论证的气味：由于算术平均是优良的，推出误差必须服从正态分布；反过来，由后一结论又推出算术平均及最小二乘估计的优良性，故必须认定这二者之一（算术平均的优良性，误差的正态性）为出发点.但算术平均到底并没有自行成立的理由，以它作为理论中一个预设的出发点，终觉有其不足之处.拉普拉斯的理论把这断裂的一环连接起来，使之成为一个和谐的整体，实有着极重大的意义.