(1)一个正态总体情形
设简单随机样本X1,X2,…,Xn来自正态总体X~N(μ,σ2).记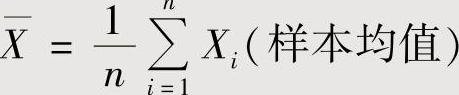 ,
,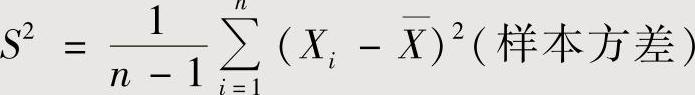 ,则
,则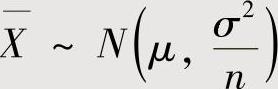 ,即
,即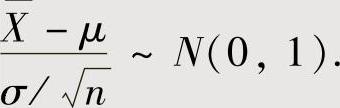
(2)两个正态总体情形
设简单随机样本X1,X2,…,Xn1与Y1,Y2,…,Yn2分别来自相互独立正态总体X~N(μ1,σ21)和Y~N(μ2,σ22),记
则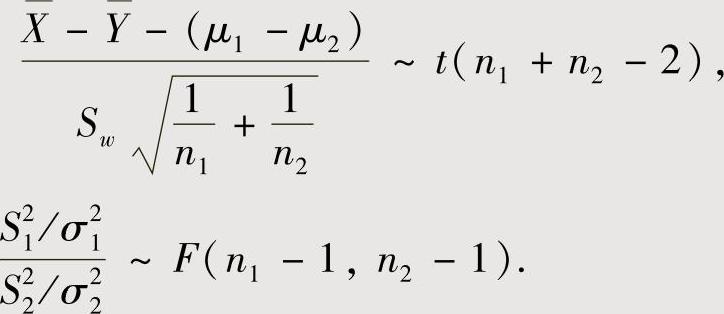
例15.1 设X1,X2,X3,X4是来自总体X~N(0,22)的简单随机样本,并且统计量U=a(X1-2X2)2+b(3X3-4X4)2~χ2(n)(a>0,b>0),求常数a,b及自由度n之值.
精解 由于U只有两个平方项,所以n=2,下面计算a,b之值.按χ2分布的定义,要使U~χ2(2),必须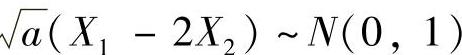 ,
,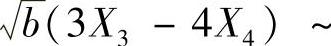
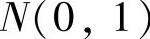 .于是,
.于是,
由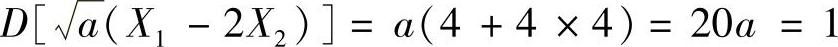 得
得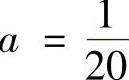 ,由
,由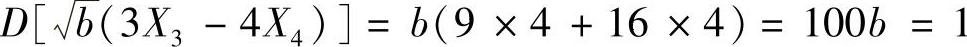 得
得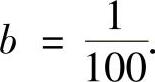
例15.2 设X1,X2,…,X9是来自总体N(μ,σ2)的简单随机样本,记
求统计量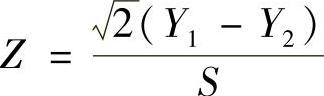 所服从的分布.
所服从的分布.
精解 由于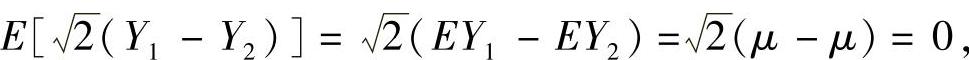
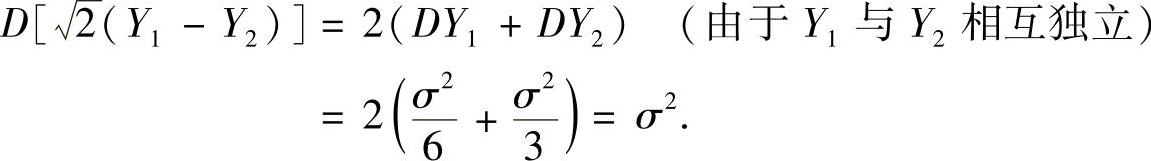
所以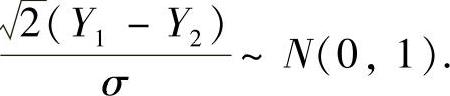
由于S2是样本X7,X8,X9的方差,所以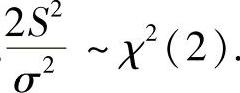 此外,
此外,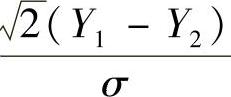 与
与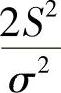 相互独立(这是由于Y1,Y2都与S2相互独立).
相互独立(这是由于Y1,Y2都与S2相互独立).
因此,由t分布定义得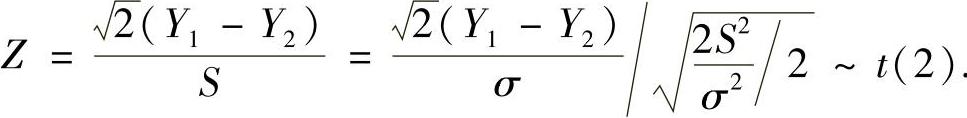
例15.3 设X1,X2,…,X15是来自总体(0,22)的简单随机样本,求统计量
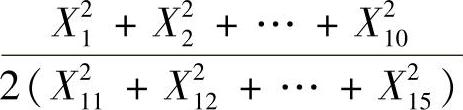 所服从的分布.(https://www.daowen.com)
所服从的分布.(https://www.daowen.com)
精解 由于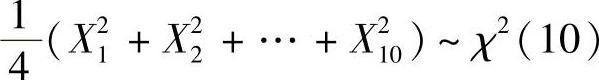 ,
, ,所以由F分布定义得
,所以由F分布定义得
例15.4 设X1,X2,…,Xn(n>2)是来自总体X~N(0,1)的简单随机样本,记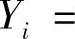
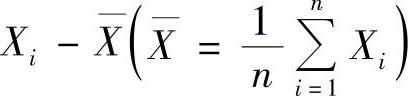 ,i=1,2,…,n.求:
,i=1,2,…,n.求:
(1)求统计量Y1所服从的分布;
(2)统计量Y1与Yn的协方差Cov(Y1,Yn).
精解 (1)由于X1,X2,…,Xn相互独立,且都服从N(0,1),所以
服从正态分布.
由于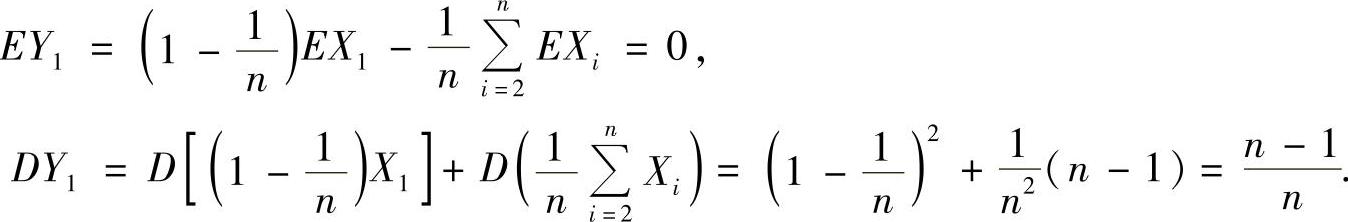
因此,Y1~N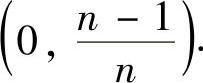
例15.5 设X1,X2,…,Xn是总体N(0,1)的简单随机样本,记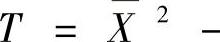
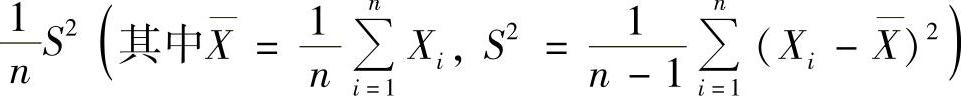 ,求统计量T的方差.
,求统计量T的方差.
精解 由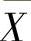 与S2相互独立知
与S2相互独立知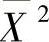 与
与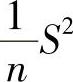 相互独立,所以
相互独立,所以
其中,由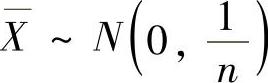 知
知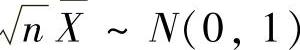 ,从而有
,从而有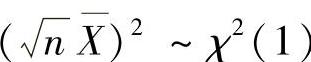 ,因此
,因此
由(n-1)S2~χ2(n-1)知
将式(2)、式(3)代入式(1)得
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





