平均交互信息量不增：信息论基础与工程应用

在实际通信系统中,常需对信道传输的数据作适当处理,若把数据处理装置亦看作是一个信道,这就由两个信道串接,组成了一个串接信道。

设信道I和信道II串接,组成图3.16所示串接信道。信道I的输入符号集X:{a1,a2,…,ar}输出符号集Y:{b1,b2,…,bs},输出符号集Z:{c1,c2,…,cL}。又设,信道I的传递概率P(Y/X):{p(bj/ai)(i=1,2,…,s)},信道II的传递概率P(Z/XY):{p(ck/aibj)(i=1,2,…,r;j=1,2,…,s;k=1,2,…,L)}。且假定p(aibjck)＞0(i=1,2,…,r;j=1,2,…s,k=1,2,…,L)

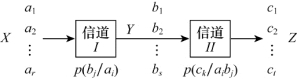
图3.16　串接信道

由一个信道组成的通信系统只有输入、输出两个随机变量X和Y。由两个信道串接组成的串接信道中,就有X、Y、Z三个随机变量,那么,由三个随机变量构成的随机变量序列(XYZ),在信息传输上又有什么新的特点和规律呢?

定理3.5　设由两个信道串接构成随机变量序列(XYZ),则

当且仅当

即(XYZ)是Markov链时,才有

【证明】根据平均交互信息量的定义,有

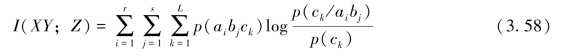
而

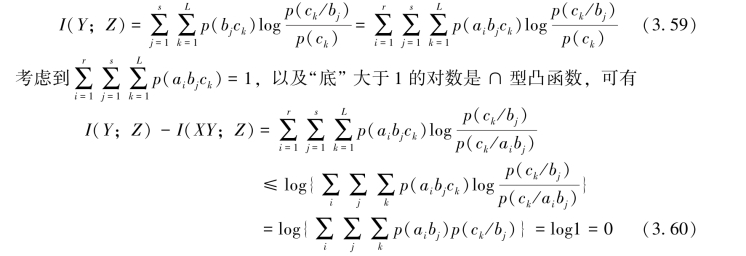
即证得

由式(3.56)有

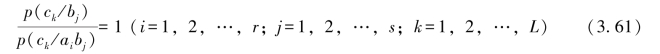
则由式(3.60)有

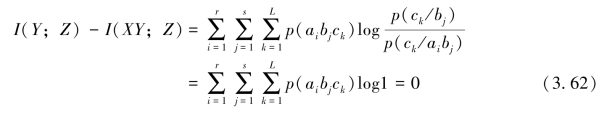
即证得

定理3.6　设由两个信道串接构成随机变量序列(XYZ),则

当且仅当

即(YXZ)是Markov链时,才有

【证明】　根据平均交互信息量的定义,有

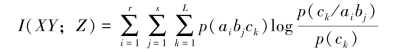
而

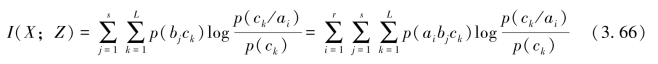
即证得

由式(3.64)有

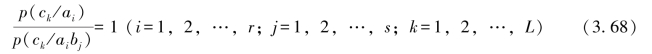
则由式(3.67)有

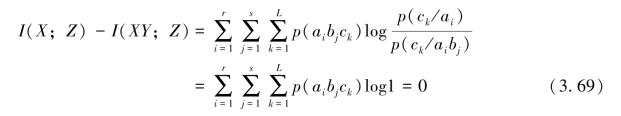
即证得

定理3.7　设由两个信道串接构成的随机变量序列(XYZ)。当

即当(XYZ)是Markov链时,有

当且仅当

即(YXZ)亦是Markov链时,有

【证明】由定理3.5可知当随机变量序列(XYZ)是Markov链时,有

由定理3.6可知,在随机变量序列(YXZ)不是Markov链的情况下,有

由式(3.74)和式(3.75)可得,当(XYZ)是Markov链,而(YXZ)不是Markov链的情况下,有

由定理3.6可知,当(YXZ)是Markov链时,有

则由式(3.74)、式(3.75)证得,当(XYZ)和(YXZ)都是Markov链时,即

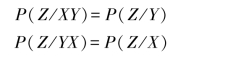
时,有

证毕。

对于图3.16所示串接信道,在工程上一般把随机变量序列(XYZ)看作Markov链,整个串接信道的传递概率频p(ck/ai)(i=1,2,…,r;k=1,2,…,L)求得,即有

这就是说,整个串接信道的信道矩阵[P](rxL阶),等于信道I的信道矩阵[PI](rxs阶)与信道II的信道矩阵[PII](sxL)阶的连乘,即

若要求随机变量序列(XYZ)和(YXZ)都是Markov链,则要有

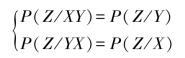
即

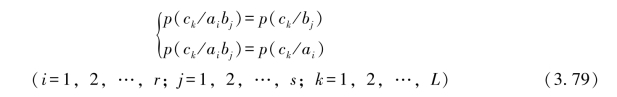
即必须有

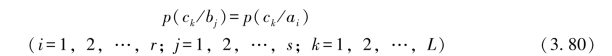
这就是说,整个串接信道的信道矩阵[P]与信道II的信道矩阵[PII]要完全一样,即要有

显然,信道I的矩阵[PI]是(sxs)阶单位矩阵,是式(3.81)能得到满足的一种情况,这时有

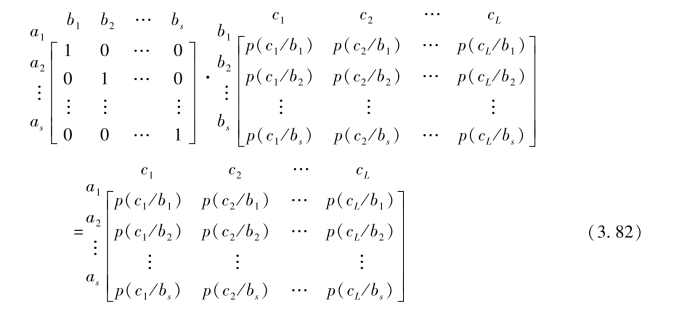
式(3.82)指明,当信道I是一一对应的确定关系的一般无噪信道时,随机变量序列(XYZ)与随机变量序列(XYZ)一样,亦是Markov链。

由以上分析可以得到这样一个结论:在一般情况下(XYZ)是Markov链,输出随机变量Z通过信道II一个信道,获取关于随机变量Y的信息量I(Y;Z),总是比输出随机变量Z通过信道II、信道I两个信道,获取关于随机变量X的信息量I(X;Z)大,这就是说,随机变量Y通过信道I到随机变量X,总是要丢失一部分信息量(如图3.17)。只有当随机变量序列(YXZ)亦是Markov链(如信道I是一一对应确定关系的一般无噪信道)时,随机变量Y到随机变量X才不会丢失信息量,因而从Z中获取关于Y的信息量I(Y;Z),才与从Z中获取关于X的信息量I(X;Z)相等。

定理3.8　设由两个信道串接构成随机变量序列(XYZ),当

即当(XYZ)是Markov链时,有

当且仅当

即(YZX)亦是Markov链时,才有

【证明】由概率一般运算规则有

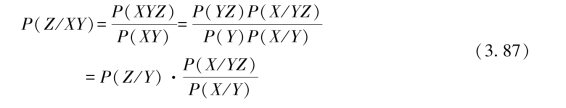
由式(3.83),有

这表明,当随机变量序列(XYZ)是Markov链时,随机变量序列(ZYX)亦是Markov链,根据定理3.5,有

在一般情况下,随机变量序列(YZX)不是Markov链,根据定理3.6,有

由式(3.89)和式(3.90),有

根据平均交互信息量的交互性,可证得

当随机变量序列(YZX)亦是Markov链时,根据定理3.6,有

由式(3.89)有

(https://www.daowen.com)

根据平均交互信息量的交互性,证得

这样定理就得到了证明。

对于图3.16所示串接信道,在一般情况下,随机变量序列(XYZ)都可看作是Markov链,即随机变量序列(ZYX)亦可看作Markov链。如要求随机变量序列(YZX)同时也是Markov链,则必须有

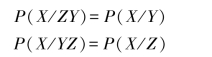
即有

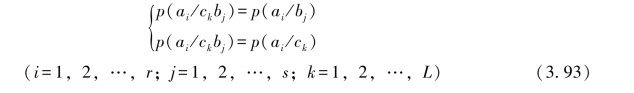
即必须有

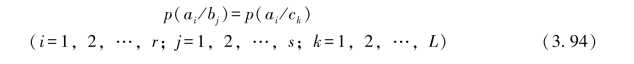
而

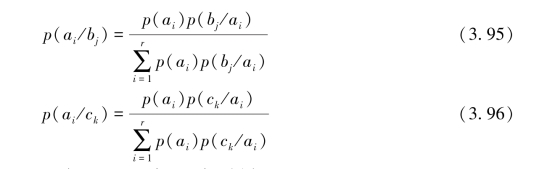
由式(3.94)以及式(3.95)、式(3.96)可知,则必须有

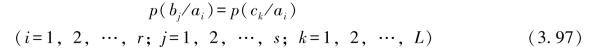
这说明,如果要求随机变量序列(ZYX)是Markov链的条件下,随机变量序列(YZX)亦是Markov链,则必须要求图3.16串接信道的信道矩阵[P]与信道I的信道矩阵[PI]完全相同,即必须有

显然,信道II的信道矩阵[PII]是(s×s)阶单位矩阵,是式(3.98)能得到满足的一种情况,这时有

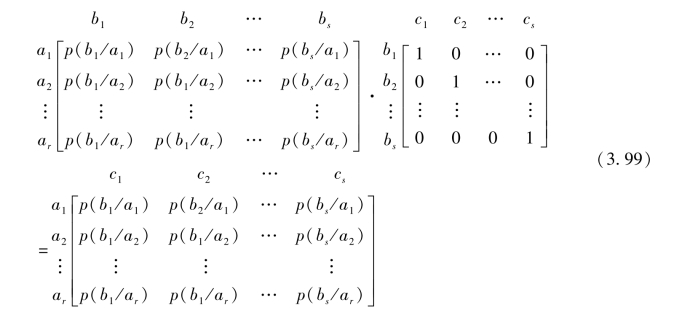
这表明,当信道II是一一对应的确定关系的一般无噪信道时,随机变量序列(YZX)与随机变量序列(ZYX)一样,亦是Markov链。

由以上分析可得到这样一个结论:对于图3.16串接信道,在一般情况下,由于随机变量序列(XYZ)可看作是Markov链,所以随机变量序列(ZYX)亦可看作是Markov链。随机变量X通过信道I获取关于随机变量Y的信息量I(X;Y),总比随机变量X通过信道I和信道II两个信道,获取关于随机变量Z的信息量I(X;Z)大。这就是说,随机变量Y通过信道II到随机变量Z,总要丢失一部分信息量(如图3.18)。只有当随机变量序列(YZX)亦是Markov链(如信道II是一一对应确定关系的一般无噪信道时),随机变量Y到随机变量Z才不会丢失信息量。因而从随机变量X中获取关于随机变量Y的信息量I(X;Y),才与从随机变量X中获取关于随机变量Z的信息量I(X;Z)相等。

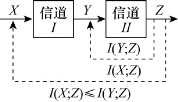
图3.17　关注信道II

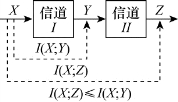
图3.18　关注信道I

【例3.9】设信道I和信道II相接,组成图3.19串接信道。若随机变量序列(XYZ)是Markov链,试证明I(X;Z)=I(X;Y)。

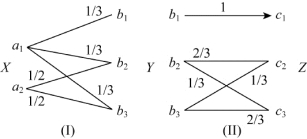
图3.19　(XYZ)构成Markov链

解:因为随机变量序列(XYZ)是Markov链,由图3.19可知,串接信道的信道矩阵

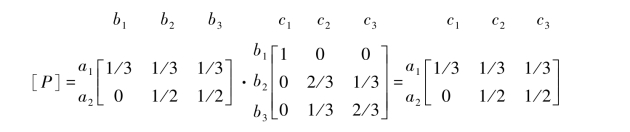
由于串接信道的信道矩阵[P]与信道I的信道矩阵[PI]完全一致,所以有

根据式(3.97)、(3.96)、(3.95)、(3.94)、(3.93),随机变量序列(YZX)亦是Markov链。根据定理3.8,可证得

这一特例说明,在(XYZ)是Markov链的条件下,信道II是一一对应确定关系的一般无噪信道,是式(3.84)中等式(3.85)成立的必要条件,但不是充分条件。

推论　设有两个信道串接构成随机变量序列(XYZ)。若随机变量序列(XYZ)是Markov链,则有

【证明】因为随机变量序列(XYZ)是Markov链,则由定理3.7有

又因为当(XYZ)是Markov链时,随机变量序列(ZYX)亦是Markov链,由定理3.8,有I(X;Z)≤I(X;Y)

即证得,当随机变量序量(XYZ)是Markov链时,有

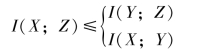
这样,推论就得到了证明。平均交互信息量I(X;Z)与I(Y;Z)和I(X;Y)之间的关系综合表示为图3.20所示。

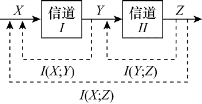
图3.20　数据处理

推论指出,若以Z作为观察点,把信道I看作是一个数据处理装置(如图3.21),随机变量序列(XYZ)是Markov链。因随机变量Y经过处理后,变成随机变量X,则从随机变量Z中获取关于随机变量X的平均交互信息量I(X;Z),不会超过数据处理前从随机变量Z中获取关于随机变量Y的平均交互信息量I(Y;Z),最多两者相等。这就是说,把随机变量Y变成随机变量X的数据处理过程,总是要丢失一部分信息。只有当随机变量序列(YXZ)亦是Markov链时(数据处理是一一对应确定关系时),数据处理过程才不会丢失信息。

推论又指出,若以X作为观察点,把信道II看作是一个数据处理装置,如图3.22所示,随机变量序列(ZYX)是Markov链。因随机变量Y经过数据处理后,变成随机变量Z,从随机变量X中获取关于随机变量Z的平均交互信息量I(X;Z),不会超过数据处理前从随机变量X中获取关于随机变量Y的平均交互信息量I(X;Y),最多两者相等。这就是说,把随机变量Y变成随机变量Z的数据处理过程,总是要丢失一部分信息。只有当随机变量序列(YZX)亦是Markov链时(数据处理是一一对应的确定关系时),数据处理过程才不会丢失信息。

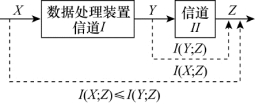
图3.21　串接信道

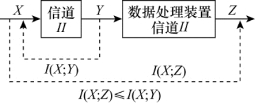
图3.22　串接信道

综合推论所指出的两方面的结论,可以得到一个总的结论:任何无源数据处理过程都要丢失一部分信息量,最多不丢失信息量,但一定不会增加信息量。由定理3.5、3.6、3.7、3.8及其推论所阐明的平均交互信息量的不增性,一般通称为数据处理定理。

数据处理定理是信息传输的重要规律。把数据处理定理与前面讨论的平均交互信息量的极值性结合起来,就可导出信息传输和处理的一个完整的概念,如图3.23(a)和(b)所示。对于信源X来说,经信息传输或信息处理,最终从随机变量Q中获取关于信源X的平均交互信息量I(X;Q),绝对不会超过信源X本身含有的平均信息量H(X),最多等于信源X本身含有的平均信息量H(X)。信息所经过的传输信道或数据处理装置越多,丢失的信息量就可能越多。即有

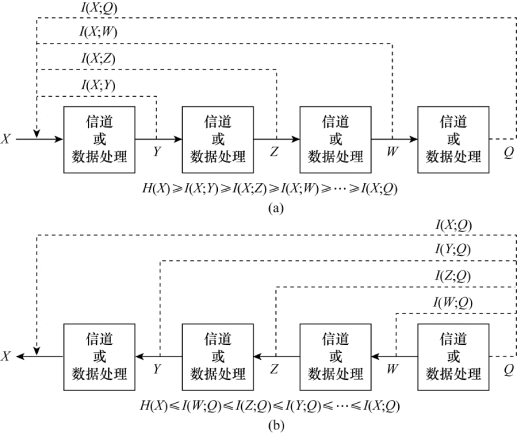
图3.23(b)

对于随机变量Q来说,经信息传输或信息处理,最终从随机变量X中获取关于随机变量Q的平均交互信息量I(Q;X),绝不会超过随机变量Q本身含有的平均信息量H(Q),最多等于H(Q)。信息所经过的传输信道或数据处理装置越多,丢失的信息量就可能越多。即有

在传输或处理过程中,一旦在某一环节(信道或处理装置)丢失一部分信息,以后的系统不管怎样传输或处理,如不能接触到丢失信息环节的输入端(如多次测量),就不能再恢复已丢失的信息。

【例3.10】设有三个二进制对称信道(BSC),串接组成图3.24所示串接信道。随机变量序列(XYZW)是Markov链。若信源X:{0,1}是等概信源,试求平均交互信息量I(X;Y)、I(X;Z)、I(X;W),并比较它们的大小。

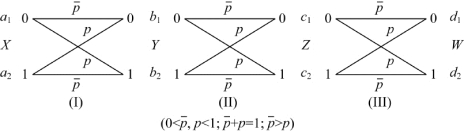
图3.24　三个信道串联

解:(1)因为信道I的矩阵为

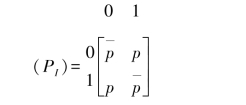
信源X的概率分布为

所以,随机变量Y的概率分布为

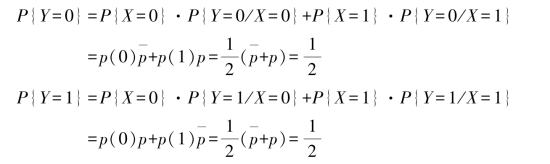
则随机变量Y的熵

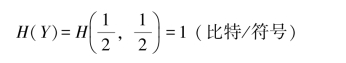
由信道I的信道矩阵[PI],有

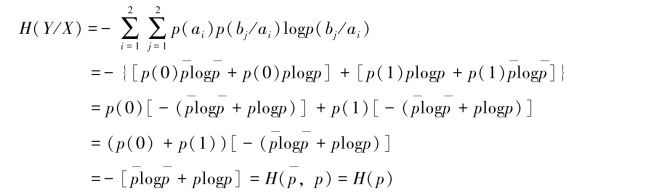
所以,信道I的平均交互信息量

(2)因为随机变量序列(XYZW)是Markov链,所以信道I、信道II的串接信道(XZ)的信道矩阵,等于信道I矩阵[PI]与信道II矩阵[PII]的连乘,即有

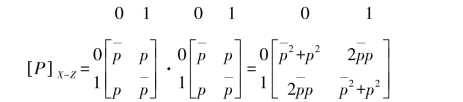
随机变量Z的概率分布为

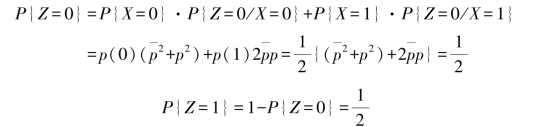
则得随机变量Z的熵

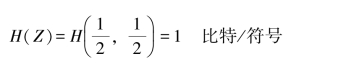
由串接信道(X-Z)的信道矩阵[P]X-Z,有

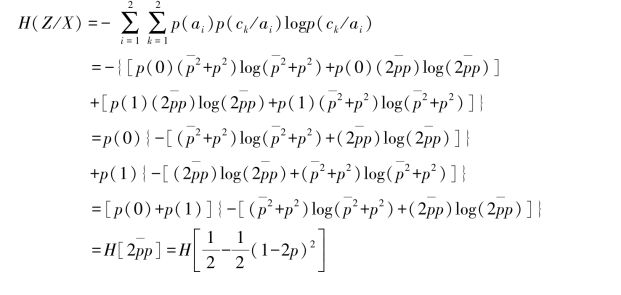
则

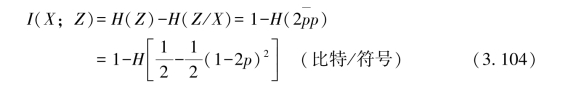
同理可得

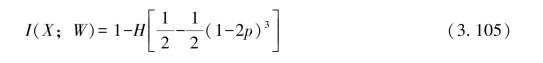
则可有

(3)一般地,设有N(大于1的正整数)个二进制对称信道(BSC),串接成如图3.25所示的串接信道。当信源X是等概分布时,同理可证:

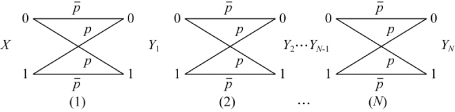
图3.25　串接信道

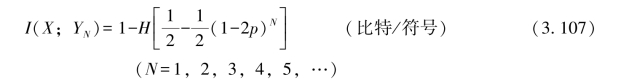
则有

(3.108)式是由N个二进制对称信道(BSC)组成的串接信道,当信源X:{0,1}为等概信源时,数据处理定理的具体表现。

实践:信道容量的迭代算法

【已知】信源符号个数r、信宿符号个数s、信道转移概率矩阵P=(pji)r×s。

【算法】

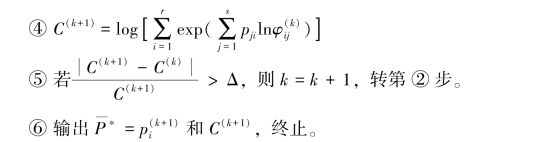
【要求】

(1)输入:任意的一个信道转移概率矩阵。信源符号个数、信宿符号个数和每个具体的转移概率在运行时从键盘输入。

(2)输出:最佳信源分布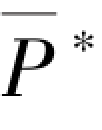,信道容量C。