Diffie-Hellman密钥交换算法的实现

Diffie 和Hellman 在其里程碑意义的文章中， 虽然给出了密码的思想， 但是既没有给出真正意义上的公钥密码实例， 也没能找出一个真正带陷门的单向函数。 然而， 他们给出了单向函数的实例， 并且基于此提出了Diffie-Hellman 密钥交换算法。

Diffie-Hellman 密钥交换算法是第一个公钥方案， 使用在一些商业产品中。 该方案不能用于交换任意信息， 允许两个用户安全地建立一个秘密信息用于后续的通信过程， 该秘密信息仅为两个参与者知道。 Diffie-Hellman 密钥交换算法的安全性依赖于有限域上计算离散对数的难度。

1. Diffie-Hellman 密钥交换算法的数学基础

素数p 的原根定义: 如果a 是素数p 的原根， 则数a mod p，a2 mod p，…，ap -1mod p 是不同的且包含1 ～p-1 的整数的某种排列， 即{a mod p，a2 mod p，…，ap -1mod p} ={1，2，…，

对任意的整数b 和素数p 的原根a， 可以找到唯一的指数x 满足

将x 称为b 以a mod p 为底数的指数(离散对数)， 记作x=logab mod p。

2. Diffie-Hellman 密钥交换算法描述

(1) 双方选择素数p 以及p 的一个原根a。

(2) 用户A 选择一个随机数xA(xA ＜p)， 计算YA =axA mod p。

(3) 用户B 选择一个随机数xB(xB ＜p)， 计算YB =axB mod p。

(4) 一方保密X 值， 而将Y 值交换给对方。

(5) 用户A 计算出KA =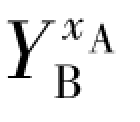mod p。

(6) 用户B 计算出KB =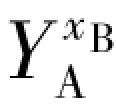 mod p。

(7) 双方获得一个共享密钥(axAxBmod p)。(https://www.daowen.com)

说明: 素数p 以及p 的原根a 可由一方选择后发给对方。

3. Diffie-Hellman 实例

(1) 用户Alice 和Bob 想交换密钥: 约定素数p=353， a=3。

(2) 随机选择密钥: A 选择xA =97， B 选择xB =233。

(3) 计算公钥。

(4) 计算共享的会话密钥。

4. Diffie-Hellman 密钥交换的安全性分析

已知axmod p 和aymod p， 计算axy mod p 的问题称为Diffie-Hellman 问题。 人们认为这个问题也是很难处理的。

在上述密钥分配过程中， 攻击者很容易获得ax mod p、 ay mod p。 由于计算离散对数的困难性， 所以很难计算出x 和y。

Diffie-Hellman 密钥分配方案必须结合实体认证才有用， 否则会受到中间入侵攻击。

中间人O 攻击的过程如下:

(1) 用户A、 B 双方选择素数p 以及p 的一个原根a (假定中间人O 知道)。

说明: O 无法计算出axAxB mod p； O 永远必须实时截获并冒充转发， 否则会被发现。