Hagen-Poiseuille流：微通道间流体的流动

假设流体在压力梯度的作用下在圆管道内产生轴向单向流，如图1.7所示，其中半径为 R. 这里流体是粘性不可压牛顿流体. 在柱面坐标系中的控制方程如下:

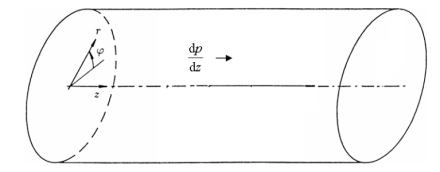
图1.7　圆管道内的流动

连续性方程:

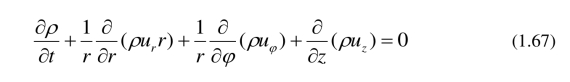
动量守恒方程 (Navier-Stokes equations):

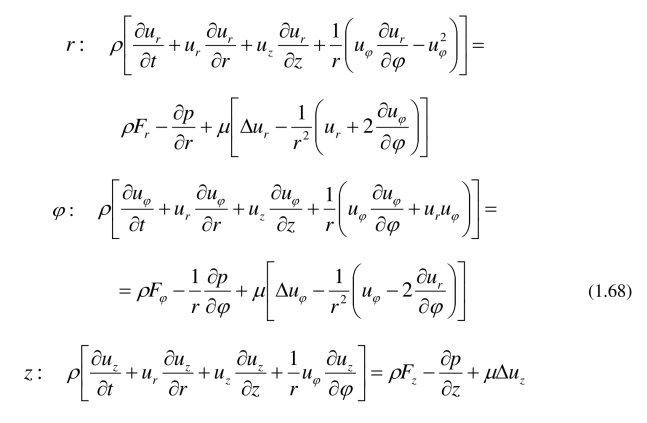
这里,

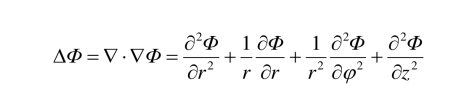
由于速度分量 ur 和 φu 都等于零，并且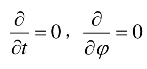，因此控制方程变为(没考虑力 F )以下形式.

连续性方程:

动量守恒方程 (Navier-Stokes equations):

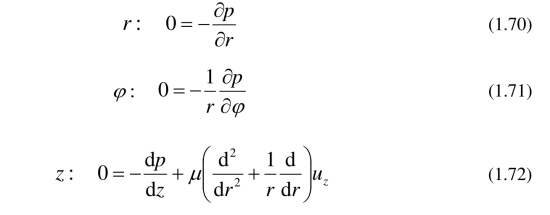
方程 (1.69) 说明了速度与变量z无关，uz 仅依赖于变量r. 另外，方程 (1.70) 和 (1.71) 说明了压力仅依赖于变量 z. 因此，方程 (1.72) 也可以表示如下:

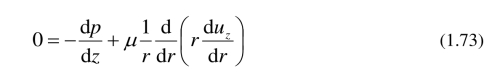
把方程 (1.73) 积分两次，得

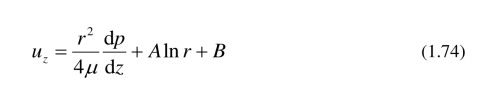
速度在管道中心有界，在边界上满足无滑移边界条件

由边界条件 (1.75) 可得

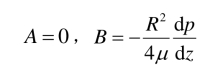
因此

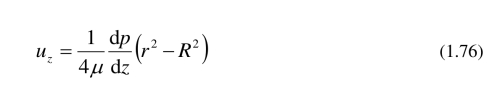
在管道中心r = 0处，速度达到最大值:

(https://www.daowen.com)

流率为

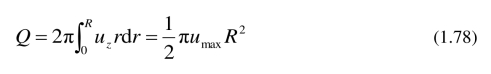
平均速度为

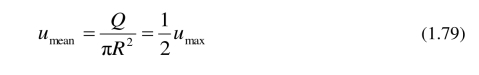
也就是

我们注意到

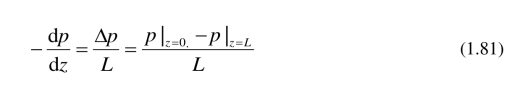
这里L是管道长度.

切应力是

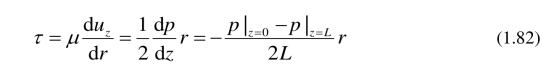
切应力在管道壁面上最大,

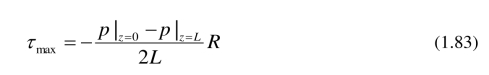
利用 (1.80) 和 (1.81) 可得

管道阻力系数的定义为

将 (1.84) 代入上式得

其中

是对平均速度而言的雷诺数. 从 (1.86) 可知阻力系数与雷诺数成反比.

由 (1.77) 和 (1.78) 可得

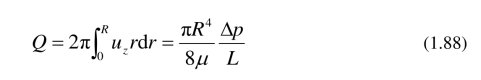
该结果与实验结果非常吻合，可以用该公式计算粘性系数.