伴随矩阵的定义 设A为n阶方阵，行列式
的各元素的代数余子式所构成的如下方阵，称为方阵A的伴随矩阵，记作A.即
例2 求方阵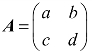
的伴随矩阵.
解：A11=d，A12=−c，A21=−b，A22=a，从而
伴随矩阵的性质 
，且
.
证明：设A=(aij)n×n，可得
，于是
其中，
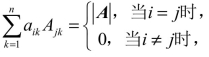于是
同理 
.
上式两边同时取行列式有，
，于是
.
定理1 方阵A可逆的充要条件为
，且
.
证明：(⇒)A可逆，则存在A−1使AA−1=A−1A=E，于是
，所以
.
(⇐)由
且
可得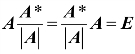
，于是A 可逆，且
.
当
时，方阵A称为非奇异方阵；当
时，方阵A称为奇异方阵.
例3 求方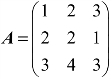阵
的逆矩阵.
解：由于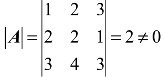
，所以A可逆，而
，
，
，
，
，
，
，
，
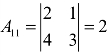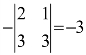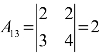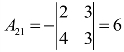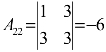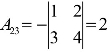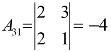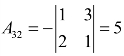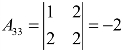，于是
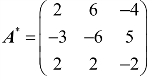，则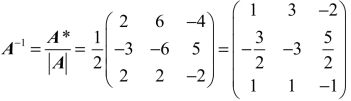
.
例4 已知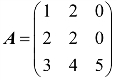
，A是A的伴随矩阵，求(A∗)−1.
解：
，A可逆，从而
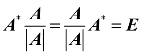，于是，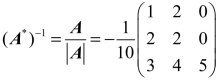
.
定理2 设A为n阶方阵，则方阵A可逆的另一充要条件为存在n阶方阵B使得式子AB=E（或BA=E）成立.
证明：(⇒)A可逆，则由定义可得，存在n阶方阵B使AB=E.
(⇐)若AB=E，则
，故
，于是A可逆.
例5 已知n阶方阵A满足A2−A−2E=O，其中A给定，E为n阶单位矩阵，证明：A、A+2E均可逆，并求它们的逆矩阵.
证明：由A2−A−2E=O，得
A( A−E)=2E，
⇒
.
由定理2可得A可逆，且
.
又由A2−A−2E=O，
⇒(A+2E)(A−3E)+4E=O
⇒
故A+2E可逆，且
.
方阵的逆矩阵满足下面运算律：
（1）若A可逆，则A−1也可逆，且(A−1)−1=A；
（2）若A可逆，数k≠0，则kA可逆，且
；
（3）若A,B为同阶方阵且均可逆，则AB也可逆，且(AB)−1=B−1A−1；
（4）若A可逆，则AT也可逆，且(AT)−1=(A−1)T；
（5）若A可逆，则有
.(https://www.daowen.com)
例6 解方程组AXB=C，其中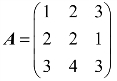
，
，
.
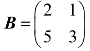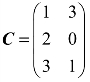解：若A−1，B−1都存在，则A−1AXBB−1=A−1CB−1，即X=A−1CB−1.
由例3可知A可逆，而
，所以B也可逆，且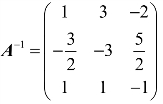
，
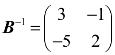，于是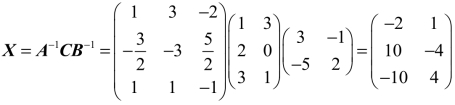
.
在逆矩阵存在的前提下，利用逆矩阵求解矩阵方程，有下面的结果：
（1）若AX=B，则X=A−1B；
（2）若XA=B，则X=BA−1；
（3）若AXB=C，则X=A−1CB−1.
练习题（三）
1.判断下列矩阵是否可逆.
（1）
；
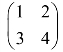（2）
；
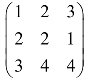（3）
.
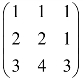2.求下列矩阵的伴随矩阵.
（1）
；
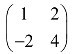（2）
；
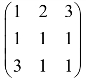（3）
.
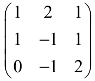3.利用伴随矩阵求下列矩阵的逆矩阵.
（1）
；
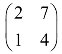（2）
；
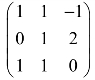（3）
.
4.解以下矩阵方程.
（1）
；
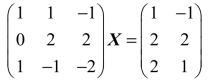（2）
.
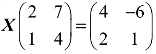5.选择题.
（1）设A,B,C均为n阶方阵，且ABC=E，则下列矩阵为单位矩阵的是（ ）.
A.ACB B.CBA C.BAC D.BCA
（2）设A为n阶非零矩阵，E为n阶单位矩阵，若A3=O，则（ ）.
A.E−A不可逆，E+A不可逆 B.E−A不可逆，E+A可逆
C.E−A可逆，E+A可逆 D.E−A可逆，E+A不可逆
6.证明题.
（1）已知n阶方阵A满足A2−2A+E=O，其中A给定，E为n阶单位矩阵，证明：A,A+2E均可逆，并求它们的逆矩阵；
（2）设A,B均为n阶方阵，且B和E−AB都是可逆阵，证明：E−BA可逆.
7.设A为3阶方阵，已知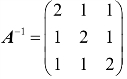
，求
.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
