趣味数学：π的精确度追求，707位小数点记录

在古代阿拉伯数学家穆罕默德·本·木兹所著的《代数学》中有段话代表了人们对圆周计算方法的描述：

最好的方法是把圆的直径乘以，这是最便捷的方法，只有真主才能有比这更快的方法。

现在我们都知道，阿基米德推算出的这个并不是完全精确的，而且经历了历史的长河，我们也知道了圆周和直径的比值是不可能用任何一个简单而精准的数值表达出来的，这个数值永远都只能是个近似值。

虽然在日常生活中，这个近似值已经足够了，但是数学家们对于这个数值的精确度却有孜孜不倦的追求。

16世纪时，有位荷兰数学家鲁多尔夫将π的数值精确到了小数点后35位，并将这个数值刻在了自己的墓碑上：

3.141，592，653，589，793，238，462，643，383，279，502，88……

19世纪时，德国数学家圣克斯又计算出了π的小数点后707位！其实无论是理论上，还是实际运用中，这样精确的π都是没有什么意义的。但是数学家们为了乐趣，甚至是为了追求“破纪录”的快乐，仍然孜孜不倦地追求π的精确度。(https://www.daowen.com)

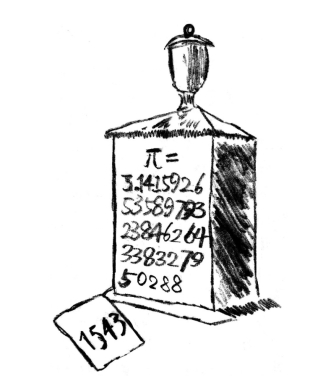
图43　数学家引以为豪的墓碑

在2025年到2025年之间，来自曼切斯特大学的菲尔古松和来自华盛顿的伦其将π后面小数点的位数扩展到了808位，并且发现了之前圣克斯计算的数据中，从528位开始都是错误的，这令他们感到欣喜不已。

数学家格拉维曾经举过一个例子，根据这个例子我们可以清楚看出，将π计算到100之后是没有任何意义的。如果说我们知道地球的精确直径，想要精确地计算出地球赤道的圆周长，精确到1厘米，我们也只需要小数点后9位数字的π就足够了。假设我们使用了小数点后18位的π值，计算出来的差距也不超过0.0001毫米，甚至远远比不上一根头发丝那么粗。

对于日常生活中的一般计算，小数点后两位数（3.14）就足够了；对于更加精确的计算，也只需要小数点后四位数（3.1416）即可，最后的6是根据5四舍五入的结果。