影子价格对应变动原材料供应和购买决策

若线性规划（LP）的最优单纯形表为T（B），最优基为B，现在我们来讨论，如果参数bs的改变量Δbs（其他bi均不变）没有超出式（2－24）规定的范围，那么，当Δbs＝1时，Δf＊＝？

由对偶理论知道，最优基B对应的单纯形因子

为对偶问题（LD）的最优解，且（LP）的最优值

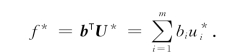
因为当bs变化而基B仍保持最优基地位时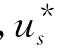，并不改变，所以若把f＊视为b1，…，bm的函数，则当Δbs＝1时，有

下面我们对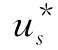的经济意义作进一步的解释.

假设有一家工厂利用m种资源生产n种产品.已知每单位j＃产品的利润为cj，i＃资源供应上限为bi，生产一个单位j＃产品所耗费的i＃资源的定额为aij.那么，每种产品各生产多少，使工厂获利最大？

设j＃产品的生产数量为xj.则该问题的线性规划模型为

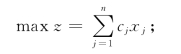
（1）验证X＝（x1，x2，x3）T＝（5，0，3）T为该问题的最优解；

（2）若是原材料的供应由30变为40，而这10个单位的原材料的购买价格为6，问要不要购买这10个单位的原材料？利润能否增加？

（3）若是外单位准备从工厂购买产品的原材料，从现有的30单位原材料中购买4个单位，每单位原材料价格议定为3，工厂是否会考虑买给外单位？利润是上升还是减少？变化多少？

（2）必须先对原材料b2进行灵敏度分析，要求：

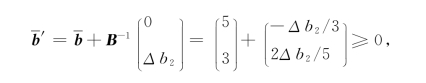
从而，当原材料的改变量Δb2∈［－7.5，15］，现在的生产品种仍然不变：

若是原材料由30变为40，可见Δb2＝10∈［－7.5，15］，可以考虑购买这10个单位的原材料.一个单位的原材料的影子价格为r5＝1，利润能够上升Δf＝10×1－6＝4.

（3）如果原材料供应减少1个单位，目标函数z仅仅减少影子价格r5＝1，现在卖给外单位可以收益2单位，并且Δb2＝－4∈［－7.5，15］，所以工厂可以考虑卖给外单位，利润上升，上升4×（2－1）＝4.

所以说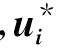，是在实现最优值时对于第i种资源的一种价格估计，这种估计是针对具体企业具体产品而存在的一种特殊价格.影子价格与市场价格既有联系又有区别，是市场价格从不同角度来看的“影子”，可以当作企业的一种经营管理方法，用于内部核算、分析和决策.

下面，我们再来讨论生产活动中的另一类问题.

设有一个工业系统，它拥有n种不同类型的生产工厂，生产m种社会所需的产品，已知一年内社会对i＃产品的最低需求量为bi，又知一年内j＃生产工厂的运行成本为cj、生产i＃产品的数量为aij.那么，在保证满足社会对m种产品需求量的前提下，每种类型生产工厂各应投入多少家运行，才能使总成本达到最小？

设xj为投入运行的j＃生产工厂的厂家数量，则我们得到如下线性规划模型：

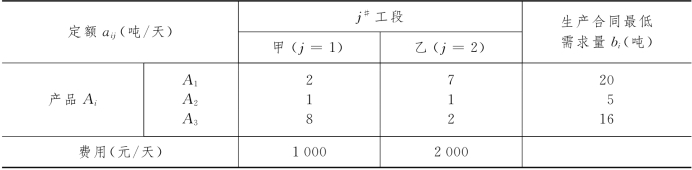
例2－20　某工厂有甲、乙两个车间工段可生产A1，A2和A33类产品，各工段开工一天生产3类产品的数量、费用以及合同对3类产品的最低需求量由表2－19给出.问各工段开工几天，能使生产合同的要求得到满足，并能使费用最低？试对b1作灵敏度分析，并求每吨A1类产品的合理成本.

表2－19(https://www.daowen.com)

解　设x1，x2分别为工段甲、乙开工的天数，则得模型

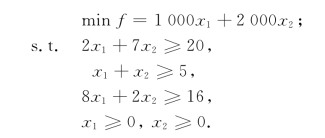
对上述模型引进剩余变量x3，x4，x5并用对偶单纯形法求解，得如表2－20所示的最优表.最优解

即甲、乙工段各需开工3天和2天，最低费用为7 000元.

表2－20

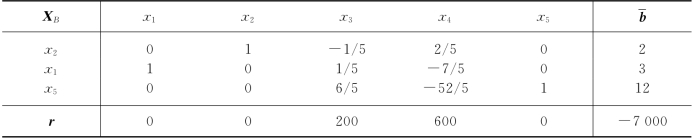
由表2－20知，最优基B＝（A.2，A.1，A.5），于是

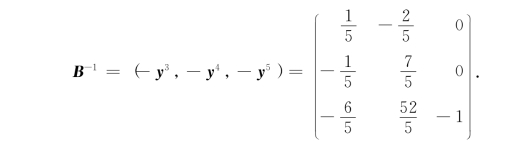
为使最优基保持不变，由式（2－24）知Δb1应满足下列条件：

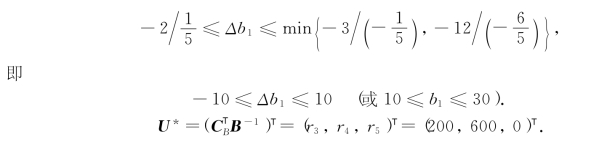
所以当b1∈［10，30］时，每吨A1类产品的合理成本为200元.

如果一个单位的A1产品的利润为220元，则显然将现在的b1＝20提高，对工厂是有利的，但是b1至多可提高到30.

应注意，在我们上面讨论的问题中，只有在保持B为最优基时，向量才是合理成本向量和影子价格向量.一般地，若B为线性规划

所相应的标准型线性规划的最优基，则称向量

为原有问题的影子价格向量，称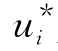为关于bi的影子价格.

例2－21　某公司下属两个工厂D1与D2，工厂D1生产产品Aj（产量为xj，j＝1，2），工厂D2生产产品Aj（产量为xj，j＝3，4）.这4种产品都需要耗费原材料B1与B2.现在原材料B1与B2分别有280与220.公司对两个工厂原材料的分配规划为：原材料B1给工厂D1为180、给工厂D2为100；原材料B2给工厂D1为140、给工厂D2为80.于是得到两个线性规划：

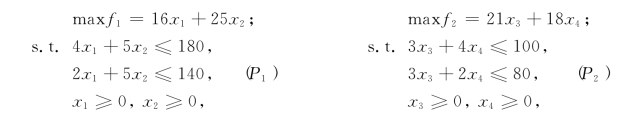
它们对应的标准型的最优单纯形表分别为表2－21和表2－22（其中xj，j＝5，6，7，8为松驰变量）.现在公司的决策部门准备对原材料的分配进行调整，以使总产值能够增加，请提供决策方案.

表2－21

表2－22