例6-17 (最优分配问题) 有一个仪表公司打算向它的3个营业区设立6家销售店,每个营业区至少设一家,所获利润如表6-14所示.问设立的6家销售店数应如何分配,可使总利润最大?
表6-14
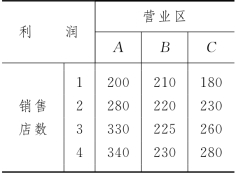
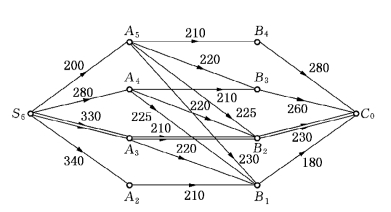
图6-27
解 作网络图D如图6-27所示.
顶点S6表示初始时公司拥有6家销售店待设置.顶点Ai表示在A区设立销售店后还剩有i家销售店未设立;顶点Bj表示在对A、B区设立销售店后还剩有j家销售店未设立;C0表示公司已将6家销售店设置完.边(S6,Ai)表示在A区设立6-i家销售店;边(Ai,Bj)表示在B区设立i-j家销售店;边(Bj,C0)表示在C区设立j家商店.图6-27中边旁的权为表6-14中相应参数.
于是,S6至C0的任一条路径表示一个具体的销售店的分配方案.例如S6A5B3C0指在A区设立1家销售店,在B区设立2家销售店,在C区设立3家销售店.我们的问题归结为在图D中求S6至C0的最长路径.
由算法可求出S6至C0的最长路径为S6A3B2C0,其长度为770.故最佳决策为:在A,B,C区分别设立3、1、2家销售店,可获得利润770.
例6-18 (货物装载问题) 现有一辆最大装载量b=5吨的卡车装载3种货物.已知3种货物单件重量和价值如表6-15所给.问卡车对各种货物装运多少,使卡车装载的货物总价值最大?
解 设第j种货物装载xj件(j=1,2,3),得整数规划模型:
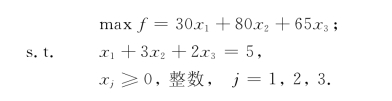
建立网络模型D=(V,E)如图6-28所示.
图D的顶点个数n=b+1=6.当V(D)的顶点vi及vk对应的下标差(k-i)恰等于j#货物单件重量aj时,则给有向边(vi,vk),且W(vi,vk)=cj.
表6-15

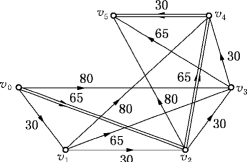
图6-28
显然,图D中任一条v0至v5的路径P对应了3种货物的一个装载方案:若权为cj的边在路径P中出现dj次,则j#货物装运dj件(xj=dj).路径的长度W(P)即为该方案所获得的价值f.
例如,在路径P=v0v1v3v4v5中,
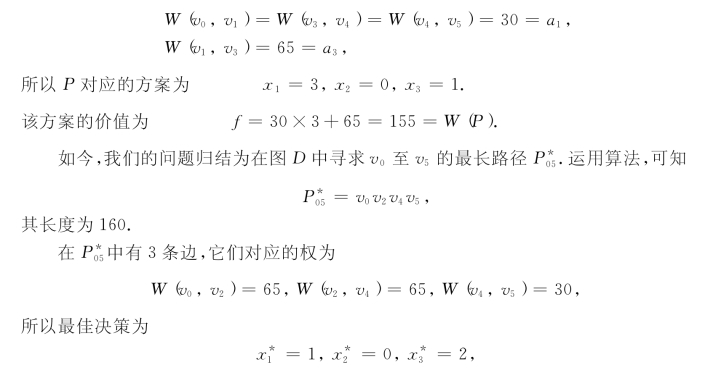
即1#货物装载1件,2#货物不装,3#货物装载2件,其总价值为160.
例6-19 (设备更新问题) 某公司明年年初(视为第一年,i=1)将对它的一辆已使用了2年的卡车(记作0#型)考虑5年内的更新问题.第i年年初购进的卡车视作i#型(i=1,…,5).现给定有关符号如下:
ri(t)——在第i年,一辆已使用了t年的卡车所能得到的收益;
ui(t)——在第i年,对一辆已使用了t年的卡车应花的维修费;
ci(t)——对j#型(j=0,1,…,5)卡车,使用t年,在第i年年初的更新费(i>j).
假设各种型号的卡车的有关信息如表6-16至表6-21所给.公司每年年初都面临卡车更新与否的决策问题.问公司从明年起,在5年内如何制定卡车的更新计划,使总的收益最大?
解 我们作iOt直角平面坐标系.点(i,t)意味着在第i年初卡车处在已使用t年的状态.
表6-16(https://www.daowen.com)

表6-17

表6-18

表6-19

表6-20

表6-21

点(i,t)至点(i+1,t+1)的有向边指这样的决策:在第i年年初,卡车已使用t年,现继续使用,则在第i+1年年初,卡车已使用t+1年.该有向边的权即相应决策的效益ri(t)-ui(t).
点(i,t)至点(i+1,1)的有向边指这样的决策:在第i年年初,卡车已使用t年,现进行更新,则在第i+1年年初,卡车处于使用1年的状态.该有向边的权即相应决策的收益为
![]()
于是,得网络图D如图6-29所示,其中点(7,3)为虚设点.点(6,i)至点(7,3)的有向边的权都为0(i=1,…,5,7).
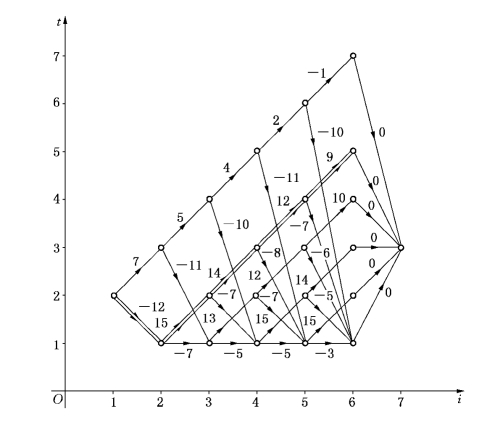
图6-29
在图6-29中,例如点(1,2)至点(2,3)有向边的权为
![]()
点(1,2)至点(2,1)有向边的权为
![]()
又如点(3,1)至点(4,1)有向边的权为
![]()
点(1,2)至点(7,3)的任一条路径代表一种卡车更新方案.
例如,路径(1,2)(2,1)(3,2)(4,3)(5,1)(6,1)(7,3)代表的卡车更新方案为:第1年年初时卡车已使用2年,更换新卡车,第2、第3年继续使用,第4年年初更换新卡车,使用一年,第5年年初更换新卡车,使用至年底.该路径的长度即为相应的卡车更新方案5年内的收益.
于是,本问题化为求一条点(1,2)至点(7,3)的最长路径P*问题.由网络图D可知:
![]()
其长度为38.所以,最佳决策为:第1年年初对一辆已使用2年的卡车进行更新,一直使用至第5年年末,总收益为38.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







