基于交通CPS的实验结果分析

本实验继续使用3.5.2 小节的合成数据集生成方式。为了测试算法应用于随时间不断演化的流式数据的性能，不同时间步时的数据集见表4.2。

表4.2　合成数据集描述

首先，为了测试聚类效果随聚类数k 变化的趋势，考虑了聚类数2～20变化时各个算法的聚类性能。

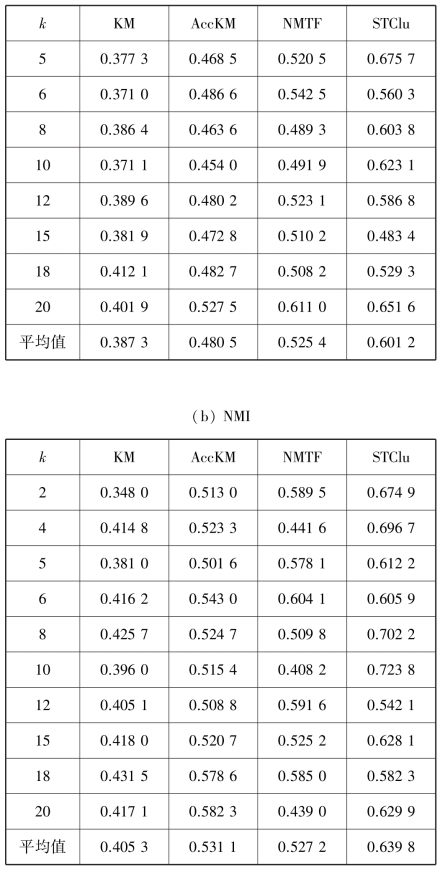
基于合成数据集的各算法的ACC 和NMI 见表4.3。通过表4.3 可以发现，算法STClu 因为考虑了历史信息的影响和历史信息与当前信息之间的关联关系，所以整体上优于其他3 种算法。AccKM 算法较之其他算法较优的原因是其考虑了历史信息的影响。NMTF 算法的聚类效果优于KM 算法的原因是因为不仅考虑数据的数据结构还考虑数据的特征结构。

表4.3　不同聚类数时，基于合成数据集的4 种算法聚类性能

续表

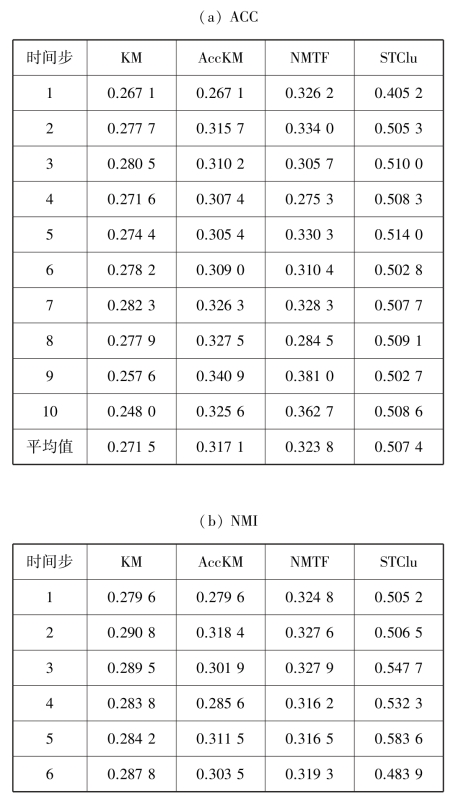
为测试4 种算法随时间变化的聚类性能，在不同的时间步上对算法的聚类性能进行测试。基于合成数据集的4 个算法在不同时间步上的ACC 和NMI 见表4.4。

表4.4　不同时间步时，基于合成数据集的4 种算法聚类性能

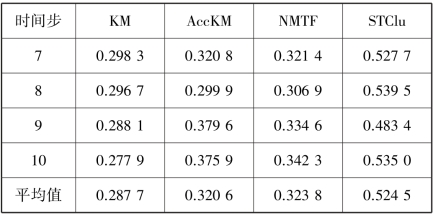
续表

(https://www.daowen.com)

通过表4.4 可以看出，STClu 算法整体优于其他3 种算法，NMTF 算法在大多数时间步优于AccKM 算法，AccKM 考虑了历史信息的影响，除第一步外，大多数时间步上优于KM 算法。

为了测试STClu 算法的适应性和鲁棒性，本节从聚类数目的变化和流式数据数目的变化两方面进行了测试，实验结果如图4.3 所示。从图4.3 的实验结果可以看出，算法STClu 的ACC 和NMI 有所变化，但是，都是在有限的范围内变化，并且这种变化也可能是受数据集本身的影响所导致的。

为了测试算法的效率，本节从聚类数目的增加和流式数据数目的增长两个方面进行了验证。

首先，聚类数k 在5～300 变化时，每一个时间步的流式数据数目为2 000，每一条流式数据包括1 024 个数据点，实验结果如图4.4 所示。其中，y⁃axis 为算法的平均处理时间，x⁃axis 为聚类数的变化。

其次，流式数据数目n 在50 ～2 000 变化时，每一条流式数据包括1 024个数据点，每一个时间步的聚类数目k＝32，实验结果如图4.5 所示。其中，y⁃axis 为算法的平均处理时间，x⁃axis 为流式数据数目的变化。

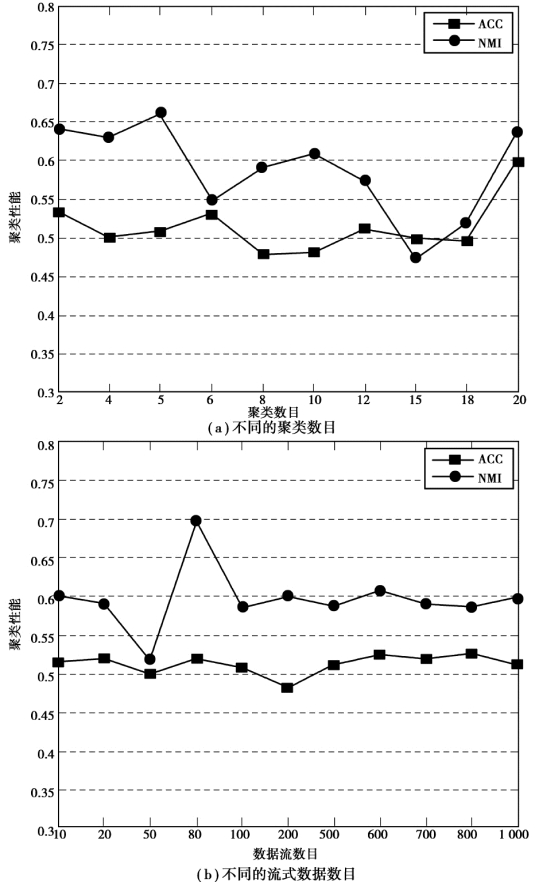
图4.3　STClu 算法的稳定性分析

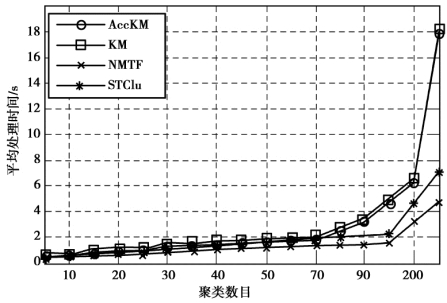
图4.4　当聚类数k 从5～300 时，4 种算法的平均处理时间比较

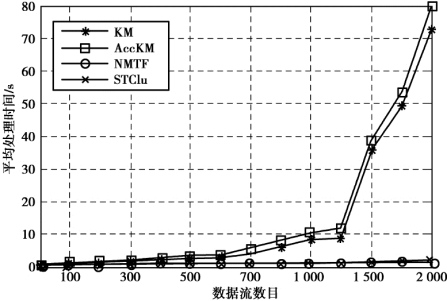
图4.5　当流式数据数n 从50～2 000 时，4 种算法的平均处理时间比较

通过图4.4 和图4.5 可以看出，随着聚类数的变化和流式数据数目的增长，各个算法的执行时间均有所增长。但是，算法STClu 与NMFT 算法的处理时间增长速度较之KM 和AccKM 算法比较缓慢。其原因在于，基于矩阵分解的STClu 和NMTF 算法在处理高维数据的聚类时进行了低秩近似处理。因为算法STClu 嵌入了先验信息，所以其处理时间略高于NMFT 算法。但是，从平均处理时间的整体趋势可以发现，两者的增长趋势基本一致。