分枝定界法：整数规划模型的求解方法

尽管已经有许多学者研究出整数规划的多种求解方法，但至今比较成功的算法是Land和Doig提出的经过Dakin修正的分枝定界法。这种算法的最大优点就是不但可以求解纯整数规划问题，也可以求解混合整数规划问题。

分枝定界法的基本步骤如下：

第一步：先不考虑整数约束条件，对一般情况的线性规划问题用单纯形法或对偶单纯形法求解。如果求出的最优解满足整数规划问题的所有整数约束条件，那么这个最优解就是整数规划问题的最优解；如果有一个或多个整数约束条件没有被满足，转到第二步。

第二步：任意选择一个应该是整数而不是整数解的变量xk，设它的非整数解是bk，同时设bk对应的整数位是[bk]，现在将原问题分成两枝：一枝是在原问题的基础上，增加约束条件xk≤[bk]；另一枝是在原问题的基础上，增加约束条件xk≥[bk]+1，这样就构成了两个新的线性规划问题的子问题。

第三步：按照第3.3节对偶单纯形法扩展应用的思路，分别对分枝后的两个新线性规划子问题继续求解。若新的解不满足原问题整数约束，再按第二步进行新的分枝，直到满足下面的情况为止：

（1）该分枝上的子问题没有最优解，此时如果再增加一个约束条件也不可能有最优解。

（2）已经求出了一个不违反任何约束的解，此时再增加约束条件，即使仍然可以求出整数解，但目标函数值也不可能变得更优。

（3）此子问题的目标函数值不优于任何一个不违反整数约束的另一个子问题的目标函数值，因为此时如果再对此子问题进行分枝，新的子问题由于增加了约束条件，其目标函数值也不会优于原来的子问题，更不会优于不违反整数约束的那个子问题，所以没必要继续再分枝。

下面通过例题具体说明分枝定界法的求解步骤。

例7.3　求解下列整数规划模型：

解　现在暂不考虑整数约束，用单纯形法求解，得到最优单纯形表7.2：

表7.2(https://www.daowen.com)

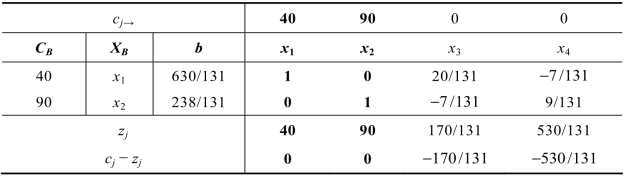
表7.2对应最优解的基变量取值约为x1=4.81，x2=1.82，目标函数值z0=356.2，但x1、x2均不符合整数约束。这里选择x1=4.81进行分枝：4.81对应的整数位是4，现在分成两枝，一枝是在原问题基础上，增加约束条件x1≤4；另一枝是在原问题基础上，增加约束条件x1≥5。为了描述方便，现在构造一个树形分枝图，向下分成左右两枝，如图7.3所示。

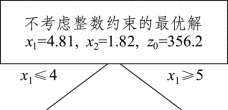
图7.3

按照第3.3节对偶单纯形法扩展应用的思路，把图7.3的左枝x1≤4加上松弛变量x5化为x1+x5=4，把其系数补加到表7.2中去，继续用对偶单纯形法求解，得到的最优解为x1=4，x2=2.1，目标函数值z1=349。同样，把图7.3的右枝x1≥5减去多余变量x5化为x1-x5＝4，把其系数补加到表7.2中去，继续用对偶单纯形法求解，得到的最优解为x1=5，x2=1.57，目标函数值z2=341，把求出的结果扩充到图7.3中，如图7.4所示：

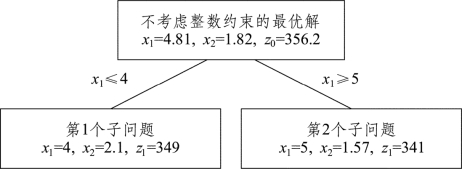
图7.4

对图7.4继续按照以上思路进行分枝，再把新的约束加到上一过程的最优单纯形表中，然后求解，逐步进行下去，最终的结果如图7.5所示。

在图7.5中，第3个子问题不分枝的原因是满足停止分枝的第（2）种情况；第4个子问题不分枝的原因是满足停止分枝的第（3）种情况；第5个子问题不分枝的原因是满足停止分枝的第（3）种情况；第6个子问题不分枝的原因是满足停止分枝的第（1）种情况。这样，全部分枝都终止延伸，求得最优解为x1=4，x2=2，目标函数值z0=340。

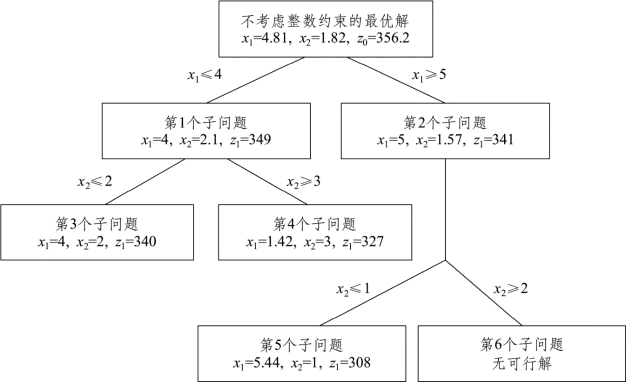
图7.5