第6章　岩盐溶腔稳定性

6.1　溶腔稳定性的主要影响因素

6.1.1　地应力的大小及方向对溶腔稳定性的影响

位于一定地应力环境中的岩体，相对地处于平衡状态。由于水溶开采形成岩盐溶腔，破坏了岩体原始受力状态而失去平衡，引起岩体产生变形。同时，地应力还严密控制着岩体的本构特征，其相关性表现为：

①影响岩体的承载能力　大量岩体的三轴试验结果表明，其抗压强度随围压增大而增高。对赋存于一定地应力环境中的岩体来说，地应力对岩体形成的围压越大，其承载能力越大。

②影响岩体变形破坏机制　岩体力学试验结果表明，许多在低围压下呈脆性破坏的岩体，在高围压下呈剪塑性变形。这种变形破坏机制的变化，揭示着岩体赋存的地应力条件不同，岩体的本构法则不同。

③影响岩体中应力传播法则　虽然岩体具有不连续性，为非连续介质。但是，由于岩块间存在的摩擦作用，赋存于高应力区的岩体，在地应力形成的高围压作用下，则变为具有连续介质特征的岩体，即地应力可以使不连续变形的岩体转化为连续变形的岩体，从而使岩体中应力传播具连续介质的特征。

地应力状态影响工程岩体的稳定性，主要是岩体的天然应力状态，包括自重应力和构造应力，以及地下工程形状对围岩应力重新分布的影响。

地应力是引起围岩变形、破坏的根本作用力，原岩体中主应力的大小和方向不同，对溶腔的作用力也不同，因而直接影响着围岩压力。

通常，地应力随深度的增加而增加，所以溶腔埋深越大，围岩压力一般也就越大。

地应力方向对围岩压力也有显著影响。对连通井组而言，存在溶腔的长轴与短轴方向。当溶腔长轴方向与最大主应力的方向垂直时，围岩压力就大，平行时围岩压力就小。这是因为溶腔长轴方向不同，原岩应力对其作用不同。前者溶腔横截面受到的作用力大，而后者受到的作用力小。因此，溶腔长轴的最优方向，应与最大主应力方向一致。

6.1.2　岩体的物理力学性质对溶腔稳定性的影响

（1）岩体特性的影响

岩性是影响地下工程岩体稳定的最基本因素，是物质基础。由于矿物组成、岩石结构构造的不同，不同岩石的物理力学性质差别很大。以岩石特性可将围岩分为塑性围岩和脆性围岩两大类。塑性围岩，主要包括各类粘土质岩石、岩盐、破碎松散岩石以及某些易于吸水膨胀岩石，通常具有风化速度快、力学强度低以及遇水易于软化、崩解等不良性质，而对地下工程岩体稳定性最不利。脆性围岩主要包括各类坚硬及半坚硬岩体；由于岩石本身的强度远高于结构面的强度，故这类围岩的强度主要取决于岩体结构，岩性本身的影响不十分显著。

（2）岩体结构的影响

岩体结构对围岩变形破坏起着决定性作用，碎裂结构岩体的稳定性最差，薄层状结构岩体次之，而厚层状及块体状岩体则具有很高的稳定性。对于脆性的厚层状及块体状结构的岩体，其强度主要受较弱结构面的发育和分布特点所控制。结构面对这类围岩的稳定性影响，不仅决定于结构面本身的特征，还与结构面的组合关系，以及结构面和临空面的切割关系有密切联系。一般情况下，只有当结构面的组合使围岩内可能出现有利于塌落或滑动的分离体，且尺寸小于硐垮时，这类围岩才有局部失稳的可能。

当结构面强度远小于结构体强度时，结构面对围岩压力的影响就显得十分重要。通常岩体破坏首先从弱面开始，这是围岩压力在节理、破碎带、断层和褶皱区表现显著的重要原因。由于层状岩体具有定向弱面，所以层状岩体的走向和倾角也与围岩压力密切相关。

6.1.3　地下水对溶腔稳定性的影响

地下水在围岩稳定中主要有两方面不良的作用：一方面是对围岩特性的影响；另一方面为渗压的作用。

岩体空隙中水的存在形式有两种：吸着水（束缚水）；重力水（自由水）。

吸着水因静电引力而吸附在矿物颗粒表面，在相对湿度较大时，水在矿物颗粒表面形成水膜，故又称薄膜水。薄膜水对岩体的力学性能影响表现为水的联结作用（水胶作用）、水的润滑作用和水楔作用3个方面。岩体的软化、膨胀、崩解无不与之有关。矿物按其与水作用的特征，可分为亲水性矿物和憎水性矿物。岩块中亲水性矿物（和可溶性矿物）愈多，在水的作用下其力学性能愈不稳定。这种岩块在含水量低时，一般强度较高，压缩性小，呈脆性破坏，具弹性介质特征；如含水量高时，则强度减小，呈塑性破坏特征。

研究表明，吸着水的软化作用，不仅存在于低围压条件下，而且存在于较高的围压条件下。岩体中水对岩石的软化作用不仅表现在抗压、抗拉强度上，亦表现在变形特征上。

自由水不受矿物表面吸着力控制，它的运动主要靠重力作用，其运动速度μ取决于岩体的渗透系数K及水力梯度I，即

式中　H——在渗透途径长L内的水位差。

自由水所形成的压力бW主要决定于水的密度ρw及水头H，即

бW＝ρw·H

自由水对岩体除具吸着水同样的力学作用即使岩石软化、膨胀、崩解外，还由于孔隙压力作用，抵消外界作用的正压力，而使岩块抗剪强度降低。如岩体中软弱结构面上受到静水压力作用，将会降低其抗滑能力，从而导致岩体失稳；或由于工程岩体开挖，地下水从溶腔排出，或涌入溶腔均能形成动水压力，对岩盐溶腔围岩的稳定性影响极大。

岩石中渗透水在其流动过程中有时可将岩块中可溶物质溶解带走，有时由于其黏度和动力作用也可将岩块内小颗粒矿物带走，从而使岩块强度降低，变形加大。前者称为溶解作用，后者称为潜蚀作用，随着时间的增长，其影响更加明显。

综上所述，地下水是影响岩体力学性质和力学作用的主要因素之一，在岩体力学作用中是一种动力作用因素。工程岩体中地下水的赋存、活动状况，既影响围岩的应力状态，又影响围岩的强度。结构面中的空隙水压力的增大能减少结构面上的有效正应力，因而降低岩体沿结构面的抗滑强度；地下水对软弱夹层软化、泥化，对一些特殊岩层产生膨胀、崩解和溶解等，则降低岩体的强度而影响围岩的稳定性。因此，在研究溶腔稳定性控制时，必须充分重视水的力学效应，特别应控制溶腔顶板岩层裂隙带水的渗透作用。

6.1.4　地质构造对溶腔稳定性的影响

岩体稳定与否的根本原因应该从岩体内部去寻找。因此，对工程所在岩体进行地质调查，掌握该地的地质情况，在此基础上进行岩体稳定分析，是地学工作所必须遵循的工作方法。

影响溶腔围岩稳定性的因素除地应力、岩体物理力学性质、地下水之外，地质构造也是一个重要的因素。

（1）地层产状对溶腔围岩稳定性的影响

岩层倾角对围岩稳定性具有很大的影响，一般来说，水平岩层对稳定性最有利，倾斜岩层次之，竖直地层最差。

（2）褶皱对围岩稳定性的影响

沿背斜轴部，在中和线以上张裂隙发育，中和线以下地层本身形成一个拱，有利于围岩稳定。中和线不易直接判定，因此一般可选在两翼，因两翼岩层完整性要好些。向斜轴部较破碎，加之两边层面往轴部倾斜，易成为汇水和地下水主流之处，故溶腔应避开向斜轴而选在翼部。从向斜轴部岩层没有拱的作用以及汇水的这两点来看，向斜比背斜条件要差些。

（3）断层和破碎带对岩体稳定的影响

断层是一种特殊的结构面，当断层宽度很小又不夹泥，则它对岩体稳定影响同一般节理差不多。当夹泥，则其影响作用很大。若又是断层破碎带又夹泥，则是最危险的。

断层破碎带、岩脉破碎带、褶皱轴部有时也形成破碎带，它们本身就是许多分离体，溶腔应尽量避免设在这些地方，避不开则应尽可能垂直它，以使不稳定的范围减低到最小的限度。

6.1.5　开采层厚度对溶腔稳定性的影响

在一定的地质条件下，开采层厚度（岩盐层厚度）是影响岩盐溶腔上覆岩层破坏状况的最重要因素之一。一般地，开采层厚度超大，必然导致岩盐溶腔上覆岩层破坏越严重。矿山开采的理论和实践均表明，在其他条件一定的情况下，溶腔顶板下沉量及上覆岩层的移动和变形均与开采厚度成正比，开采厚度越大，冒落带、导水裂隙带高度越大，上覆岩层移动变形值也越大，岩层移动过程表现得越剧烈，溶腔围岩矿压显现也越严重；反之，开采厚度越低，同样位置的老顶取得平衡的机会越大，顶板活动越缓和，越利于溶腔的稳定。

6.2　岩盐溶腔稳定性突变模型

在自然界，特别是地学，不连续变化的现象非常多，如地震、火山喷发、地磁场倒转、煤瓦斯突出、岩爆等。地质现象的不连续性和地质事件的突然性是至今阻碍着地球科学定量化的重要原因之一。近年来，国内外许多学者试图利用突变理论来解释和解决地球科学中的不连续现象和问题［109］。

作者采用突变理论研究岩盐单井溶腔顶板、连通井顶板稳定性及井组间矿柱失稳的临界条件及突变时的突跳和能量释放，以深入了解顶板岩体运动过程和矿柱失稳的发展过程，为溶腔稳定性控制提供理论基础。

6.2.1　单溶腔顶板大变形失稳突变模型

岩盐溶腔由于常处于较大埋深（600～2 000 m）、顶板岩层自身强度低、变形模量小、有高的地应力作用，故表现出非线性和大变形特征。又因溶腔多呈倒锥形，所以本研究把溶腔顶板简化为周边固支的圆板，半径为r0，厚度为t，且在上面作用有顶板岩层自重及上覆岩层的作用力q，p为溶腔内液体的压力，如图6.1所示。

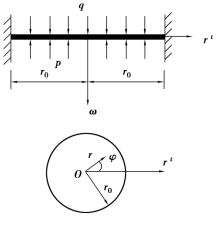
图6.1　单腔顶板简化力学模型

本模型的边界条件为

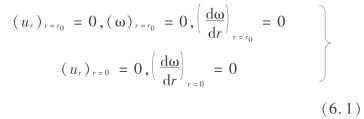
式中　ur——径向位移；

　ω——挠度。

由文献［110］得板的挠曲面方程为

式中　D——板的抗挠刚度。

设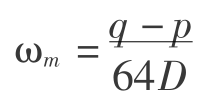ω＝q- p，则ω为板中心的最大挠度，所以

m 64D m

根据边界条件式（6.1），可将径向位移ur用级数形式表示为［111］

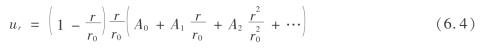
可近似为

由弹性力学的变分法［112］可得

式中　a1，a2——常数。

把式（6.6）代入式（6.5）得

顶板系统岩层系统的势能∏可表示为

式中　U——岩层的变形势能；

　W——外力所做的功。

因本模型为大变形板模型，岩层的变形势能应该包括岩层弯曲形变的势能及相应于中面应变的势能，故

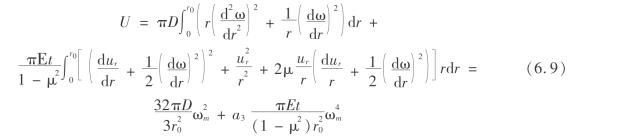
式中　μ——顶板岩层的泊松比；

　E——顶板岩层的弹性模量；

　a3——常数。

外力功W应包括顶板岩层自重和上覆岩层的作用力q在轴向和径向所做的功和水压力p在轴向和径向所做的功，则

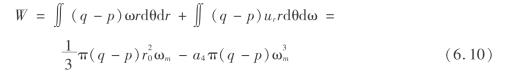
式中　a4——常数。

把式（6.9）、式（6.10）代入式（6.8）得溶腔顶板岩层系统的势函数∏为

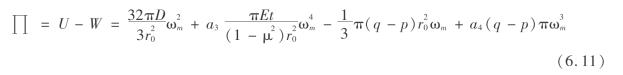
设

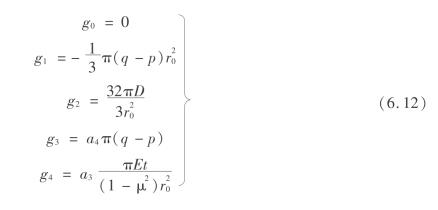
则

令

且设

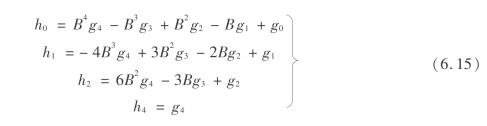
则

令

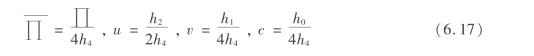
则

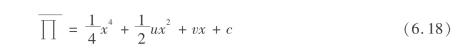
本系统的平衡曲面的方程为［75］

分歧点集所满足的方程为

所以本系统失稳的必要条件为

即

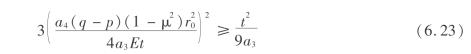
即为溶腔顶板岩层失稳的必要条件。所以当顶板岩层厚度越薄、弹性模量越小、顶板跨距越大及（q- p）越大越容易引起溶腔顶板岩层失稳。

6.2.2　连通井溶腔顶板失稳临界突变分析

（1）连通井溶腔顶板力学模型

已有研究表明，连通井组溶腔悬露顶板近似为矩形，其长度远大于宽度，可简化为梁。

如图6.2所示，溶腔顶板部分长为L，水平宽度取单位长度，平均厚度为h，L≫h，岩体弹性模量为E，顶板岩层自重及其上履岩层的力简化为均布力q，岩梁两端受自重侧压压力及水平构造应力的综合作用力N，均布力P为溶腔内液体的支撑力。

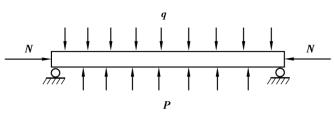
图6.2　连通顶板简化力学模型

梁的轴线挠曲线f可用傅氏级数展开为

在二级近似的条件下，f（s）可表示为

式中　s——弧长；

　f（s）——挠度；

　Y——轴线中点的挠度。梁结构的总势能应由弯曲应变能和载荷在相应位移上所做的功组成，因此梁结构的势函数为

式中　U——梁的应变能；

　W1——水平力N所做的功；

　W2——垂直力q所做的功；

　W3——液体支撑力P所做的功。假设梁的变形服从平截面假设，即应变分布应服从

式中　R——中性线的曲率半径；

　H——截面上的点距中性线的距离。

因此，有

截面上的力矩为

令

即梁的惯性矩。

则

梁的应变能为

把式（6.29）代入式（6.32）得

式中　K——梁的曲率。

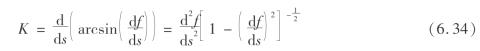
将式（6.34）代入式（6.33）得

在水平力的作用下，梁的水平方向上的缩短量为

所以水平力N所做的功为

垂直均布力q所做的功为

溶腔液体支承力P所做的功为

将式（6.35）、（6.37）、（6.38）、（6.39）代入式（6.26）得梁的势函数为

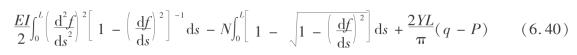
（2）连通井溶腔顶板失稳的尖点突变模型

对式（6.40）被积函数泰勒级数展开，整理可得梁结构势函数的近似表达式为

设

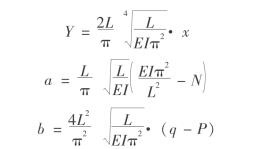
则

所以，平衡曲面M的方程为

分歧点集所满足的方程为

即

讨论：

①如图6.3所示，A点是系统稳定平衡的临界点，满足方程Δ＝0，即

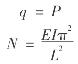
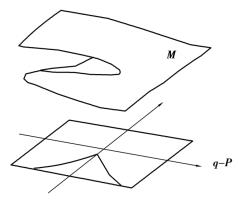
图6.3　梁结构的突变模型

因为只有当a≤0时才有跨越分歧集的可能，故得系统发生突跳的必要条件为

即

所以顶板岩盐的弹性模量E越小，采场跨距L越大，或者水平构造应力及自重侧压压力越大，系统就越容易发生突变，导致顶板的失稳。

②根据突变理论，当控制点跨越分歧点时，才会发生突变。此时有两种情况b＞0或b＜0。当b＜0时，即q- P＜0，这种情况在现实条件中基本不存在，所以只有b＞0的情况存在，则q- P＞0，即q＞P。

所以溶腔顶板失稳的充要条件为

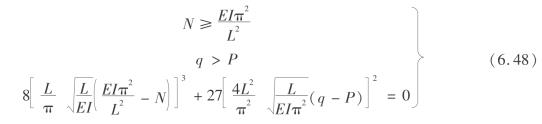
因此，连通井溶腔顶板稳定性不仅与顶板所受垂直力和水平力的联合作用有关，而且与溶腔顶板跨距的增大及顶板系统的内部特征如顶板岩盐的弹性模量有密切的关系。水平应力越大、顶板岩层弹性模量越小、溶腔跨距越大，越容易引起溶腔顶板突跳破坏。

6.2.3　井组溶腔间矿柱稳定性突变模型

井组间矿柱的稳定性，是保障井组正常生产的关键。矿柱留设太大，会浪费大量岩盐资源，影响采区的开采率。而矿柱留设太小，会突跳失稳破坏，从而导致顶板大面积来压，致使井组报废。所以研究井组间矿柱的稳定性具有十分重要的意义。

（1）力学模型

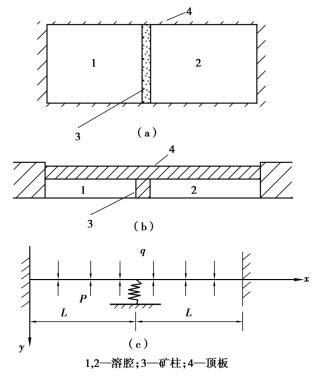
假设矿柱对称分布，且其宽度远小于溶腔宽度，可将顶板岩层视为梁。为简化分析，设未采岩盐为刚性，梁是固支的，将矿柱视为一维柱体，并且梁为坚硬顶板，故在变形过程中始终保持弹性且不发生破坏，矿柱对顶板的支撑力视为集中力，顶板岩层自重及其上覆岩层的力简化为均布力q，P为溶腔内液体的压力，如图6.4所示。

设矿柱的本构关系具有软化性质的非线性关系，如图6.5所示，其本构关系为［113］

式中　u——矿柱压缩量；

　λ——矿柱的初始刚度；

　u0——峰值荷载对应的变形值。

梁的变形是弹性的，设在中点处梁的变形和矿柱的变形之和为b，则梁在中点处挠度为b- u，根据边界条件，可把梁的挠曲线方程写为［114］

(www.daowen.com)

图6.4　简化力学模型

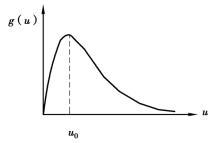
图6.5　矿柱的应力—应变曲线

式中　s——弧长；

　f（s）——挠度。

梁和矿柱构成的系统的总势能V应由梁的弯曲应变能、煤柱的压缩变形能及外力的功所组成。由于梁为坚硬顶板，所以梁—矿柱系统总势能可近似写为

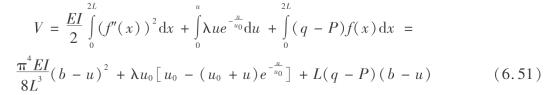
式中　E——梁的弹性模量；

　I——梁的惯性矩。

（2）突变模型

平衡曲面M为

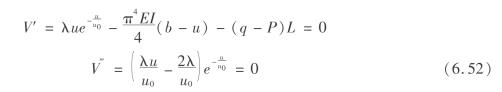
所以尖点处有

将平衡曲面展开为尖点处状态变量u1处的幂级数，并截取至前3次项得

把式（6.52）、式（6.53）代入式（6.54），并令

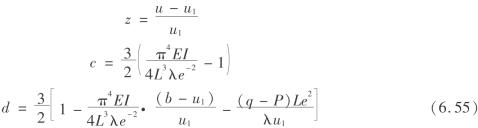
则式（6.55）变为

所以分歧点集所满足的方程为

显然只有c≤0时，系统才能跨越分叉集发生突变，即

即

因此梁—矿柱失稳的必要条件取决于系统内部特性，当矿柱的软化特性越强（λe2越大）、梁的弹性模量越小、跨距越大，越容易突变。

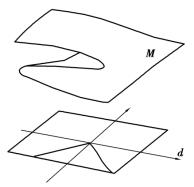
图6.6　梁结构的突变模型

由图6.6可知，当系统跨越分叉集左右支时才可能发生系统的突跳。但在跨越分叉集的右支（d＞0）时，系统的突变仅是系统的数学结构（平衡整个数和稳定性）有突变，而状态变量z没有跳跃。矿柱失稳时，其变形一般会瞬时增大，即对应于跨越分叉集左支（d＜0）的情况。所以

所以矿柱失稳的充要力学条件为

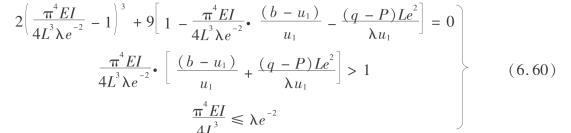
（3）矿柱突跳失稳的释能机制

当c＝0时，方程式（6.56）有三重零根；当c＜0时有三个实根。有

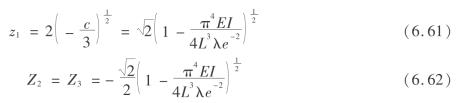
于是跨越分叉集时状态变量发生突跳量（见图6.7）为

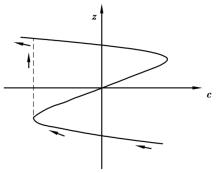
图6.7　跨越分叉集时状态变量z的突跳

所以矿柱失稳前后变形的突跳量为

由式（6.64）可知，矿柱变形突跳量仅与系统的内在特性有关。

将梁—矿柱的系统函数在尖点u1处泰勒展开，并把式（6.55）代入得

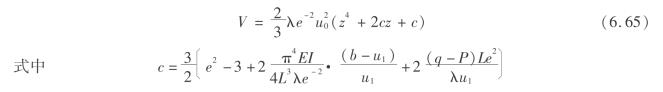
矿柱失稳突跳前后的能量差为

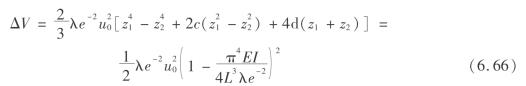
由式（6.66）可知，突跳所释放的能量仅与系统的内在特性有关。

6.3　溶腔储气库运营期稳定性综合评价模型

作者应用安全系统科学理论建立盐岩地下储气库运营期稳定性的多层次、多指标综合评价体系。采用可拓法和模糊综合评价法对同一地下储气库进行评价，以检验评价体系的可靠性。

6.3.1　体系设计及评价指标

充分考虑盐岩地下储气库运营期稳定性的内在特征、外界环境构成要素，将盐岩地下储气库运营期稳定性评价分解为若干个评价层来考虑，采用自下而上的层次设计方法，基于相关理论成果，结合工程实际，合理、有效地确定其下层各评价子项目，形成一个包含多个评价子项目的多层次评价系统，由底层到中层再到顶层进行深入细致的研究。顶层为盐岩地下储气库运营期稳定性，称为目标层。中间层为描述盐岩地下储气库状态的项目，称为描述层。底层为盐岩地下储气库运营期稳定性评价的指标及其指标的表征量，称为指标层。评价体系及评价指标如图6.8所示。

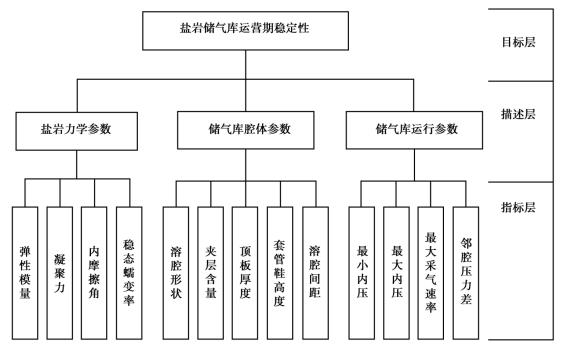
图6.8　盐岩地下储气库运营期稳定性评价体系及评价指标

6.3.2　稳定性等级标准及指标评分方法

结合相关行业安全等级分类，将盐岩地下储气库运营期稳定性分为5个评价等级：I级为不稳定、Ⅱ级为基本稳定、Ⅲ级为较稳定、Ⅳ级为稳定、Ⅴ级为很稳定。以百分制分别对应分值为：Ⅰ级：［0，60］；Ⅱ级：［60，70］；Ⅲ级：［70，80］；Ⅳ级：［80，90］；Ⅴ级：［90，100］。

为减小主观性，不采用专家打分的方式，而主要根据试验和数值模拟结果构建各参数的评分模型。

（1）盐岩力学参数评分模型

根据中国科学院武汉岩土力学研究所对云应和金坛盐矿盐样进行的单轴、三轴压缩和蠕变试验结果［10-11］，构建盐岩力学参数各指标的评分模型如表6.1所示。

表6.1　盐岩力学参数各指标评分模型

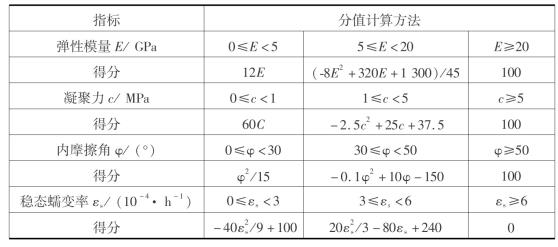
（2）储气库腔体参数评分模型

应用FLAC3D模拟计算储气库腔体流变30年后的体积收敛率（ΔV/V），规定溶腔形状指标得分为100（1-ΔV/V）。数值模拟表明，刚度大于盐岩而流变能力小于盐岩的泥岩夹层对储气库溶腔具有抑制变形的作用，但夹层含量太高，会影响储气库的密闭性和增加水溶建腔难度。盐岩具有良好的蠕变特性，预留一定厚度的顶板盐岩层，可以削弱溶腔变形对上部岩层及地表的影响，美国能源部规定回采厚度和溶腔最大直径之比为10，荷兰享格勒地区规定顶板厚度仅为5 m［12］。为防止套管由于盐岩蠕变承受较大的拉应力而破坏，套管鞋应距腔顶一定的距离，由套管钢材屈服强度和弹性模量计算其所能承受的应变变形，根据流变模拟结果确定最小套管鞋高度。对于储气库群，溶腔间距太大会浪费盐岩资源，间距太小则可能发生失稳破坏，假设储气库运行对围岩造成的影响范围分为塑性破坏区、中等程度扰动区和轻微扰动区厚度相同的3部分，为保证单个腔体互不影响，根据数值模拟的塑性区半径，确定溶腔安全间距，设安全系数r3为溶腔间距和溶腔直径之比，德国一般取r3＝1.5～3.0，美国一般取r3＝1.75～2.5。综合以上分析，并结合我国多为薄层状盐岩的实际，储气库腔体参数各指标评分模型见表6.2。

表6.2　储气库腔体参数指标评分模型

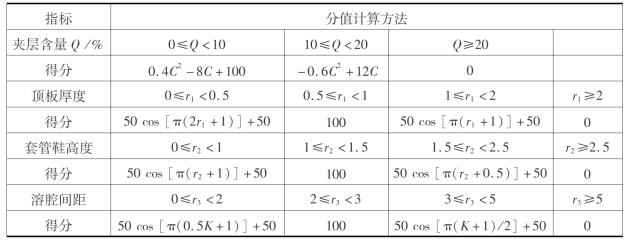
注：r1为顶板厚度和溶腔直径比值；r2为套管鞋实际高度与模拟高度比值，r3为溶腔间距和溶腔直径之比。

（3）储气库运行参数评分模型

储气库运行5年后体积收缩率应控制在5%以内，最大、最小内压比值范围是2∶1～6∶1，据此确定最小内压与最大内压［13］。储气库一年注采气周期下体积应变不应超过3%［14］，由此计算储气库最大采气降压速率。储气库多采用并联操作，即任意时刻邻腔压力差均为0，最有利于储气库稳定。综合以上分析，储气库运行参数各指标评分模型见表6.3。

表6.3　储气库运行参数指标评分模型

续表

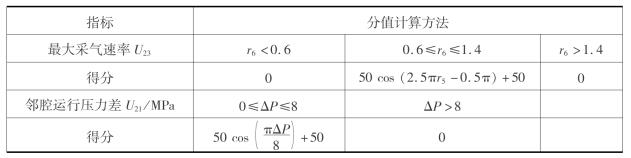
注：r4、r5、r6分别为储气库最小内压、最大内压和最大采气速率的运行值与模拟值之比；ΔP为邻储气库动态运行压力差。

6.3.3　评价等级对应指标的量值

根据以上评分标准，可以计算出5个评价等级的对应指标量值，见表6.4—表6.6。

由于表6.4—表6.6中各指标单位不统一，采用极差法对数据进行无量纲化处理，对数值越大越有利于稳定的指标，采用式（6.67）进行计算为

对数值越小越有利于稳定的指标，采用式（6.68）进行计算为

式中 X′ij——极差化后的数据；

Xij——原始数据；

Ximax、Ximin——第i行数据的最大值与最小值。

表6.4　各评价等级盐岩力学参数指标量值范围

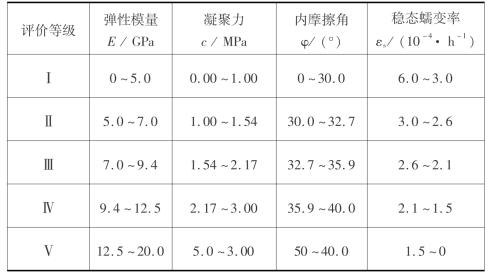
表6.5　各评价等级岩储气库腔体参数指标量值范围

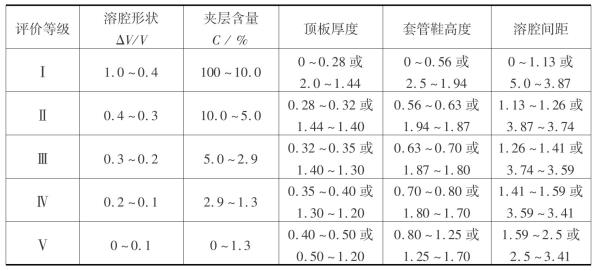
表6.6　各评价等级岩储气库运行参数指标量值范围

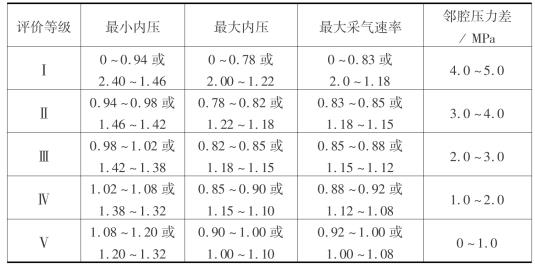
表6.4—表6.6中各指标无量纲化处理后，结果如表6.7—表6.9所示。

表6.7　无量纲化后各评价等级盐岩力学参数指标量值范围

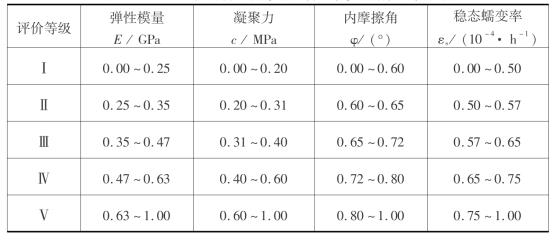
表6.8　无量纲化后各评价等级岩储气库腔体参数指标量值范围

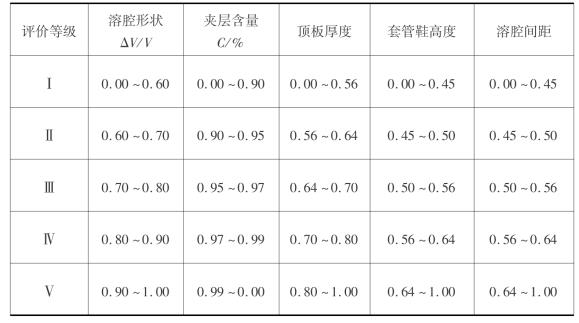
表6.9　无量纲化后各评价等级岩储气库运行参数指标量值范围

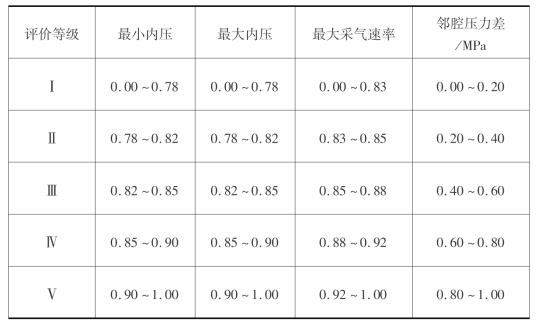
6.3.4　确定评价指标权重

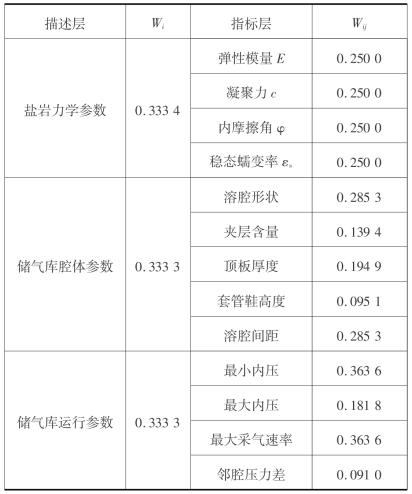
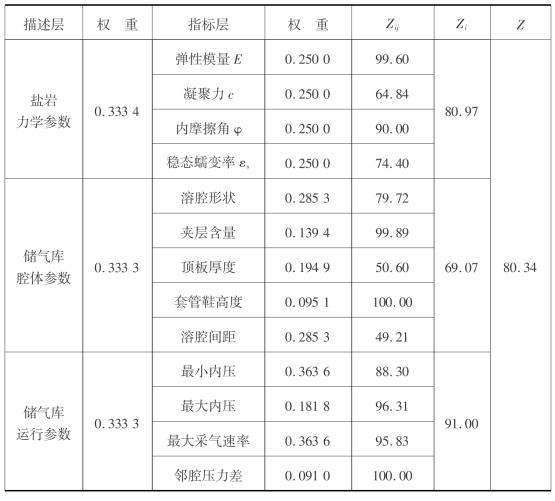
根据国外储气库建设经验和盐岩专家的建议［5，11］，采用AHP对描述层中盐岩力学参数、储气库腔体参数和储气库运行参数进行两两比较，构建判断矩阵M。利用Matlab软件的［V，D］＝eig（M）命令确定指标权重W，并进行一致性检验。同理确定指标层中各子指标在描述层中的权重，计算结果详见表6.10。

表6.10　指标权重取值

6.4　金坛西1储气库稳定性可拓法评价

基于物元的可拓法可以解决岩体工程稳定性评价过程中常见的矛盾相容、定量与定性共存等问题，得到了较为广泛的应用。

6.4.1　可拓法及评价步骤

可拓法是基于物元的评价方法，物元是其逻辑细胞。其评价步骤如下：

1）确定经典域

物元表示为

式中　N——事物的名称；

　C——特征；

　V——量值。

事物可以有n个特征c1，c2，…，cn和相应的量值v1，v2，…，vn。

经典域为物元中V的量值范围。

2）确定节域

节域表示为

式中　P——全部评价等级；

　Vp＝（api，bpi），（i＝1，2，3，…，n）——评价指标Ci在P条件下所取的量值范围。

3）确定待评物元

待评物元表示为

式中　N——待评对象；

　Ci——评价指标，（i＝1，2，3，…，n）；

　Vi——对应评价指标的取值。

4）计算单指标关联度

单指标关联度指待评价对象的第i个（i＝1，2，3，…，n）指标关于分类等级j（j＝1，2，3，4，…，m）的关联度，用式（6.72）—式（6.74）计算。

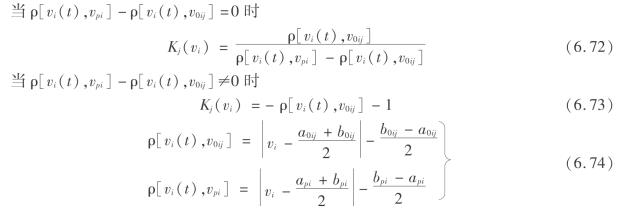
式中　K——单指标关联度；

　（a0ij，b0ij）（j＝1，2，3，4，…，m，m为评价等级）——评价指标Ci在所有条件下的量值范围。

5）计算多指标综合关联度

多指标综合关联度表征评价对象关于各评价等级的归属程度，可计算为

式中　j＝1，2，3，…，m；

αi——指标Ci的权重系数，权重系数之和必须等于1。

6）确定评价等级和级别变量特征值

在Kj（N）中，最大的majx［Kj（N）］所属的稳定性等级j即为待评价对象的稳定性等级。

待评价对象级别变量特征值可计算为

式中，K′j（N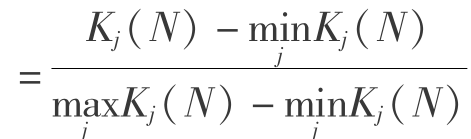），其中j＝1，2，3，…，m。

6.4.2　金坛西1储气库运营期稳定性待评物元

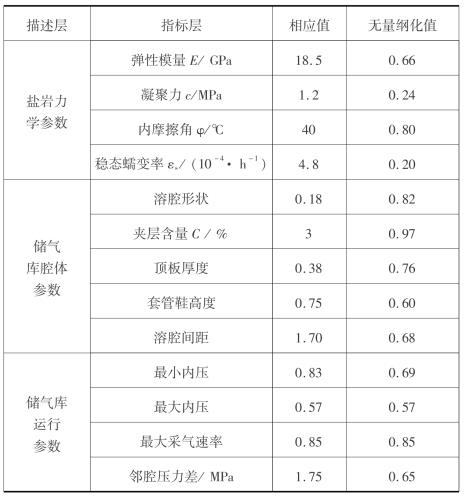
金坛西1储气库为我国最早的4个盐岩地下储气库之一，目前已经安全运营3年，储库稳定。其盐岩力学参数、储气库库腔体参数和运行参数详见表6.11。表中的无量纲化值即为西1储气库稳定性待评物元。

表6.11　运营期西1储气库稳定性评价指标取值

6.4.3　西1储气库可拓法评价及结果

西1储气库稳定性评价可拓评价由两部分组成：描述层和目标层可拓评价，描述层可拓评价是目标层可拓评价的前提和基础。

（1）描述层可拓评价

应用编制的可拓法评价计算程序，进行可拓法评价的4、5、6步，西1储气库描述层可拓评价过程及评价结果见表6.12—表6.14。

表6.12　盐岩力学参数可拓评价计算结果

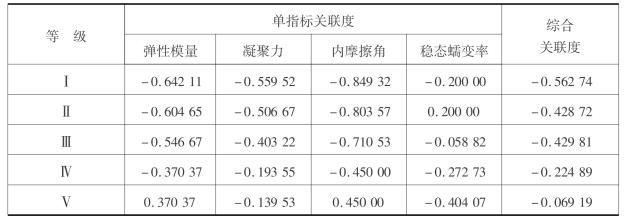
注：弹性模量、凝聚力、内摩擦角、稳态蠕变率权重分别为0.25、0.25、0.25、0.25；级别变量特征值为4.187。

表6.13　储气库腔体参数可拓评价计算结果

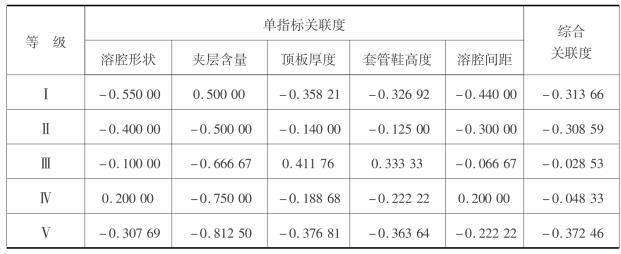
注：溶腔形状、夹层含量、顶板厚度、套管鞋高度、溶腔间距的权重分别为0.285 3、0.139 4、0.194 9、0.095 1、0.285 3；级别变量特征值为3.180。

表6.14　储气库运行参数可拓评价计算结果

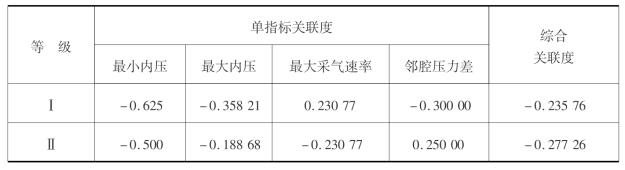
续表

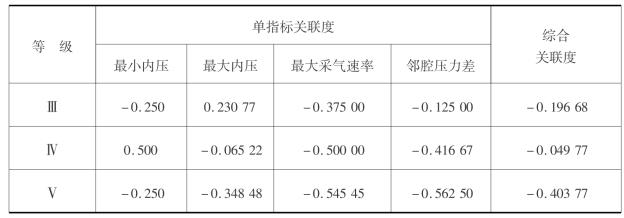
注：最小内压、最大内压、最大采气速率、邻腔压力差的权重分别为0.363 6、0.181 8、0.363 6、0.090 9；级别变量特征值为2.873。

（2）目标层可拓评价

由以上的计算，可以得出3个描述物元（盐岩力学参数，储气库腔体参数，储气库运行参数）的级别变量特征值分别为4.187、3.180、2.873。把描述物元对应于5个等级进行均匀取值，分别对应于（0，1），（1，2），（2，3），（3，4），（4，5）。分别计算单指标关联度和综合关联度。目标物元可拓法评价结果见表6.15。

表6.15　目标层可拓评价结果

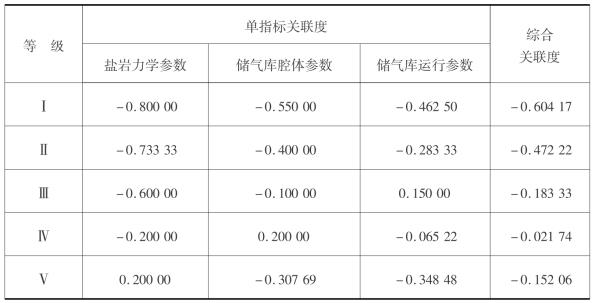
注：盐岩力学参数、储气库腔体参数、储气库运行参数的权重分别为0.333 3、0.333 3、0.333 4。级别变量特征值为3.853。

从表6.15可知，金坛西1储气库稳定性综合评价的级别变量特征值为3.853，运营期储气库处于Ⅳ级，为稳定状态。

6.5　金坛西1储气库稳定性模糊综合评价

模糊综合评价是利用隶属函数作为桥梁将模糊性加以量化，适用于评价具有模糊的非量化因素的对象，在岩体工程稳定性评价中得到了较为广泛的应用。

6.5.1　模糊综合评价及评价过程

对于给定对象的模糊综合评价，设给定2个有限论域

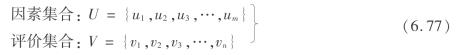
式中 元素Ui（i＝1，2，…，m）——影响评价对象的若干因素；

Vi（i＝1，2，…，n）——若干可能作出的判断结果。

令

式中　A——因素权重集A＝｛a1，a2，a3，…，an｝，表示各评价指标对于评价结果的影响程度；

　R——综合评价矩阵，描述因素集U与评价集V之间的关系；

　B——模糊综合评价集，表示最终评价结果的集合。

在储气库评价体系设计中，将评价对象分为了指标层、描述层和目标层，因此，需要进行多级模糊综合评价。

多级模糊评价就是先把评价的某一事物的多种因素按其属性分为若干类大因素，然后对每一类大因素进行初级的综合评价，最后再对初级评价的结果，进行高一级的综合评价，其过程如下：

①确定因素集U，按其不同属性分成若干互不相交的因素子集U＝｛u1，u2，u3，…，um｝，评价集V＝｛v1，v2，v3，…，vn｝。

②对每个Uk（k＝1，2，…，n）进行初级综合评价。

根据Uk＝｛u1，u2，u3，…，uknk｝中各因素的作用大小，赋予相应的权重Ak，Ak＝｛ak1，ak2，ak3，…，aknk｝且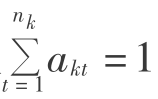；对Uk中的每个因素uknk按照评价集V＝｛v1，v2，v3，…，vn｝的等级评定出uknk对Vj的隶属度rkij（i＝1，2，…，m；j＝1，2，…，n），由此组成单因素评价矩阵Rk。然后可以得出Uk的一级综合评价结果为

③对U进行综合评价，将U中的n个元素U＝｛u1，u2，u3，…，um｝视为U上的n个单因素，按各Uk在U中所起作用的大小确定权重Ak，Ak＝｛ak1，ak2，ak3，…，akn｝；由各Uk的评价结果Bk（k＝1，2，…，n），得出总的评价矩阵为

则得出U的综合评价为

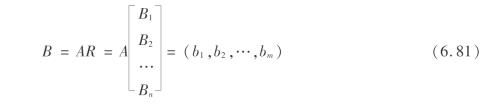
6.5.2　西1储气库模糊综合评价及结果

西1储气库运营期稳定性评价指标取值见表6.11。根据各指标评分模型计算得到各指标分值，将其代入梯形分布隶属函数为

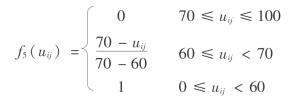
得到各指标对Vj的隶属度及模糊关系矩阵R。进而得到综合评价矩阵B＝WR。最后，求得储气库运营期稳定性的综合得分M＝BV T。评价结果见表6.16。

表6.16　西1储气库模糊综合评价结果

由6.11表可知，金坛西1储气库稳定性综合模糊评价得分为80.10，处于Ⅳ级，为稳定状态，与可拓法评价结果一致。