4.3 自适应技术的理论基础
4.3.1 注水原理
香农从理论上证明,当发送的数据信息速率不大于信道容量时,就有可能以任意小的误码率在给定的信道上进行信息传输。所以在可靠传输要求下,信道容量是数据传输速率的极限。
一个理想传输的高斯信道的信道容量为
![]()
式中,接收信噪比SNR=Pav/Pn,单位为分贝(dB),Pav是信号的平均功率,Pn是信道带宽内的平均噪声功率,B是信道的带宽。信道的容量大小与信道带宽B和接收信噪比SNR有关。
在AWGN信道中,通常不管使用哪种编码和调制方式,数据的传输速率总会低于信道容量。可以认为实际的数据传输速率没有充分利用信道所提供的所有信噪比。此时,实际传输速率 Rb与信噪比SNR之间的关系可以表达为

式(4-2)的含义是采用某种编码方法和调制方式所能达到的实际传输速率 Rb,等同于信噪比SNR损失了一个因子Γ后的信道容量。Γ表示为在一定误码率要求下,使用某种信道纠错编码方式和调制方式,传输速率达到一定时,理论上所需的功率与实际上所需的功率的比值(间隔),称为信噪比差额(SNR Gap)。Γ是一个与目标误码率、调制方式,以及信道纠错编码方式都相关的量。当Γ=1时,表示为系统对功率的利用最为理想。通常情况下,Γ为大于1的常数,表明系统对信噪比的实际利用能力或功率利用率降低。
设计系统数据传输速率时,由于信道状态特性是随机的,因此有必要留出一个信噪比余量(SNR Margin)γm,目的是当信道状态特性变差时,仍然不会影响系统的数据传输速率和性能。当系统将信噪比余量γm考虑其中时,实际传输速率可表示为
![]()
在多载波系统中,H(f)表示信道的传输增益,加性高斯白噪声功率谱密度为 N(f),信号的功率谱密度为 Sx(f)。将传输信道划分成无数个(N→∞)平坦窄带子信道,每个子信道的带宽为Δf→0,而且认为每个子信道的传递函数都是常数。因此信道容量C就可以通过对所有子信道的信道容量进行积分后得到。
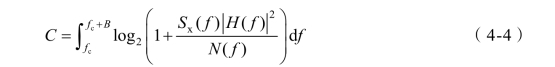
假设信号的总发射功率为 PT,则有

考虑到上式的约束条件,为达到信道容量的最大化,可以利用拉格朗日乘子法将其变换为(https://www.daowen.com)
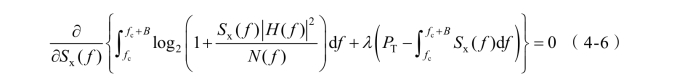
式中,λ为拉格朗日乘数,经过求解得到
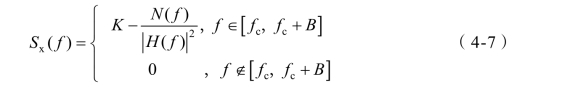
其中

图4.1所示为注水功率分配的示意图,曲线表示不同频率f所对应的信噪比的倒数。这种信道容量最大化的实现方法与将水倒入曲线上方阴影部分的“碗”中(阴影部分的面积表示平均发射功率 PT)类似,从而得到 Sx(f)。这种方法被形象地称为“注水”分配法。
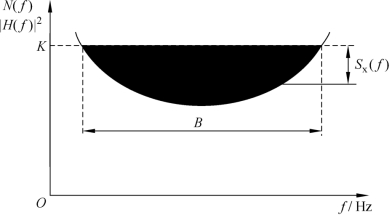
图4.1 注水功率分配示意图
4.3.2 自适应分配原则
按照传输速率,可以将OFDM自适应分配算法划分为两类:变传输速率算法和固定传输速率算法。
1.基于信道容量最优化的原则
该优化原则为变传输速率算法,即在给定的系统误码率和总发射功率的情况下,实现传输速率(即信道容量)最大化,也称之为最大比特率准则,即RA(Rate Adaptive)准则。对应的优化模型可表示为

2.基于发射功率最小化的原则
在给定的系统误码率和传输速率的条件下,根据信道增益对各个子载波上的比特数进行自适应加载,同时对各个子载波上的发送功率进行调整,使总发送功率最小,该优化原则为变功率算法,也称之为功率最小化准则(MA准则)。对应的优化模型可表示为

