4.5 自适应比特功率加载算法
4.5.1 Chow算法
Chow算法的分配原则是根据各个子信道的信道容量来进行比特数的分配[16][17][18]。首先在满足给定目标误比特率的条件下,使系统信道容量达到最优;其次使用迭代过程,逐步对子信道进行比特分配,同时使余量逐步增大,直至所有待分配比特都分配完成。为了确保算法的收敛速度需要设定一个最大的迭代次数。
该算法由三个步骤完成:首先,确定系统的性能达到最优的余量门限γmargin;其次,确定各个子载波上的调制方式;最后,调整各个子载波上的功率。
具体描述如下:
(1)由式(4-18)和式(4-19),计算各个子载波上的信噪比Ssnr(i),∀i∈{1,2,…,N},并且假设所有子载波上的信号能量都进行了归一化,即ε(i)=1,∀i∈{1,2,…,N}。
(2)令迭代次数 Iic=0,γmargin=0(dB),已使用的子载波数Uuc=N,其中N为可用子载波的最大数目。
(3)从 i=1到N计算各个子载波上分配的比特数 b(i)、bˆ(i)、diff(i)、Uuc:

其中round(·)为取整函数,diff(·)为计算理论值加载的比特数与实际加载比特数的差值,γmargin是最优的门限。Γ是信道的信噪比差额,在固定误码率 bBER的情况下,Γ为常数。在MQAM调制方式下,误码率 bBER和信噪比差额Γ的关系可以表示为[19]

(6)Iic=Iic+1。


其中B为OFDM符号带宽,即子载波数乘以符号周期的倒数,Sav为每个子载波上的平均信噪比、Pav为每个子载波上的平均功率,令其归一化为1,Ku为光OFDM携带有用信息的子载波数。
4.5.2 Hughes-Hartogs算法
算法的主要思想是:首先,将所有子载波上的比特数设定为0;其次,再将所有待分配比特依次分配给各个相应的子载波。在每次分配比特过程中,先找到增加2比特时,只需要增加最少发送功率就可以维持目标误比特率的子载波。其后将该子载波上的比特数加2,重复该过程直至所有待分配比特数分配完成。最后,计算各个子载波上所需的发射功率。
该算法分为两步进行:
1.比特分配
(1)将所有子载波的比特数和功率初始化均设为0,即
![]()
(2)计算每个子载波增加2比特数据信息时所需增加的功率,即差额功率(https://www.daowen.com)
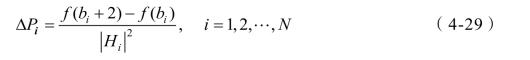
(3)根据公式(4-29),求{ΔPi}中的最小值,及对应的子载波编号id,
![]()
其中min(·)为求最小值的函数。
(4)给编号为id的子载波分配2比特的信息,即

(5)置ΔPindex_min=∞,转至(3)。
2.功率分配
如Chow算法。
4.5.3 Fischer算法
该算法的优化准则是根据差错概率最小化的原则,分为两步进行。
1.初始化
(1)首先,必须已知各个子载波上噪声方差Ni(其中 i=1,2,…,N),Ni可认为是信道增益平方的倒数。其次,设定目标比特速率(即分配的比特数 Rb)。N′表示已使用的子载波数,设N′的初始值N′=N。令激活的子信道集合为I,设I的初始值I={1,2,…,N}。
(2)计算所有子信道的噪声功率值Li=log2(Ni),(i=1,2,…,N),然后将 Li的值存储起来,这样就不需要重复地进行对数运算。
(3)计算I中各个子信道可分配的比特数:

如果 b(i)≤0,i∈I,那么N′=N′-1,把第i个子信道从I中删掉然后转至步骤(2),继续计算,直到 b(i)>0,i∈I。

2.功率分配
如Chow算法。
