9.1.2 数据流分析
数据流分析将给出关于程序中是如何使用变量的保守信息。这些信息一般是通过对控制流图的计算得到的。而对于过程间数据流分析,这些信息则是同时计算控制流图和函数调用关系图获得的。数据流分析能够回答的问题如下。
(1)当程序执行到某个位置p之后,变量x的值应该是什么?
(2)变量x在函数的哪些地方被使用?或者在位置p上,变量x是否已经被赋值了?
(3)函数中,变量x在位置p上是一个常量吗?如果是的话,这个常量的值应该是什么?
例如,RECG反编译算法中,就使用了数据流分析的方法。它把汇编语言中的“测试指令—条件转移指令”转换成“if…goto…”这种较为高级的形式,如图9.11所示。
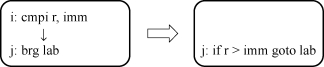
图9.11 测试一条件指令转换为if…goto…
要做到这一点,我们必须确定“测试指令”到底会设置哪些标志位。而这就是数据流分析中常见的“到达定值”问题。
图9.12是模n幂运算函数的控制流图。其中标出了程序中每个变量的使用定值链(或简称ud链,ud-chain)。
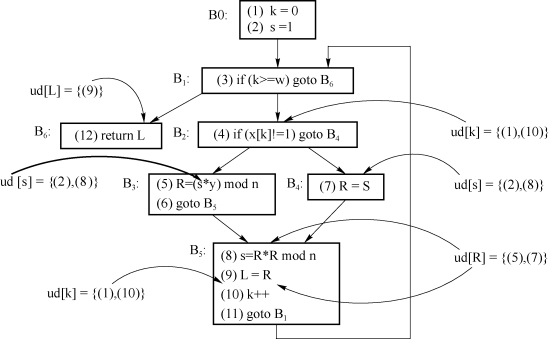
图9.12 模n幂运算函数的控制流图
在每个变量所有被使用的地方,ud链都会给出该位置上这个变量的值是由哪条/哪几条语句定值的。以语句(5)中的变量s为例:在第一次执行这个语句时,变量s的值是由语句(2)定值的。可是当循环进行了几轮之后,s的值就由语句(8)确定了。所以在语句(5)中s的ud链就是集合{(2),(8)}。我们说ud链表示的信息是保守的,因为它会把程序执行中所有可能的情形全部考虑进去,哪怕在运行时可能不会发生的那些情形也不例外。例如,由于无法确认在B2处控制流会转向哪边(因为我们不会去运行这个程序),所以我们不得不假设这两种情况都可能发生,故而在语句(8)中,变量R的ud链只能是{(5),(7)}。
要计算ud链,我们首先要解决一个名为“到达定值”的数据流分析问题。数据流分析是一系列算法的统称,这类算法一般都是迭代算法,它们获取的信息则表现为一些关于值的集合。对于“到达定值”问题,实际上就是要求解in[B],out[B],gen[B]和kill[B](其中B指控制流图中任意一个基本块)组成的方程组,如图9.13所示。方程组的解就是我们所关心的问题——各个变量都是由哪些语句定值的。
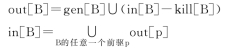
图9.13 到达定值方程组
对于各个基本块而言,gen和kill只要计算一次就够了。gen[B]中包含所有基本块B内对变量进行定值语句,且该定值能到达B的结尾处(即该变量在这条语句之后不会再被后续的其他语句赋值)的语句。而kill[B]中则包含了控制流图中其他基本块中一些对变量进行定值的语句,这些语句必须满足定值能够到达B的开头处,且B中含有对有关变量的赋值语句,使该定值不能达到B的结尾处(也就是说这个定值被B中的赋值语句kill(杀死)了)。gen和kill计算示意图如图9.14所示。
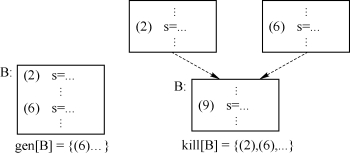
图9.14 gen和kill计算示意图
一般而言,数据流问题总是可以被分为两部分:单独考虑各个基本块的局部分析(如到达定值问题中的gen和kill集)和综合考虑各个局部分析成果的全局分析。在到达定值问题中,计算in[B]和out[B]就属于全局分析。in[B]就是所有能够到达基本块B开头处的定值语句的集合(即所有对变量进行赋值,且在运行时该定值可能到达B开头处的语句的标号)。in和out计算示意图如图9.15所示。
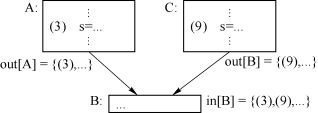
图9.15 in和out计算示意图(a)
同样,out[B]就是所有能够达到B结尾处的定值语句的集合,即所有对变量进行赋值,且在运行时该定值可能到达B结尾处的语句的标号,如图9.16所示。
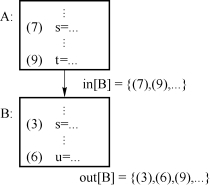
图9.16 in和out计算示意图(b)
对于各个基本块来说,in和out是需要反复迭代计算,直到到达一个不动点(fix-point)为止。下面给出计算控制流图到达定值问题的算法。

对于本章开头给出的幂运算程序,在进行了三轮递归运算之后,到达了不动点,结果如图9.17所示。根据集合in,我们就能轻松写出ud链。
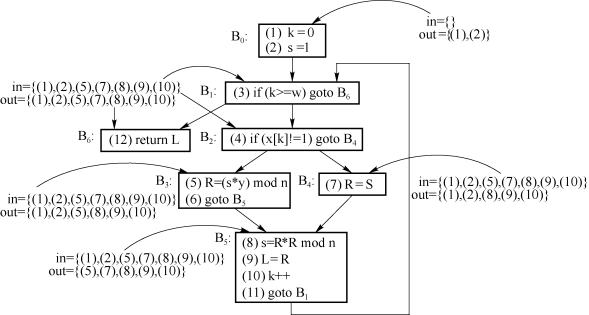
图9.17 ud链
定值使用链(du链)基本上与ud链是类似的,只不过它修改成变量的定值语句上标出这些定值会在哪里被使用而已,如图9.18所示。
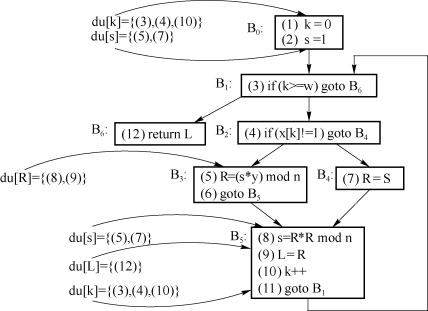
图9.18 du链
除了信息流是后向的之外,计算du链的数据流分析算法实际上也是到达定值算法。一般而言,根据关心的性质是必须在所有路径上都成立,还是只在某一条路径上成立就可以,可以将数据流分析算法分为部分路径(any path)和全部路径(all paths)两种。根据数据流分析时迭代是顺着控制流的方向,还是逆着控制流的方向进行的,又可以把数据流分析算法分为前向的(forward flow)和后向的(backward flow)两种。于是就能得出4种基本的数据流框架,对应表9.1给出的这4个方程组。掌握了它们,你就能应付各种数据流分析问题了。
表9.1 到达一定值算法

