9.1.4 别名分析
如果两个指针指向了同一个内存地址,那我们就说这两个指针互为别名。别名分析就是要确定当程序运行到某个位置p上时,两个变量a和b是否可能或必然指向同一个内存地址。为了更形象地说明这一问题,我们来看下面这段代码。
那些不够专业的编译器及程序员会以为上面的这个测试是永远为假的。难道不是吗?循环一共进行10次,每次a的值都会加一,所以当离开上面这个循环时,a的值就是10。所以语句S是一个可以删除的死代码。但当真如此吗?我们来看这个代码,它给变量a创建了一个别名*x,它们都指向同一个内存地址!所以深灰色标出的这个代码也会改变a的值,循环实际上只会进行一次,上面的测试是永远为真的,语句S肯定会被执行!如果一个优化编译器“看不懂”这种小花招,它就会产生错误的代码。不只是编译器,所有代码转换工具(包括本书中介绍的代码保护工具)都必须能够处理这类问题。
1.别名是如何产生的
在很多种情况下都会产生别名,它会给人工分析和自动代码转换工具带来不小的麻烦。例如下面这段代码。
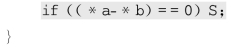
当你看到*a-*b这行代码时一定想:10-5=5,添加了灰色底纹的测试永远不会为真,语句S也绝不会被执行!你大笔一挥,把这个if语句给“优化”掉了。可是你有没有想过,自此代码里就多了一个漏洞——若用formal_formal(&x,&x)调用这个函数可怎么办呢?这时*a和*b都指向同一个内存空间,*a-*b结果就变成了0!
上述这类别名问题是由函数的两个参数指向了同一个内存地址而引发的,但是函数的某个参数再加上一个全局变量也会引发类似的问题,例如:
上面这段代码中,如果用formal_global(&x)调用formal_global()函数,就会引发*a和x之间的别名问题,使if语句的测试结果永远为假。
别名问题还会由函数的副作用引发。在下面这段代码中,调用完函数foo()之后,x和y就指向了同一个内存地址(变量t),因此语句S就总是会被执行。
最后,别名问题还会因数组中的元素而引发,如下面的例子。
粗心的读者一定认为a[i]-a[j]一定是等于5。可惜你错了。i和j现在都是2,所以a[i]和a[j]指向的是数组的同一个元素,它们互为别名,因此a[i]-a[j]的结果一定是0。
2.别名分析的分类
我们把别名分析分为两大类:可能别名(may-alias)和必然别名(must-alias)。令a和b分别为程序中对内存地址的两个引用。当程序运行至某个点p时,如果程序沿着某条路径执行,a和b会指向同一个内存地址,则称a和b互为可能别名,记为
∈may-alias(p)。而如果不论程序沿哪条路径执行,a和b总是指向同一个内存地址,则称a和b互为必然别名,记为
∈must-alias(p),如图9.20所示。
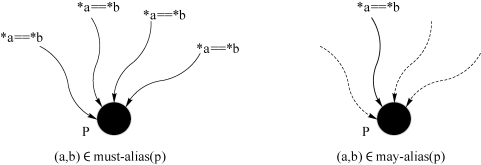
图9.20 别名分析示意图
在下面这段代码中,位置p1上有一个必然别名must-alias(p1)=
,而p2上则是一个可能别名may-alias(p2)=
。
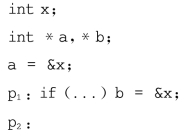
如果程序里有很多指针,那么进行别名分析所需的计算量就会很大,这时你将不得不根据实际情况选择不同的算法,在性能和结果的精确性之间作出权衡取舍。可供选择的算法分为流不敏感的和流敏感两种。流不敏感的算法对程序或函数进行别名分析时会忽略控制流,而流敏感的算法则不会。一般而言,流不敏感的算法执行起来更快,但是结果的精确性略差,而流敏感的算法相对会比较慢一些,但结果更精确。
我们用下面这个例子来说明流敏感的算法与流不敏感的算法之间的区别,例子中
表示p和q互为可能别名。
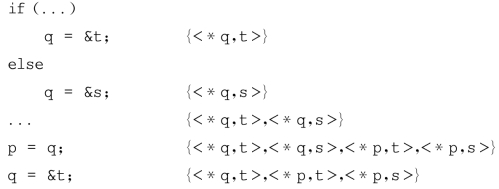
上例中,我们已经在程序里的每条语句边上都已标上了相应的别名集,这些别名集是由流敏感的算法产生的,而流不敏感的算法所产生的别名集则模糊得多,它在每条语句边标上的别名集都是
。
此外,在别名分析时是否把被调函数考虑在内也会给性能和结果的精确性带来影响。过程内别名分析(又称“上下文不敏感的”别名分析)只是单独对各个函数进行别名分析,当遇到函数调用时,它只是最保守地估计被调函数对主调函数的影响。而过程间别名分析(又称“上下文敏感的”别名分析)则会具体考虑各个被调函数对主调函数可能产生的影响。
一般而言,我们认为别名分析算法(以及所有静态分析)都应该是保守的。也就是说,也许别名分析算法会报告两个指针p和q可能指向同一个内存地址,尽管这种情况实际上并不会发生。或者你也可以这样认为,除非你能证明在点r,p绝对不可能与q指向同一个内存地址,否则,就必须写上
∈may-alias(r)。但在某些应用(如在程序中寻找漏洞)中,如此谨小慎微却是没有必要的。如果我们能“胆子更大一点,步子更快一点”,分析的效率往往就会显著提高。
实践中我们所使用的许多算法都是流敏感的和上下文敏感的。Hind和Pioli在报告中指出:(在代码优化编译器所使用的算法中)流敏感的算法的结果“最为精确”。说到底,我们认为,当别名分析被用于攻击本书中介绍的软件保护技术时,攻击者对结果精确性的要求一定会比编译器的要求更高。
本书中介绍的另一类算法特别钟情于形制分析(shape analysis),又称对分析(heap analysis)。在这类分析中,我们所要确定的是,存放在堆中(地址被记录在某个指针中)的某个东西究竟是个什么数据结构:数?有向无环图(DAG)?还是一个循环图?和其他的别名分析算法一样,在形制分析时也必须在性能和结果的精确性之间作出折中。Ghiya提出的算法也应付不了这种更新时会破坏数据结构的代码,它分析顺序添加链表元素的代码时表现良好,但要是把同样操作反过来进行,它就无能为力了。其他还有一类算法对递归的深度有一定的要求,如不能超过某个常数k。而Hendren的算法则不能应付带循环的数据结构。
Ramalingam已经证明:对于支持动态内存空间分配、循环和if语句的语言来说,结果更精确的流敏感的别名分析是一个不可判定的问题。即使是流不敏感的算法,要进行较为精确的可能别名分析也是一个困难的问题。通常,结果不精确的别名分析算法与低阶多项式呈线性关系。Hind和Poli的报告中指出:要达到同等的精确度,流敏感的算法要比流不敏感的算法慢到原来的1/4,还要比流不敏感的算法多用6倍的内存空间。
3.别名分析的算法
Michael Hind曾撰文指出,自1980年至2001年间,关于别名分析方面,共发表了75篇论文及9篇博士论文。虽然文章数量如此众多,但究其根本都仅是根据不同需要在性能和精确性之间作出不同选择的产物而已。所以只需介绍其中两个就足以使你大致了解这些算法的全貌了。我们下面要介绍的一个是基于类型的流不敏感算法,另一个是基于数据流分析的流敏感算法。
在Java和Modula-3这类强类型语言中,我们可以使用基于类型的别名分析算法。这个算法的思路很简单,如果p和q是指向不同类型对象的指针,那它们就绝对不可能互为别名!在C语言这种不安全的语言中可没有这回事!因为这类语言中,程序员可以使用强制类型转换随心所欲地混用各种类型的指针。在下面这段Modula-3代码中,p和r可能互为别名,但是p和q则绝不可能互为别名。
上例中使用的是一个流不敏感的算法,所以你无从知晓p和r实际上指向的是不同的对象。
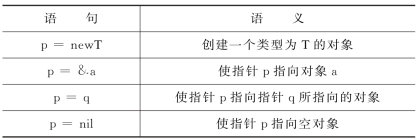
下面我们再来看一个流敏感的可能别名分析算法。这个例子源自大名鼎鼎的《龙书》,假设某种语言使用的是常用的控制结构,并且支持下列指针操作(见表9.3),这个算法使用了前向数据流分析算法,分析的结果用
形式的别名对的集合来表示,其中p和q表示访问路径,它可以是:
表9.3 某编程语言的指针操作
(1)类似
的左值表达式;
(2)程序中的位置,如S1、S2等。
每当程序中使用new操作符创建一个新对象时,就必须以某种形式给新创建的对象命名。可理论上程序中可以创建无穷多个新对象,故而我们找不出一个完美的命名方法。简便起见,我们直接使用new语句在程序中的位置来表示新创建的对象。这当然是有潜在的风险的,如果在同一行代码中有两个new操作符,那么这两个对象的名字就会一模一样!可怎么办呢?这就像在别名分析时要折中一样,选用这类命名方案时也得讲点中庸之道。
如果分析完毕之后,在数据流方程中有
∈in[b],那就说明,在基本块b的开头处p和q是指向同一个内存地址的。
transb(S)是转换函数,其中S就是在基本块b开头处的别名集。而transb(S)则是在基本块b结尾处的别名集。这个转换函数定义如表9.4所示(有关语句的语义前文已述)。
表9.4 转换函数定义
表9.4中,(S-
|any a})表示不论p之前指向什么,在执行了该语句之后,它已经变为无效了。在规则1中,在执行了语句p=new T之后,p已经指向了新对象d了。语句p=new T前的d:表示该语句在程序中的位置,所以我们也用它来命名新创建的对象。在规则2中,在执行了语句p=&c之后,p与c互为别名。规则3中,在执行了语句p=q之后,p已经指向q所指向的对象了。
例如,对于下面这个程序:
经过第一轮迭代,我们获得的in和out集如图9.21所示。
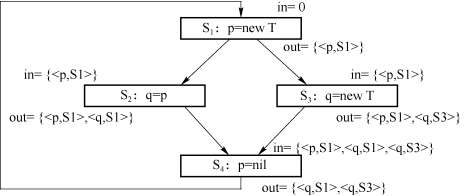
图9.21 in和out控制流图(a)
再经过一轮迭代之后,我们到达了不动点——得到了最终的结果,如图9.22所示。
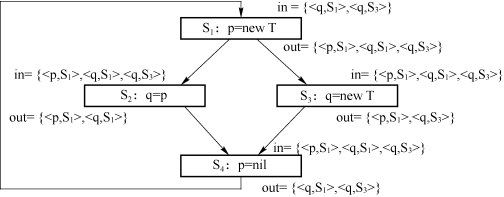
图9.22 in和out控制流图(b)
当控制流流至语句S4,但尚未执行S4时,指针q有可能指向语句S1中创建的对象(如果控制流往左走的话),也有可能指向语句S3中创建的对象(如果控制流往右走的话)。