附录1
归谬法和2的平方根

毕达哥拉斯学派对“2的平方根为无理数”的原始论证基于“归谬法”：假设某命题为真，如果以此推导出了矛盾或荒谬的结论，则该命题必然错误。我们可以举个现代点的例子。20世纪伟大的物理学家尼尔斯·玻尔有句格言：“每个伟大的思想，其对立面是另一个伟大的思想。”如果这句名言是对的，那结果至少有点儿危险。想一想老生常谈的“应当推己及人”“不该说谎”或者“不该杀人”就明白了。我们还可以假定玻尔这句格言本身也是个伟大的思想，这样一来，它的反面“每个伟大的思想，其对立面不是伟大的思想”也一定是正确的。这时候，谬误就出现了。如果它的对立面是错的，那我们就无须奉玻尔的名言为圭臬，因为它证明了自己不是。

毕达哥拉斯学派在通过归谬法论证2的平方根是无理数时，采用了专业的几何学方法，而我们可以用更现代，也更简单的代数方式。论证的过程、思考的方式，至少和结论一样有趣：

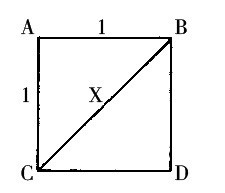
想象一个边长为1的正方形（这个1是厘米、英寸，或者光年都无所谓）。对角线BC将这个正方形切分成了两个直角三角形。按照毕达哥拉斯定理，这样的直角三角形中1²+1²=X²，所以X²=2，X=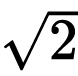。即2的平方根。我们假定X=p/q，且是一个有理数，所以p和q都是整数。对它们的大小，我们不做任何要求，但不得有公约数。举个例子，14/10里p=14，q=10，但它们都可以除以2，得p=7，q=5，即7/5。开始前，我们需要除去所有公约数。p和q的取值有无穷多的选择。从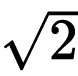=p/q开始，将等号两边都平方，得到2=p²/q²，或者我们把两边都乘以q²，得

p²=2q²（方程1）

p²是某个数乘以2，因此p²是偶数。但任何奇数的平方根都是奇数（1²=1，3²=9，5²=25，7²=49，等等），所以p本身也必然是偶数。我们可以写p=2s，s为另一个整数。将p代入方程1，得

p²=（2s）²=4s²=2q²

等式两边都除以2，得

q²=2s²

因此q²是偶数。根据我们刚才对p的讨论，可得q也是偶数。但如果p和q都是偶数，就都能被2整除，没有得到完全约分，与我们的假设相矛盾。这就是归谬法。但问题出在命题的哪个部分？从论述中，我们得不出公约数错误的结论，也即14/10可行但7/5不行，所以问题只能出在最初的假设上；p和q不可能都是整数，2的平方根只能是无理数。实际上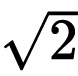， =1.4142135……

多么令人震惊，又出人意料的结论啊！这个证明，又是多么优雅！可惜毕达哥拉斯学派认为有必要保守这伟大的发现。