9　麦克斯韦妖

在这几个月非凡的冒险历程中，教授引领汤普金斯先生越来越深入地理解了物理学的奥秘，汤普金斯先生也越来越深地爱上了莫德，直到最后，他终于羞怯地向她求了婚。莫德立即答应了他的请求，他们很快就结成了一对儿。作为一位新晋的岳父，教授认为自己有责任向女婿普及物理学知识，向他介绍这门学科的最新进展。

一个星期天的下午，在那间温馨的小公寓里，汤普金斯先生和太太舒舒服服地坐在扶手椅里，太太随手翻着最新一期的《时尚》，汤普金斯先生正在读《时尚先生》里的一篇文章。

“噢，”汤普金斯先生突然开口说道，“原来真有稳赢不输的赌术！”

“西里尔，你觉得真有这样的好事儿吗？”莫德从时尚杂志中抬起头来，有些责备地问道，“父亲总说，世上根本就没有稳赢不输的赌博策略。”

“可是你看，莫德，”汤普金斯先生翻开他刚才读了半个小时的那篇文章，把杂志递给太太，“我不知道其他策略到底有没有用，但这套赌术的基础是最简单纯粹的数学。我完全看不出来它哪儿有问题。你只需要把1，2，3这三个数写在纸上，然后遵循文中介绍的一套简单规则就行。”

“那我们试试吧。”莫德开始感兴趣了，“规则是什么样的？”

“要想理解这套规则，最好的办法就是看看文章里的例子。根据文中的描述，他们玩的是轮盘赌，你可以押红或者押黑，就和硬币猜正反一样。我先写个

1，2，3

按照规则，我押的赌注必须是头尾两个数字之和。所以第一把，我应该押上1加3个筹码，呃，就押红色吧。如果我赢了，我就把1和3这两个数字划掉，下一轮的筹码数量应该是仅存的那个数字，也就是2个；要是我输了，我就把自己输掉的筹码数量加在数列后面，按照同样的规则确定下一次的赌注数目。呃，假设第一轮的球停在了黑色区域，荷官收走了我的4个筹码，那么现在我的数列就变成了

1，2，3，4

因此第二把的赌注应该是1加4，也就是5个筹码。假设第二次我又输了，那么按照文章中介绍的方法，我必须坚持下去，把数字5加到数列末尾，第三轮押上6个筹码。”

“但你这次肯定会赢！”莫德激动地大喊，“你不可能一直输下去。”

“这可不一定。”汤普金斯先生说道，“小时候我和朋友一起扔硬币玩，不管你信不信，我连续见过十次正面。但现在我们按照文章中的假设，这次就让我赢吧。那我一共将收回12个筹码，但和我投入的成本相比，我还输着3个筹码呢。按照这套规则，我必须把数字1和5划掉，那么我的数列变成了

1，2，3，4，5

下一轮的赌注应该是2加4，还是6个筹码。”

“文章里说，这次你又输了。”莫德叹了口气，趴在丈夫肩头读着杂志上的文章，“这意味着你应该把数字6加到数列后面，下一轮押上8个筹码，没错吧？”“没错，就是这样。但我又输了一次，现在我的数列变成了

1，2，3，4，5，6，8

这次我得押10个筹码了。然后我赢了。划掉数字2和8，下一轮的赌注是3加6，也就是9个筹码。于是我又输了。”

“真是个糟糕的例子，”莫德嘟着嘴抱怨，“目前为止，你一共输了三次，但只赢了一次。这不公平！”

“没关系，没关系。”汤普金斯先生像魔术师般胸有成竹地安抚妻子，“玩到最后我总会赢回来的。刚才这把我输掉了9个筹码，所以我把这个数字加到数列最后，让它变成

1，2，3，4，5，6，8，9

下一轮应该押12个筹码。这一次我赢了，所以我划掉数字3和9，押上4加6个筹码。我又赢了一次，现在所有数字都被划掉了，循环结束。算一下总账，我一共赢了6个筹码，虽然事实上我只赢了4次，但却输了5次！”

“你真的赢了6个筹码？”莫德狐疑地问道。

“我很确定。你看，按照这套规则，每完成一次循环，你必然会赢6个筹码。你可以通过简单的算术来证明这个结果，所以我才会说，这套规则基于数学，不可能出错。要是你不相信，你可以拿张纸自己验算一下。”

“好吧。我就相信你一回。”莫德若有所思地说，“可是，当然，6个筹码不算多。”

“要是你能保证每次循环都赢6个筹码，那也不少了。你可以不断重复这个过程，每次都从1，2，3，开始，这样一来，你想赢多少钱就能赢多少。是不是棒极了？”

“真是太好了！”莫德赞叹道，“那你可以辞掉银行的工作，我们也能搬到更好的房子里住，今天我还在商店橱窗里看到了一件特别漂亮的貂皮大衣，只卖……”

“我们当然会买下那件大衣，不过首先，我们得赶快动身去蒙特卡罗。肯定有很多人读了这篇文章，要是去得晚了，别人早就把赌场赢得破产了，我们只能干瞪眼！”

“我这就打电话给航空公司，”莫德提议说，“问问下一班飞机什么时候起飞。”

“你们这是急着去哪儿呀？”客厅里响起一个熟悉的声音，莫德的父亲走进房间，惊讶地望着激动的小两口。

“我们要搭第一班飞机去蒙特卡罗，然后带着大把的钞票回来。”汤普金斯先生起身迎接教授。

“喔，我明白了。”教授露出微笑，舒舒服服地坐进了壁炉旁边的一张老式扶手椅里，“你有一套新赌术？”

“但这套规则真的稳赢，父亲！”莫德抗议道，她的手还没有离开电话。

“是啊，”汤普金斯先生一边附和，一边把手里的杂志递给教授，“简直万无一失。”

“是吗？”教授笑道，“让我看看。”他读了一会儿文章，然后继续说道，“这套规则的特点在于，它要求你每次输钱之后都提高赌注，与此同时，每次赢钱之后都降低赌注。这样一来，如果你比较规律地交替输赢，那么你手里的筹码时多时少，但总体而言，每次增加的幅度都大于上一次减少的幅度。在这种情况下，你当然可以在短时间内成为百万富翁。但你肯定明白，现实中根本不存在‘输赢有规律’这回事。事实上，规律地交替输赢，这种事情发生的概率和你一直赢下去一样小。所以我们必须考虑连赢或者连输几次的情况。如果你踏进了赌徒们常说的幸运之河，那么按照规则，你每次赢钱之后都必须降低赌注，或者至少不能增加赌注，所以你总共赢的钱不会太多。从另一方面来说，由于每次输钱之后都必须增加赌注，那么连续输钱势必带来更大的损失，这可能让你彻底出局。现在你应该明白了，代表你手中筹码数量的曲线可能平缓地上升几次，然后被陡然的下降打破。游戏刚开始的时候，你可能会画出一条缓慢上升的长曲线，看着自己手里的钱缓慢但坚定地增加，享受片刻愉快的感觉。但是，为了博取更高的收益，你会一直玩下去；总有那么一次，曲线会毫无征兆地出现断崖式的下跌，迫使你押上兜里的最后一分钱，然后输得一干二净。我们可以利用通用的办法来证明，无论是按照这套规则还是其他规则，筹码曲线翻倍的概率和归零的概率完全相等。换句话说，最后你赢钱的概率其实就等于直接把所有钱押在红区或黑区上，然后一把翻倍或者输光。所谓的赌术能做的只是尽量延长这个过程，让你获得更多乐趣。但是，如果你只想找点乐子，那完全不必搞得这么复杂。你看，轮盘上有36个数字，你可以同时押35个数字，只留一个不押。这样一来，你赢钱的概率高达35/36，荷官会赔你36个筹码，比你的本金多1个。但是，大约每转上36次，轮盘上的小球就会有一次掉进你没赌的那个格子里，你会一下子输掉35个筹码。按照这套策略，只要你玩的时间足够长，那么你的筹码曲线看起来和杂志上介绍的策略一模一样。

“当然，刚才我假设的前提条件是赌场不抽水。但事实上，我见过的所有轮盘都有0这个数字，有时候还有两个0，这增加了玩家输钱的风险。这样一来，无论玩家采用什么策略，他的钱都会慢慢从自己兜里漏到赌场老板兜里。”

“你是想告诉我，”汤普金斯先生沮丧地说，“世上根本没有稳赢的赌术，无论怎么努力，你输钱的风险总是比赢钱的概率高一点点？”

“我正是这个意思，”教授说，“还有，我刚才说的不光适用于这些无伤大雅的概率游戏，也同样可以用来描述各种乍看之下似乎跟概率完全无关的物理现象。举个例子，要是你真的想出了一套能够推翻概率定律的规则，那么它的威力绝不仅仅是赢几个钱而已。比如说，你可以造出不需要汽油的汽车，不需要煤的工厂，还有其他很多了不起的东西。”

“我似乎在哪儿读到过这种假想的机器——永动机，应该是叫这个名字吧。”汤普金斯先生说，“要是我没记错的话，人们认为我们不可能造出不需要燃料的机器，因为能量不可能凭空产生。但是，这种机器和赌博一点关系都没有啊。”

“你说得对极了，我的孩子。”女婿对物理学至少有那么一点了解，教授深感欣慰，“这种永动机被称为‘第一类永动机’，它之所以不可能存在，是因为它违反了能量守恒定律。但我脑子里想的那些不要燃料的机器和这种很不一样，它们通常被称为‘第二类永动机’，这类机器的设计原则不是无中生有地创造能量，而是从周围的大地、海洋或空气中汲取能量。比如说，你可以想象这样一艘蒸汽轮船，它用来烧锅炉的原料不是燃煤，而是从周围海水中汲取的热量。事实上，如果我们能迫使热量从比较冷的地方流向比较热的地方，而不是相反，那我们就能从冰冷的海水中汲取热量，然后将失去热量的海水冻成的冰块扔回海里。一加仑冷水冻结成冰，这个过程释放的热量足以将另一加仑的冷水加热到接近沸点。如果从海水中抽水的速度能达到每分钟几加仑，那你可以轻松获得足够的热量来推动一台不算小的引擎。从实用的角度来讲，这样的第二类永动机工作起来和凭空产生能量的第一类永动机一样棒。有了这样的引擎，世界上的所有人都能活得像稳赢不输的赌徒一样舒服。不幸的是，第二类永动机也不可能实现，因为它违反了概率定律。”

“我承认，从海水中汲取热量推动蒸汽船的锅炉，这真是个疯狂的想法，”汤普金斯先生说，“但是，我实在不明白这事儿和概率定律有什么关系。当然，你应该不是说，这些永动机的移动部件是由骰子和轮盘构成的。或者……你真是这个意思？”

“当然不是了！”教授大笑起来，“至少我相信，就连最疯狂的永动机发明家也没打过这种主意。重点在于，热过程本身的特性和投骰游戏十分相似，想让热量从冷的地方流向热的地方，这就像盼着钞票从赌场柜台飞进你兜里一样。”

“你是说，赌场柜台是冷的，我的衣兜是热的？”汤普金斯先生彻底糊涂了。

“从某种角度来说，的确如此。”教授回答，“如果你听了我上周的讲座，那你应该知道，热的本质是组成物质的无数粒子（人们称之为原子和分子）的高速无规律运动。这种分子级的运动越激烈，物体摸起来就越热。由于这样的运动是无规律的，所以它遵从概率定理，很容易证明，大量粒子组成的系统最可能的状态就是能量各不相同的所有粒子基本均匀地分布。如果物体某个部位受热，也就是说，该区域的分子运动加快了，那么你可以想象，这些额外的能量很快就将通过大量的随机碰撞均匀地分散到所有粒子身上。但是，由于这些碰撞完全随机，所以也存在这样的可能性：一组特定粒子偶然获得了大部分额外能量，相应地，周围其他粒子获得的能量就少了很多。热量自发聚集于物体某个部位，这相当于热能逆温度梯度流动；从理论上说，我们无法彻底排除这样的可能性，不过，只要算一算你就会发现，这种事情发生的概率非常非常小，足以让我们给它贴上一个‘实际上不可能’的标签。”

“噢，现在我明白啦。”汤普金斯先生恍然大悟，“你的意思是说，第二类永动机可能在短时间内起效，但这种事情发生的概率小得就像你的骰子连续掷出100个7一样。”

“实际概率比这还要小得多。”教授纠正道，“事实上，稳赢不输，这种事情发生的概率低到了你很难找到合适的词语来形容的地步。比如说，我可以计算这间屋子里的所有空气全都自发聚集到桌子下面，让其他地方都变成真空的概率。你一次掷出的骰子数量等于房间里空气分子的数量，所以我必须先弄清这个数字。我记得，大气压下1立方厘米的空气包含的分子数量，这个数字差不多有20位数，所以整个房间里的空气分子数量应该有27位数。桌子下面的空间大约相当于整个房间容积的百分之一，那么任意分子跑到桌子下面——而不是其他任何地方——的概率应该也是百分之一。所以，要计算所有空气分子同时聚集在桌子下面的概率，我必须用百分之一不断地乘以百分之一，连乘的次数等于所有空气分子的数量，最终得到的结果在小数点后面有54个零。”

“呼……！”汤普金斯先生吐出一口长气，“我可不会把赌注押在这么小的概率上！但你刚才说的是不是意味着房间里的空气分子必然均匀分布？”

“没错。”教授回答，“你可以认为我们绝不会因为所有空气都跑到桌子下面而窒息，出于同样的原因，你那个高杯里的水也不会突然自己沸腾。但是，如果我们观察的对象是一些尺度特别小的区域，它包含的骰子——分子——数量很少，那么这些分子分布不均匀的可能性就大大提高了。比如说，就在这个房间里，总会有某些地方的空气分子比其他地方更密集一点，从而造成一种暂时性的不均匀，我们称之为密度的统计波动。阳光穿过地球大气的时候，这种不均匀性会导致蓝光发生散射，这赋予了天空我们熟悉的颜色。要是密度的统计波动不存在，天空就会变成一片漆黑，星星哪怕在大白天也清晰可见。液体在接近沸点时会呈现出轻微的乳白色，这同样可以用分子不规律运动产生的密度波动来解释。但是，在比较大的尺度上，这样的波动出现的概率极低，也许你等上几十亿年也未必能看到一次。”

“但这种小概率的事情也完全有可能现在就发生在我们的眼皮子底下，”汤普金斯先生坚持说，“难道不是吗？”

“是的，当然存在这样的可能性，一碗汤里的半数分子突然同时获得了同一个方向的热速度，于是这碗汤自发地泼到了桌布上——我们没有理由认为这样的事情绝对不会发生。”

“这样的事情昨天刚刚发生过一次。”读完杂志的莫德饶有兴味地插话道，“汤洒了出来，但女仆说她根本没碰过那张桌子。”教授轻笑起来。“就这件事而言，”他说，“我觉得惹祸的更可能是女仆，而不是麦克斯韦妖。”

“麦克斯韦妖？”汤普金斯先生惊讶地重复，“我还以为科学家绝不会相信神鬼妖怪之类的事情。”

“呃，我们也没把它当真。”教授说，“麦克斯韦妖的概念出自著名物理学家克拉克·麦克斯韦（Clerk Maxwell）。这只统计学小妖精其实只是一种修辞，麦克斯韦利用这个概念形象地阐述了热现象。麦克斯韦妖是个动作敏捷的小家伙，它能按照你设想的任何方式改变每一个分子的运动方向。如果真的存在一只这样的妖精，热量就能逆温度而流动，热力学的基本定律——熵增定律——也将变得一文不值。”

“熵？”汤普金斯先生重复道，“我听说过这个词儿。我的同事举行过一场派对，喝了几杯以后，他请来的几位化学系学生就开始唱了——

‘升升降降，

降降升升，

谁会在乎

熵干了什么？’

他们唱的是《噢，亲爱的奥古斯汀》的调子。话说回来，熵到底是什么？”

“这个解释起来不难。‘熵’只是一个术语，它描述的是任何给定物体或物体组成的系统内分子运动的无序度。分子之间大量的无规律碰撞总是倾向于导致熵增，因为绝对的无序是任何统计集合最可能的状态。但是，要是麦克斯韦妖真的存在，他很快就会让分子运动产生某种秩序，就像牧羊犬驱赶羊群一样，这样一来，熵就会下降。我还可以告诉你，根据路德维希·玻尔兹曼提出的所谓H定理……”

教授显然已经忘了，现在他的听众不是大学生，而是对物理学几乎一无所知的门外汉；他滔滔不绝地说着，稀奇古怪的术语一个接一个地往外蹦，什么“广义参数”，什么“准遍历系统”，他觉得自己把热力学基本定律及其与吉布斯统计力学形式的关系都讲得清清楚楚。汤普金斯先生早已习惯了岳父的高谈阔论，所以他从容地呷着威士忌和苏打水，试图表现得心领神会。但对莫德来说，这些统计物理学的精华内容显然过于艰深，她蜷缩在椅子里，努力和睡魔做斗争。为了赶走睡意，她决定去厨房看看晚餐准备得怎么样了。

“夫人有什么需要吗？”她刚走进餐厅，就有一位衣着整洁的高个子管家迎上前来，鞠躬问道。

“没事，你继续干你的活吧。”她一边回答，一边暗自琢磨这人是从哪儿冒出来的。考虑到他们从来没请过管家，也绝对雇不起，这事儿就显得更奇怪了。这位管家长得又高又瘦，皮肤像橄榄一样黝黑，长鹰钩鼻上方的绿眼睛里仿佛跳动着一簇炽热的奇怪火苗。莫德注意到，他额头上方的黑发里似乎藏着两个对称的凸块，这让她不由得打了个冷战。

“要么我是在做梦，”她想道，“要么这就是从大剧院里走出来的墨菲斯托费勒斯^[5]本人了。”

“你是我丈夫雇来的吗？”她没话找话地大声问道。

“不完全是。”奇怪的管家一边继续布置餐桌，一边回答，“事实上，我来到这里是为了告诉您那位杰出的父亲，我并不像他认为的那样只存在于传说中。请允许我介绍一下自己。我就是麦克斯韦妖。”

“噢！”莫德松了口气，“那你应该不像别的妖怪那么邪恶吧，而且应该不会伤害任何人。”

“当然不会。”麦克斯韦妖露出灿烂的笑容，“但我很喜欢恶作剧，现在我就打算捉弄一下您的父亲。”

“你打算干什么？”莫德还是有些担心。

“要我来说的话，我只是想让他看看，熵增法则是可以被打破的。为了让你也相信这一点，我希望你能陪我一起去。我向你保证，绝不会有任何危险。”

听完这番话，莫德立即感觉到麦克斯韦妖紧紧抓住了自己的手腕，周围的一切突然变得古怪起来。餐厅里她熟悉的所有东西都开始飞速变大，她看到的最后一幕景象是一张椅子的椅背占据了她的整个视野。等到一切终于平静下来，她发现自己飘浮在空中，麦克斯韦妖小心地搀扶着她。无数网球大小、轮廓模糊的球体在她周围杂乱无章地飞舞，但麦克斯韦妖带着她灵活地躲开了所有飞舞的小球，她现在的确很安全。莫德一低头就看见了一艘类似渔船的容器，船舱里装满了银光闪烁的鱼儿。但那并不是鱼，而是无数个轮廓模糊的小球，看起来和空中飞舞的球体一模一样。麦克斯韦妖带着她继续向下，乱哄哄翻涌的小球就像一锅沸腾的糙米粥，毫无规律可循。有的球仿佛被什么力量推着一路上升，有的球颓然下沉。偶尔有一颗球高速冲向液面表层，速度快得仿佛足以撕裂空间，转眼又有一颗球扎进翻滚的“稀粥”深处，瞬间消失在无数同类下方。近距离观察这锅沸粥，莫德发现，小球实际上分为两种，其中大部分球体的尺寸都和网球差不多，但也有一些球体积更大，形状更扁，看起来就像美式橄榄球。所有球体都是半透明的，莫德隐约看见，它们的内部结构似乎相当复杂。

“我们这是在哪儿呀？”她倒吸一口凉气，“难道这就是地狱的模样？”

“不是啦，”麦克斯韦妖笑道，“没有那么异想天开。现在我们只是在极近的距离上观察高杯里的酒，正是靠着这杯酒，你丈夫才能强撑着听你父亲解释准遍历系统而不至于酣然入睡。你看到的球体都是分子。小的圆球是水分子，大的椭圆球是酒精分子。仔细观察一下它们的数量比，你就知道你丈夫喝的酒有多烈。”

“很有趣。”莫德努力让自己的口气显得严厉一点，“但水里还有一些看起来像是鲸的东西，它们该不会是原子世界里的鲸吧？”

麦克斯韦妖望向她指的方向。“喔，那不是鲸，”他说，“事实上，那只是一些烧焦的大麦碎片，正是这种物质赋予了威士忌独特的风味和颜色。每块碎片都由上亿个复杂的有机分子组成，所以相对于其他分子来说，它们显得又大又重。你看到这些碎片在酒杯里载浮载沉，这是因为它们正在不断经受热运动水分子和酒精分子的撞击。这些中等尺寸的碎片小得足以被分子运动影响，又大得能被高倍数显微镜观察到，正是通过对这类微粒的研究，科学家才第一次为热动力学理论找到了最直接的证据。通过测量液体中悬浮的这种小颗粒令人眼花缭乱的舞步——人们常常称之为‘布朗运动’——物理学家得到了分子动能的第一手信息。”

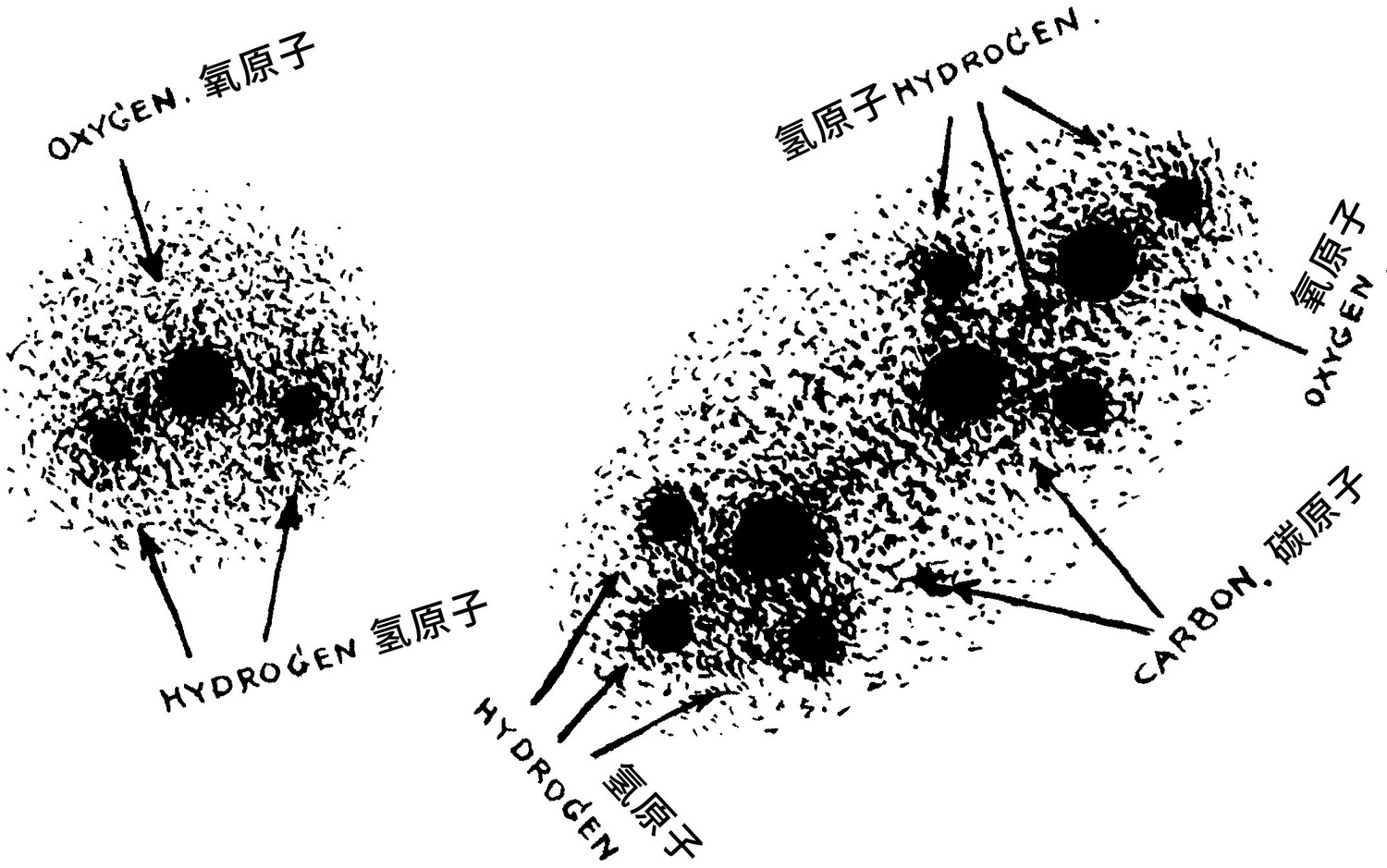
麦克斯韦妖再次搀着莫德在空中穿行，最后他们来到了一堵宏伟的高墙前面。这堵墙由无数像砖块一样排得密密麻麻、整整齐齐的水分子组成。

“真是太壮观了！”莫德赞叹道，“这正是我一直想要寻找的背景——我正在画一幅肖像。不过，这座漂亮的建筑到底是干什么的呀？”

“喔，这是冰晶的一部分，你丈夫酒杯里的冰块就是由很多这样的冰晶组成的。”麦克斯韦妖回答，“现在，请容我失陪片刻，我得去捉弄那位满怀自信的老教授了。”

他一边说，一边让莫德待在冰晶边缘，就像一位不太高兴的登山者一样，然后他开始捣乱了。他不知道从哪儿弄来了一个网球拍似的装置，用它来击打周围的分子。他灵活地左右腾挪，任何一个跑错了方向的分子都逃不过他的校正。尽管莫德现在待的位置不太安全，但她还是情不自禁地开始欣赏麦克斯韦妖敏捷的动作和准确的判断，每当他成功拦截了一个速度特别快的分子，她就激动得欢呼起来。麦克斯韦妖的表现如此精彩，相比之下，就连最杰出的网球冠军也显得迟钝而笨拙。短短几分钟内，他的努力就取得了显著的成果。现在，尽管液体表面部分区域的分子速度慢得近乎停滞，但她脚下的液面却比刚才活跃多了。通过蒸发过程从液体表面逃逸的分子数量正在飞速增加，巨大的气泡不断撕裂液面，一团团气体争先恐后地向上升腾，每个气体团里都有上千个分子。紧接着，蒸汽形成的云朵遮蔽了莫德的整个视野，她只能透过狂乱的分子偶尔瞥到球拍挥舞的一角，或者麦克斯韦妖那身燕尾服的尾巴。最后，组成冰晶的分子也开始变得不安分起来，她被晃得摔了出去，直直坠向下方厚厚的蒸汽云……

等到云层散尽，莫德发现自己好端端地坐在原来那把椅子里，仿佛根本没有起身去过餐厅。

“神圣的熵啊！”她的父亲望着汤普金斯先生手中的酒杯，惊讶地喊叫起来，“它在沸腾！”

杯子里的液体内部充满了疯狂沸腾的气泡，一缕蒸汽云正缓缓飘向天花板。眼前的景象看起来奇怪极了，因为实际上沸腾的只是冰块周围的一小片区域，杯子里剩余的部分还是一样冰冷。

“想想看吧！”教授声音因敬畏而颤抖起来，“刚才我还在给你讲熵定律的统计波动，现在我们就看到了一个实例！机缘巧合之下，运动速度较快的分子偶然聚集到液面上的一小块区域，杯子里的水自己沸腾起来！这可能是地球诞生以来的头一回！”

“哪怕再过几十亿年，恐怕也不会有第四个人有幸看到这非同寻常的一幕！”他紧盯着酒杯，现在杯子里的液体已经渐渐冷却下来。“我们真是太走运了！”他快活地叹道。莫德微笑起来，但她什么也没说。她不想和父亲争吵，但这一次她很有把握，她肯定比他知道得多。

[5]歌德名著《浮士德》里的魔鬼。