连续性微分方程在运动中的应用

对于三元直角坐标系，可以在流场中取一边长为δx、δy、δz的微小平行六面体为控制体积，如图3．17所示。其中心位于（x，y，z），中心x、y、z方向的流速分量分别为ux、uy、uz，密度为ρ。首先考虑垂直于x方向的一对控制表面（平面）的质量流量。因假定各处的ρ和ux为连续变化，故经右侧面流出的质量流量为式中，ρuxδyδz是垂直于x轴中间平面的质量流量。第二项是质量流量对x的变化率乘以到右侧面距离。同理，左侧面流入控制体积的质量流量应为

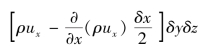
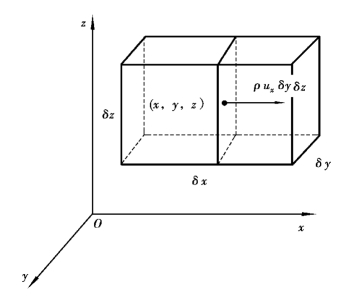
图3．17　直角坐标中推导三元流连续性方程的控制体

流出两平面的净质量流量为

对另两方向可得类似表达式，因此总净流出质量流量为

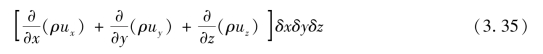
对于微元控制体积内，质量减少率应为

根据质量守恒定律，式（3．35）与式（3．36）应相等。令其相等后除以微元体积δxδyδz，并取极限，δx、δy、δz趋于零，于是对于一点的连续方程为

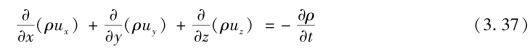
该式对恒定流、非恒定流、可压缩或不可压缩流动中任一点都适用。对不可压缩流动，可简化成

对恒定流，＝0，得

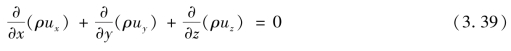(https://www.daowen.com)

式（3．37）、式（3．38）及式（3．39）可用矢量形式表达，式（3．37）写为

对不可压缩流：

对恒定流：

式中，点积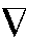·u称为流速矢u的散度，它的意义是一点处单位体积流出的净流量，对于不可压缩流动，它必然等于零。

对于二元流，一般假定流动平面同x、y平面平行，uz＝0，相对于z方向流动没有变化，因此，，其连续方程由简化三元流连续方程而得。

例3．4 二元不可压缩流的流速分布由下式表示，即

证明此流动满足连续性方程。

证明 由式（3．38），二元流的连续性方程为

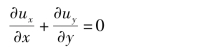
因

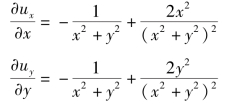
代入连续性方程，它们之和为0，故该流动满足连续性方程。