Goldschmidt在研究晶体结构时，结合以上几个影响因素提出了Goldschmidt结晶化学定律：一个晶体的结构取决于其组成单位的数量、相对大小和极化性质。在此基础上，1928年，Pauling根据对硅酸盐和含氧酸的研究提出了离子化合物结构的五条规则，即鲍林规则。（Pauling's rule）。

1.配位多面体规则

晶体结构中，每个阳离子周围的阴离子形成一个配位多面体；阴、阳离子之间的距离由它们的半径之和决定；阳离子的配位数由阴、阳离子的半径比决定。该规则表明阳离子的配位数取决于阴、阳离子的半径比，而并非它们本身的半径。图3.6示意了离子半径比与配位数的情况。当阴、阳离子刚好接触时是稳定的。若阳离子过小，阴、阳离子不能接触，阴离子之间的斥力使阳离子配位数下降；若阳离子过大，会撑开阴离子，阳离子配位数增加。由离子的刚性球模型，可以计算出阳离子在一定配位数时的阴、阳离子的半径比的临界值：

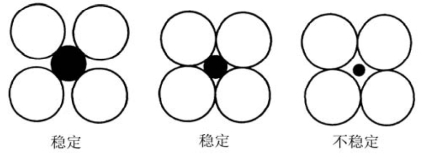
图3.6　稳定与不稳定配位构型（引自Kingery，2010）

r+/r-∈（0，0.155），阳离子配位数CN=2，配位多面体为直线或哑铃型；

r+/r-∈［0.155，0.225），阳离子配位数CN=3，配位多面体为等边三角形；

r+/r-∈［0.225，0.414），阳离子配位数CN=4，配位多面体为四面体；

r+/r-∈［0.414，0.732），阳离子配位数CN=6，配位多面体为八面体；

r+/r-∈［0.732，1），阳离子配位数CN=8，配位多面体为立方体；

r+/r-=1，阳离子配位数CN=12，等径球紧密堆积。

大多数离子晶体的阳离子配位数CN在4～8之间，而且还不是一个定值，如Al离子，有［AlO4］，也有［AlO6］。由于晶体结构受多种因素影响，实际晶体结构还会出现不符合这一规则的情况。特别是阴离子不做最紧密堆积时，阳离子配位数CN可以是5、7、9、11等。(www.daowen.com)

2.静电价规则

一个稳定的结构，不仅在宏观上是电中性，在原子尺度上也必须是电中性。该规则是计算局部电中性的基础。阳离子价电荷数Z除以其配位数CN得到的值定义为阳离子给予一个配位阴离子的静电键强度S，其中S=Z/CN。萤石CaF2，Ca2+的CN=8，即一个Ca2+周围有八个F-。一个Ca-F键的静电键强度S=+2/8=+1/4，即一个Ca2+分配到一个F-的电荷为+1/4。而F-的电荷为-1，故为保持电中性，一个F-周围需要有4个Ca2+。该规则指出：在稳定结构中，从所有最近邻阳离子到一个阴离子的静电键强度S的总和等于该阴离子电价。该规则对我们理解晶体结构有一定帮助。

如［SiO4］，Si4+给每个O2-的S=+4/4=+1，而O呈-2价，所以O2-还可与其他［SiO4］的Si4+或金属离子结合，如2个［SiO4］可共用1个O。在［AlO6］中，Al3+给O2-的S=+3/6=+1/2，故1个［SiO4］可与2个［AlO6］共用1个O，这两个［AlO6］称为二八面体。在［MgO6］中，Mg2+给O2-的S=+2/6=+1/3，故1个［SiO4］可与3个［MgO6］共用1个O，这三个［MgO6］称为三八面体。

3.配位多面体的连接方式

在一个配位结构中，两个阴离子配位多面体以共棱，特别是共面方式存在时，结构的稳定性降低。这种效应对于电价高而配位数小的阳离子（如Si4+）较明显。当阴、阳离子的半径比接近该配位多面体稳定的下限值时，此效应更显著。多面体共棱，特别是共面时，中心阳离子相距较近，斥力大，结构很不稳定。以四面体为例，图3.7（a）表示四个四面体分别共A、B、C、D四个顶点；图3.7（b）表示两个四面体共AB棱；图3.7（c）表示两个四面体共ABC面。在硅酸盐结构中，［SiO4］只能共顶，而［AlO6］可以共棱。刚玉结构中的［AlO6］还可共面。

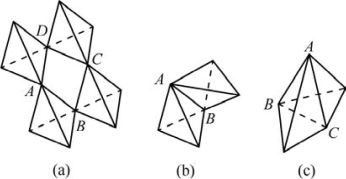
图3.7　四面体共顶、共棱、共面示意图（引自Askeland，2005）

4.不同配位多面体的连接

在一个含有不同阳离子的晶体中，电价高而配位数小的那些阳离子，不趋向于相互共有配位多面体的要素。这条规则是第三条规则的延伸。所谓共有配位多面体的要素，是指共顶、共棱和共面。如果在一种晶体结构中，有多种阳离子存在，则高电价、低配位数阳离子的配位多面体趋向于尽可能互不相连，至多也只能以共顶方式相连，如橄榄石结构有［SiO4］和［MgO6］。Si4+电价高、配位数低，因此［SiO4］彼此之间无连接，它们由［MgO6］隔开。

5.节约规则

在一个晶体中，本质不同的结构组元，其种类趋向于为数最少，此规则称为节约规则。例如在硅酸盐晶体结构中，不会同时出现［SiO4］四面体和［Si2O7］双四面体结构基元，尽管它们符合鲍林其他四条规则。第五条规则是由晶体结构的周期性和对称性决定的。如果组成晶体结构的基元较多，每一种基元都要形成自己的周期性、对称性，则它们之间会相互干扰。这不利于晶体结构的形成。

鲍林规则是由离子晶体结构归纳出来的。它符合大多数离子晶体的结构情况。但它不完全适用于过渡元素的离子晶体，更不适合非离子晶格的晶体。过渡元素的离子晶体和非离子晶格的晶体需要用晶体场、配位场理论来说明。