浓度计算三角形法则

虽然三元相图比较复杂，但它与单元、二元相图一样也是有规律可循的。掌握下面一些规则有利于对三元相图进行分析。

1.等质量分数（或摩尔分数、原子分数）规则

在浓度三角形中，平行于三角形一条边的直线上的所有系统组成点，其对面顶点组元的质量分数相等。如图8.80（a）所示，设HK平行于AB，则HK上所有状态点的C质量分数相等。以该直线上的任意两点M、N为例来做一简单证明。

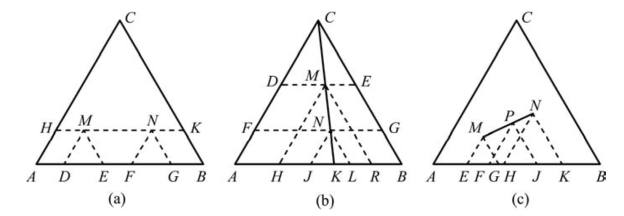
图8.80　（a）等质量分数规则；（b）等比例规则；（c）杠杆规则

根据图8.79获得浓度三角形中任意一点组成的表示方法，分别过M、N点作AC、BC边的平行线DM、EM、FN、GN。M点系统中，C的质量分数为DE段；N点系统中，C的质量分数为FG段。可以证明△DEM和△FGN不仅全等且都是正三角形，所以DE=FG，即任意M、N点系统，它们对应C的质量分数相等。

2.等比例规则

从浓度三角形顶点向对边作射线，射线上所有系统组成点含有对边两个组分的质量分数之比恒定。如图8.80（b）所示，从C向对边AB作任一射线CK，则CK上所有系统组成点含有A、B的质量分数之比恒定。

以射线CK上的任意两点M、N为例。为获得M点的组成，过M点作AB、BC和CA的平行线DE、MR、MH；过N点作AB、BC和CA的平行线FG、NL、NJ。M点系统中，A、B的质量分数分别为BR、AH，质量分数之比为BR/AH。因BRME和AHMD是平行四边形，故BR=ME，AH=DM，所以M点系统中，A、B的质量分数之比为ME/DM。同理，N点系统中，A、B的质量分数之比为NG/FN。

因为△CDM∽△CAK，所以DM/AK=CM/CK。又因为△CME∽△CKB，所以CM/CK=ME/BK。由以上两个等式得DM/AK=ME/BK，变形后得ME/DM=BK/AK。同理，对N点系统，也有A、B的质量分数之比NG/FN=BK/AK，故射线上任意的M、N点含对边A、B的质量分数之比相等。

3.背向性规则

在浓度三角形中，一个三元系统的组成点与某个顶点相距越远，则该系统含有越少的顶点组元。图8.80（b）中的M、N点，其中N点与顶点C的距离大于M与C的距离。因此，N点系统中C的质量分数比M点系统小。当组成点达到AB边上时，系统不含C组分。(https://www.daowen.com)

4.杠杆规则

与二元相图一样，杠杆规则在三元系统中也非常重要。这个规则有两层含义：一是在三元系统内，由两个相（或混合物）组成一个新相（或新混合物）时，新相（或新混合物）的组成点必在原来两相（或混合物）组成点的连线上。如图8.80（c）所示，M、N点系统组成一个新系统P，P点必在MN线上，且M、N在P点两侧。反之，P点系统由一相分解为两相时，这两相的组成点M、N必分布在P点两侧，且这三点也在同一直线上。有些文献称这为直线规则。

杠杆规则的另一层含义与二元系统相同。图8.80（c）中，M、N点系统组成一个新系统P。设M、N点系统的质量分别是m、n。过M、N、P点作AC、BC边的平行线，获得各点组成。以A组元做质量衡算。M系统中A的质量分数为BG。N系统中A的质量分数为BK。P系统中A的质量分数为BJ。M、N两个系统中A的质量之和等于P系统中A的质量，所以mBG+nBK=（m+n）BJ。整理后得m/n=JK/GJ。

又因为MG∥PJ∥NK，MN、GK是这三条平行线的截线。根据平行线分线段成比例定理，JK/GJ=PN/MP，故m/n=PN/MP。这与二元系统中式（8-14）一致。

5.重心规则

三元系统在达成四相平衡时，这四相的组成点位置可能存在三种关系。

（1）重心位置，如图8.81（a）所示。设M、N、Q三相合成新相P。根据杠杆规则，N、Q系统组成的S点在NQ线上，简写为N+Q=S。同样，根据杠杆规则，S点与M点系统合成新系统P，则S+M=P。因此，P的组成点必在△MNQ内。上述过程可简写为M+N+Q=P（读者需注意，此处的重心位仅表示新相P处于△MNQ内，而不是P点一定是在△MNQ的几何重心位）。

（2）交叉位置，如图8.81（b）所示。新相P的组成点在三角形的一条边NQ外侧，且在另两条边（MQ、MN）的延长线所夹范围内。连接MP交NQ于S。由杠杆规则N+Q=S、M+P=S。整理后有P=N+Q-M，此式表明N、Q两相要回吸M相才能获得新相P，即要发生转熔过程。

（3）共轭位置，如图8.81（c）所示。新相P的组成点在三角形的一个顶点Q外侧，且在形成此顶点的两条边（MQ、NQ）的延长线所夹范围内。连接P、Q并延长与MN交于S，同样有P+S=Q、M+N=S，整理得P+M+N=Q，此式表明，P、M、N三相可合成Q相。实际上，Q点在△MNP重心位。P+M+N=Q还可整理为P=Q-M-N，这表明Q相要回吸M、N相才能获得新相P，即要发生转熔过程，而且要转熔（或回吸）两相。

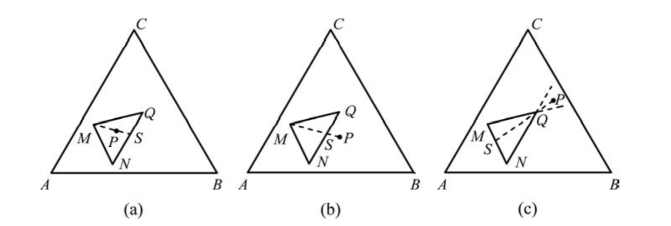
图8.81　（a）重心位置；（b）交叉位置；（c）共轭位置

以上这些规则在三元系统中适用于任意三角形，如图8.81中△MNQ属任意三角形。我们将在下文陆续介绍这些规则在三元相图中的应用。