【摘要】：定义B-6随机变量X的取值的统计平均我们用均值E[X]来表示，具体为有限情况（B-5）或者E[X]=∫xfdx无限情况（B-6）均值也被称做期望。相对于统计平均，我们都知道还有算术平均，算术平均是最早接触的平均概念了。几个数值的算术平均就是它们的和与它们总个数的比值。，N-1，它们的算术平均为显然，如果xi出现的概率相同，都为1/N，则统计平均等于算术平均。对于连续情况f，子≤x≤子+T求所有f的算术平均。
定义B-6（均值（Expectation））随机变量X的取值的统计平均我们用均值E[X]来表示，具体为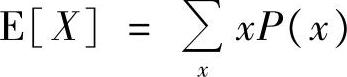
有限情况（B-5）
或者
E[X]=∫xf（x）dx无限情况（B-6）
均值也被称做期望。
相对于统计平均，我们都知道还有算术平均，算术平均是最早接触的平均概念了。几个数值的算术平均就是它们的和与它们总个数的比值。具体地，对于离散情况，假设有N个数xi，i=0，…，N-1，它们的算术平均为
显然，如果xi出现的概率相同，都为1/N，则统计平均等于算术平均。对于连续情况
f（x），子≤x≤子+T(https://www.daowen.com)
求所有f（x）的算术平均。和离散情况类似，先按离散情况依样画瓢把形式写出来。我们一步步来，先不求所有x∈[子，子+T]上的f（t）的算术平均，而是求[子，子+T]上间隔为△t的那些f（t）的算术平均，这个算术平均为
显然，当△t→0时，子+n△t可以覆盖整个区间[子，子+T]，也即所有f（t）的算术平均为
定义B-7（方差（Variance））一个随机变量X与它均值E[x]的平均距离，我们用方差Var[X]来表示，即
Var[X]=E[（X-E[X]）2]（B-9）
说明一下，可以证明E[X]是与随机变量X的取值平均距离最小的，并且这个最小值就是X的方差，即
留做练习吧，有兴趣的同学自己动手应用前面讲过的极值求解方法推导证明一下。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
