水文及水利水电随机变量的统计参数

从统计数学的观点来看，随机变量的概率分布曲线或分布函数较完整地描述了随机现象，知道了随机变量的概率分布函数或者概率密度函数，就掌握了随机变量在各个取值区间的概率，也就掌握了随机变量的统计规律。然而在许多实际问题中，随机变量的分布函数或者概率密度函数往往不易确定，或有时不一定都需要用完整的形式来说明随机变量，而只要知道概率分布某些具有特征意义的数值，可以简明地表示随机变量的统计规律和特性就够了。在概率论里，把这些数字称为随机变量的数字特征，在工程水文中，习惯于把这些数字称为统计参数。例如，某地的年降水量是一个随机变量，各年的降水量不同，具有一定的概率分布曲线，若要了解该地年降水量的概括情况，就可以用多年平均年降水量这个数量指标来反映。这种能说明随机变量统计规律的数字特征，称为随机变量的统计参数。水文现象的统计参数反映其基本的统计规律，能概括水文现象的基本特征和分布特点，也是频率曲线估计的基础。

统计参数有总体统计参数与样本统计参数之分。所谓总体是指某随机变量所有取值的全体，把总体中的每一个基本单位称为个体。如一条河流，当我们研究年径流量的时候，河流有史以来各年年径流量的全体就是总体，每年的年径流量就是个体。如果所研究的随机事物对应着实数，则总体就是一个随机变量（可以记为X），而个体就是随机变量的一个取值（可以记为xi）。一般情况下，总体是未知的。或者，因为不能对总体进行普查研究，总体实际上是无法得到。比如，我们无法掌握一条河流在其形成以来漫长时期内所有年份的年径流量。我们也不能对工地上所有的钢筋都进行破坏性试验来检验钢筋的强度。为了了解和掌握总体的统计规律，通常是从总体中抽取一部分个体，对这部分个体进行观察和研究，并且由这部分个体对总体进行推断，从而掌握总体的性质和规律。从总体中任意抽取的部分个体称为样本，样本中所包括的项数则称为样本容量。水文现象的总体通常是无限的，它是指自古迄今以至未来所有的水文系列，现有的水文观测资料可以认为是水文变量总体的随机样本。显然，水文随机变量的总体是不知道的，只能靠有限的样本观测资料去估计总体的统计参数或总体的分布规律，即由样本统计参数来估计总体统计参数。水文计算中常用的样本统计参数有均值、均方差、变差系数和偏态系数等。

1.均值

均值又称为期望，它表示随机变量平均数的概念。设某水文变量的观测系列（样本）为x1，x2，…，xn，则其均值为：

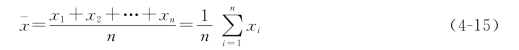
均值表示系列中变量的平均情况，可以说明这一系列总水平的高低。例如，甲河多年平均流量为2460m3/s，乙河多年平均流量为260m3/s，说明甲河流域的水资源比乙河流域丰富。均值不仅是频率曲线方程中一个重要参数，而且是水文现象的一个重要特征值。

令，则：

Ki称为模比系数，模比系数组成的系列，其均值等于1。这是水文统计中的一个重要特征。对于以模比系数所表示的随机变量，在其频率曲线方程中可以减少一个均值参数。

2.均方差

均值能反映系列中各变量的平均情况，但不能反映系列中各变量的集中或离散程度。例如，有两个系列：

第一系列：49，50，51；

第二系列：1，50，99。

这两个系列的均值相同，都等于50，但二者离散程度很不相同。直观地看，第一系列只变化于49～51之间，而第二系列的变化范围则增大到1～99之间。

研究系列中各变量集中或离散的程度，是以均值为中心来考查的。离散特征参数可用相对于分布中心的离差来计算。但离差有正有负，其平均值为零。为了使离差的正值和负值不致相互抵消，一般取的平均值的开方表示离散程度的大小，称为均方差，即：

如果系列的均值相等，则σ越大表示系列分布越离散，σ越小表示系列分布越集中。按式（4-17）计算上述两个系列的均方差为σ1=0.82，σ2=40.0。显然，第一系列的离散程度小，第二系列的离散程度大。

3.变差系数

均方差虽然能说明系列的离散程度，但对于均值不同的两个系列，则不能用均方差直接比较系列的离散程度。例如，有两个系列：

第一系列：5，10，15，；

第二系列：995，1000，1005，。

按式（4-17）计算上述两个系列的均方差都等于4.08，说明这两个系列的绝对离散程度是相同的，但它们对均值的相对离散程度就很不相同了。可以看出，第一系列中的最大值和最小值与均值之差都是5，这相当于均值的5/10=1/2；而在第二系列中的最大值和最小值与均值之差虽然也都是5，但只相当于均值的5/1000=1/200，在近似计算中，这种差距甚至可以忽略不计。

为了克服以均方差衡量系列离散程度的这种缺点，水文计算中用均方差与均值之比作为衡量系列的相对离散程度的一个参数，称为变差系数，或称离差系数、离势系数，用CV表示。变差系数为一无因次的小数，CV也可以理解为变量x换算成模比系数K以后的均方差。其计算式为：

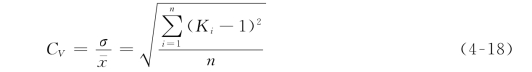
均方差和变差系数都表示随机变量的离散情况，但均方差和随机变量取值的大小有关，而变差系数是一个无因次的量，排除了随机变量自身大小的影响。

变差系数CV越大，表示系列的离散程度越大；CV越小，系列的离散程度则越小。按式（4-18）计算上述两个系列的变差系数CV1=0.408，CV2=0.00408，可见第一系列的离散程度明显大于第二系列。

CV是水文统计中常用的一个重要参数，用来说明水文特征值的变化情况。我国年降雨量和年径流量的CV值存在明显的地理分布规律，即南方大于北方，内陆大于沿海，山区大于平原。此外，CV还与流域的大小和流域形状有关，一般是大流域CV值比小流域要小，狭长流域的CV值比枝状流域要大。现有的CV等值线图可供水文工作者查用。(https://www.daowen.com)

4.偏态系数（偏差系数）

变差系数只能反映系列的离散程度，而不能反映系列在均值两边的对称程度。在水文统计中采用偏态系数CS作为衡量系列在均值两边对称程度的参数，其计算式为：

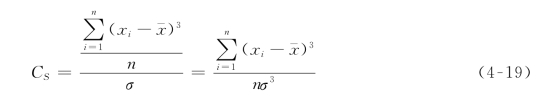
将式（4-19）右端的分子、分母同除以，则得：

CS值的大小可以反映频率分布的不对称程度，是一个无因次量。通常CS的绝对值越大，频率分布曲线越不对称；相反，如果CS的绝对值越小，频率分布曲线就越接近于对称。当系列对于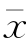对称时，CS=0，称为对称分布（或正态分布）；当系列对于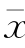不对称时，CS≠0，当正离差的立方占优势时，CS＞0，称为正偏分布；当负离差的立方占优势时，CS＜0，称为负偏分布。CS对密度曲线的影响如图4-3所示。

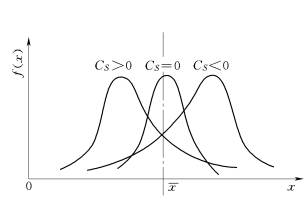
图4-3　CS对密度曲线的影响

水文现象大多属于正偏分布，即水文变量取值大于均值的机会比取值小于均值的机会少。当资料的项数不多时，计算出来的CS值误差很大。一般认为，资料在100项以下，CS是不能用公式计算的。因为短系列资料，离均差有误差，立方后误差更大，尤其是极端项影响更大。在实际工作中一般采用经验性的方法，比如取CS等于若干倍的CV。如年降雨量或年径流量的计算，常用CS=2CV的关系，对于年最大流量与年最大降雨量通常取CS等于3～4倍的CV。

5.矩

矩的概念及其计算在工程水文计算中经常遇到。矩在统计学中常用来描述随机变量的分布特征，均值等统计参数，有些可以用矩来表示。矩可分为原点矩和中心矩两种。

（1）原点矩。随机变量X所能取的一切可能值以其相应的概率（或概率密度）为权的加权平均数，称为随机变量X的数学期望，记为E（X）。随机变量X对原点离差的r次幂的数学期望E（Xr），称为随机变量X的r阶原点矩，以符号mr表示，即：

对离散型随机变量，r阶原点矩为：

对连续型随机变量，r阶原点矩为：

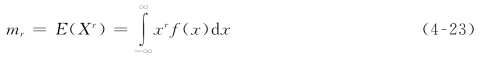
当r=1时，，即一阶原点矩就是数学期望，也就是算术平均数（均值）。

（2）中心矩。随机变量X对分布中心E（X）离差的r次幂的数学期望E{[XE（X）]r}，称为随机变量X的r阶中心矩，以符号μr表示，即：

对离散型随机变量，r阶中心矩为：

对连续型随机变量，r阶中心矩为：

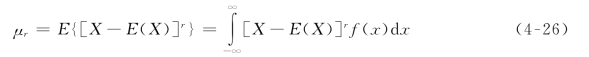
当r=2时，μ2=E{[X-E（X）]2}=σ2，由式（4-17）可知，随机变量的二阶中心矩就是标准差的平方（称为方差）。

当r=3时，μ3=E{[X-E（X）]3}，由式（4-19）可知，Cs=μ3/σ3。

综上所述，均值、变差系数和偏态系数都可以用各种矩表示。