1.空间向量及其加减与数乘运算
(1)在空间,具有大小和方向的量叫作向量.长度相等且方向相同的有向线段表示同一向量或相等的向量.
(2)空间向量的加法、减法与向量数乘运算是平面向量运算的推广.
(3)空间向量的加减与数乘运算满足如下运算律.
加法交换律![]()
加法结合律![]()
数乘分配律![]()
2.共线向量与共面向量
(1)如果表示向量的有向线段所在的直线互相平行或重合,则这些向量叫共线向量或平行向量.
(2)平行于同一平面的向量叫作共面的向量.任意两个向量总是共面的.
(3)共线向量定理:对空间任意两个向量![]() 的充要条件是存在实数λ使
的充要条件是存在实数λ使![]()
推论:如果l为经过已知点A且平行于已知非零向量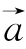 的直线,那么对任一点O,点P在直线l上的充要条件是存在实数t,满足等式
的直线,那么对任一点O,点P在直线l上的充要条件是存在实数t,满足等式![]() .其中向量
.其中向量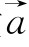 叫作直线l的方向向量.
叫作直线l的方向向量.
(4)共面向量定理:如果两个向量![]() 不共线,则向量
不共线,则向量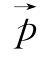 与向量
与向量![]() 共面的充要条件是存在实数对x,y,使
共面的充要条件是存在实数对x,y,使![]()
推论:空间一点P位于平面MAB内的充要条件是存在有序实数对x,y,使![]()
![]() 或对空间任一定点O,有
或对空间任一定点O,有![]()
方法简述
基本定义法
例1 在下列命题中:
①若向量![]() 共线,则向量
共线,则向量![]() 所在的直线平行;
所在的直线平行;
③若三个向量![]() 两两共面,则向量
两两共面,则向量![]() 共面;
共面;
④已知空间的三个向量![]() ,则对于空间的任意一个向量
,则对于空间的任意一个向量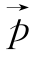 ,总存在实数x,y,z使得
,总存在实数x,y,z使得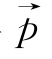
![]()
其中正确命题的个数是( ).
A.0 B.1 C.2 D.3
解答 A
反思 多举反例.
例2 在空间四边形ABCD中![]() =( ).
=( ).
A.-1 B.0 C.1 D.不确定
例2答图
点拨 解法一:如图所示,在空间四边形ABCD中,联结对角线AC,BD,得三棱锥A-BCD,不妨令其各棱长都相等,即为正四面体.
∵正四面体的对棱互相垂直,
解法二:在解法一的图中,选取不共面的向量![]() 为基底,
为基底,
解答 B
反思 几何法以及基向量法都可以解答.
例3 若![]() 为空间的一组基底,则下列各项中,能构成基底的一组向量是( ).
为空间的一组基底,则下列各项中,能构成基底的一组向量是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
点拨 若![]() 共面,则
共面,则![]() 为共面向量,此与
为共面向量,此与![]() 为空间向量的一组基底矛盾,故
为空间向量的一组基底矛盾,故![]() 可构成空间向量的一组基底.
可构成空间向量的一组基底.
解答 C
反思 理解基向量的意义.
例4 在下列条件中,使M与A,B,C一定共面的是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
点拨 对共面的理解.
∵![]() ,则
,则![]() 为共面向量,即M,A,B,C四点共面.
为共面向量,即M,A,B,C四点共面.
解答 C
反思 注意向量的运算技巧.
例5 已知O是空间中任意一点,A,B,C,D四点满足任意三点不共线,但四点共面,且![]() ,则2x+3y+4z=________.
,则2x+3y+4z=________.
点拨 ∵A,B,C,D四点共面,
∴![]() ,且m+n+p=1.
,且m+n+p=1.
由条件知![]()
∴(-2x)+(-3y)+(-4z)=1.(https://www.daowen.com)
∴2x+3y+4z=-1.
解答 -1
反思 对四点共面的向量转化.
例6图
例6 已知在一个60°的二面角的棱上,如图所示,有两个点A和B,AC,BD分别是在这个二面角的两个半平面内垂直于AB的线段,且AB=4厘米,AC=6厘米,BD=8厘米,则CD的长为_______.
点拨 设![]()
由已知条件知![]()
则![]() 厘米.
厘米.
解答 ![]() 厘米
厘米
反思 向量模的运算技巧.
例7图
易错解读
例7 如图所示,在空间四边形OABC中,OA=8,AB=6,AC=4,BC=5,∠OAC=45°,∠OAB=60°,则OA与BC所成角的余弦值等于_______.
解答 设![]() 与BC所成的角为θ.
与BC所成的角为θ.
∴![]()
![]()
∴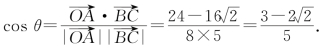
易错分析 如何选取正确的基向量是关键.
例8图
例8 如图所示,在平行六面体ABCD-A1B1C1D1中G为△A1BD的重心,设![]() ,试用
,试用![]() 表示
表示![]()
易错分析 (1)通过以上表示可以看出![]() ,即证明A,G,C1三点共线.G为AC1的三分之一分点.
,即证明A,G,C1三点共线.G为AC1的三分之一分点.
(2)解决几何问题的难点是作辅助线,而利用向量解决几何问题恰好回避了这一难点问题,把证明转化为运算.
例9图
例9 如图所示,已知平行六面体ABCD-A'B'C'D',E,F,G,H分别是棱A'D',D'C',C'C和AB的中点,求证:E,F,G,H四点共面.
所以![]() 共面.即E,F,G,H四点共面.
共面.即E,F,G,H四点共面.
易错分析 证明E,F,G,H四点共面,只需证明![]() 即可,即证
即可,即证![]()
![]() 三个向量共面.此种方法也是证明直线与平面平行的方法.
三个向量共面.此种方法也是证明直线与平面平行的方法.
经典训练
1.有以下命题:①如果向量![]() 与任何向量不能构成空间向量的一组基底,那么
与任何向量不能构成空间向量的一组基底,那么![]() 的关系是不共线;②O,A,B,C为空间四点,且向量
的关系是不共线;②O,A,B,C为空间四点,且向量![]() 不构成空间的一个基底,那么点O,A,B,C一定共面;③已知向量
不构成空间的一个基底,那么点O,A,B,C一定共面;③已知向量![]() 是空间的一个基底,则向量
是空间的一个基底,则向量![]() 也是空间的一个基底.其中正确的命题是( ).
也是空间的一个基底.其中正确的命题是( ).
A.①② B.①③
C.②③ D.①②③
2.如图所示,在平行六面体ABCD-A1B1C1D1中,M为A1C1与B1D1的交点.若![]()
![]() ,则下列向量中与
,则下列向量中与![]() 相等的向量是( ).
相等的向量是( ).
第2题图
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.已知A(1,2,3),B(2,1,2),P(1,1,2),点Q在直线OP上运动,当![]() 取最小值时,点Q的坐标是________.
取最小值时,点Q的坐标是________.
4.设![]() ,且
,且![]() ,则xy=_______.
,则xy=_______.
5.已知向量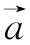 =(0,-1,1)
=(0,-1,1)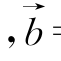 =(4,1,0),
=(4,1,0),![]() 且λ>0,则λ=_________.
且λ>0,则λ=_________.
6.在直角坐标系xOy中,设A(-2,3),B(3,-2),沿x轴把直角坐标平面折成大小为θ的二面角后,这时![]() ,则θ的大小为________.
,则θ的大小为________.
第7题图
7.如图所示,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=![]() ,则B1到平面PAD的距离为________.
,则B1到平面PAD的距离为________.
8.已知![]() ,且
,且![]() 不共面,若
不共面,若![]() ,求x,y的值.
,求x,y的值.
9.已知空间三点A(-2,0,2),B(-1,1,2),C(-3,0,4),设![]()
(1)求 与
与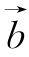 的夹角θ的余弦值;
的夹角θ的余弦值;
(2)若向量![]() 互相垂直,求k的值.
互相垂直,求k的值.
10.已知空间三点A(0,2,3),B(-2,1,6),C(1,-1,5).
(1)求以向量![]() 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;
(2)若向量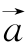 分别与向量
分别与向量![]() 垂直,且
垂直,且![]() ,求向量
,求向量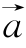 的坐标.
的坐标.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







