双真向量与条件闭合差之间的关系

因为在典型图形中总是有一条边的高差真值是已知的，在求解其余各边的真值时，都是先求出其对边的高差真值，然后再求解其余各伴随边的真值，下面将讨论在双真向量情况下，也就是说由一真向量变成双真向量时，它们所对应的两个再生误差与条件方程闭合差之间存在的关系。

式中各条件与(5-27a)式中的相应条件相减，并顾及误差距的定义，则可得到以下各式:

将(5-29)式中的第1、2两式以及第3、4两式分别相加，即可得到以下两式:

再将(5-30)式中两式分别相加和相减，即可得到以下两式:

则有原条件和再生条件为:

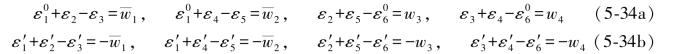
由对应的两个条件相减，得

将上述第1、2两式以及第3、4两式分别相加得

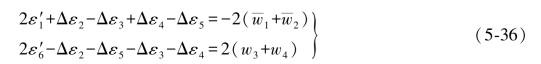
再将(5-36)式中两式相加和相减，得

则条件方程及其再生条件方程为:

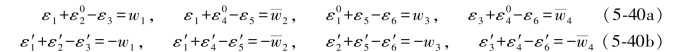
对应相减即可写出以下各式:

由上述第1、3两个条件以及第2、4两个条件分别相加得:

再将(5-42)中两式相加和相减，即可得到以下两式:

则条件方程及其再生条件方程为:

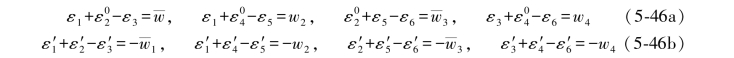
由(5-46a)式与(5-46b)式相减可得

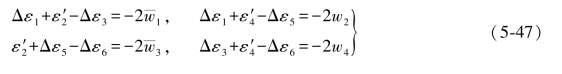
将(5-47)式的第1、3两式和第2、4两式分别相加得

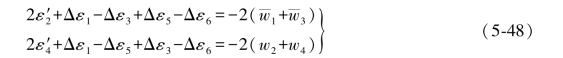
再将(5-48)式中两式相加和相减即得

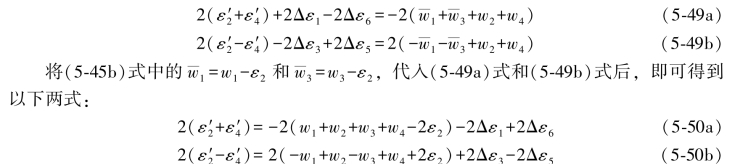
(5-43)和(5-49)两式中的和应该是相等的。

则其条件方程以及再生条件方程为:

将以上各式对应相减得

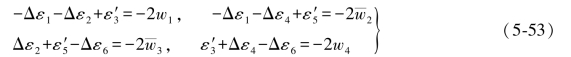
将(5-53)式中的第1、4两式以及第2、3两式分别相加得

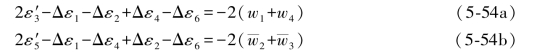
将(5-54a)式与(5-54b)式相加和相减即得

由(5-58a)式和(5-58b)式可以写出:

将其中第1、4两式和第2、3两式分别相加得

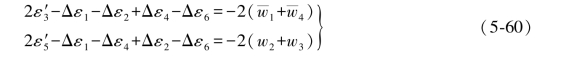
再由以上两式相加和相减，即得

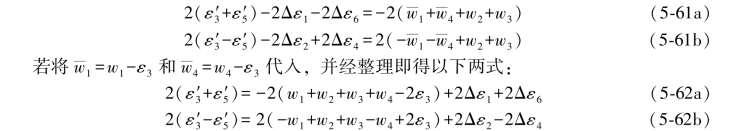(https://www.daowen.com)

(5-62a)式和(5-62b)式中的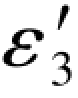和应该和(5-56)式中的相等。

以上导出了互为对边的再生误差之和或差同条件方程闭合差以及误差距之间的函数关系。

【例题1续5】由于推导方法相同，图形F的相关公式只写出其结果。

①互为对边的综合误差之和与差(用图F的综合误差公式见表1.5):

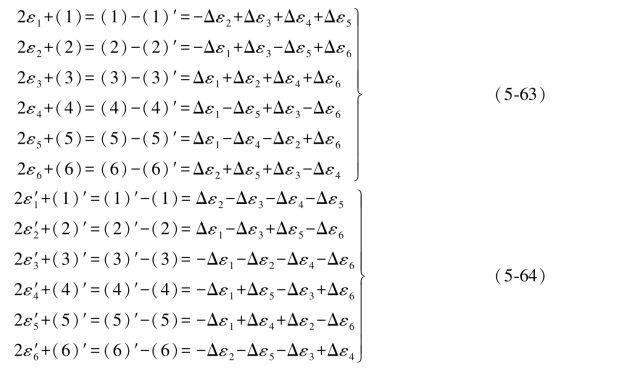
②从表1.4中可以查到图形F的误差距，互为对边的误差距之和与差为:

③在双真向量情况下，其再生真误差与条件闭合差之间的关系。

由上述条件与其再生条件方程相减可得(具体推导省略):

将以上第1、2两式以及第3、4两式分别相加，得

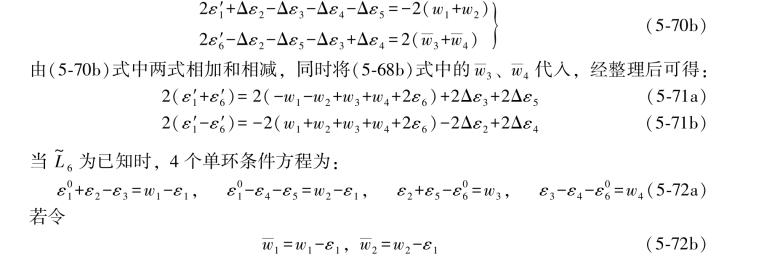
则条件方程应为:

与其相应的再生条件方程相减，即可得到以下各式:

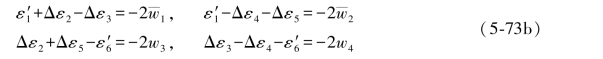
由以上第1、2两式和第3、4两式分别相加，得

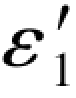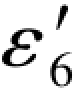(5-71)式和(5-75a)与(5-75b)两式中的和应相等。

则条件方程应为:

以上条件与其相应的再个条件相减可得以下各式:

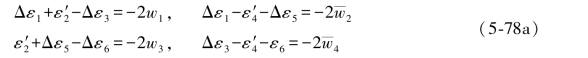
将上述4式中的第1、3两式以及第2、4两式分别相加，得

则可写出

(5-81a)式中各式与其相应的再生条件相减，即得

将(5-81a)式中的第1、3两式以及第2、4两式分别相加，则有:

于是(5-83a)式即可写成如下形式:

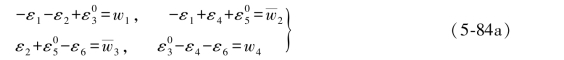
(5-84a)式中各式与其相应的再生条件相减即可得到以下各式:

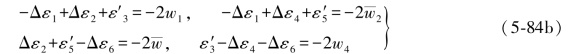
将(5-84b)式中的第1、4两式以及第2、3两式分别相加，即得

则条件式可以写成如下形式:

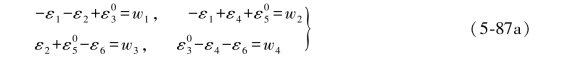
(5-87a)式与其相应的再生条件相减，即可得到以下各式:

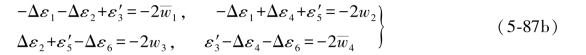
将(5-87b)式中的第1、4两式以及第2、3两式分别相加，则有

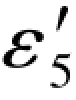(5-85)式和(5-89)式中的和应相等。

图形H的所有条件方程都与图形D的相同，只是闭合差数值不同，因此有关图形H的公式就不再另行给出。